【交流発電機の誘導起電力】『大きさ』と『向き』について解説！

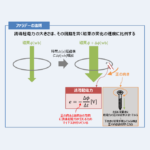
一様な磁束密度の中でコイルを回転させると、コイルを貫く磁束が変化することで、誘導起電力が発生します。

この記事では、この誘導起電力の大きさ、向き、例題について図を用いて説明しています。

交流発電機の誘導起電力の大きさ

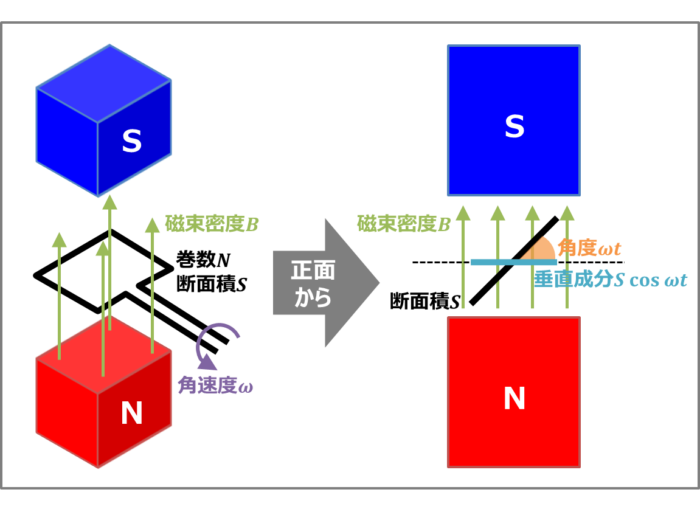
上図に一様な磁束密度\(B{\mathrm{[T]}}\)の中で、巻数\(N\)、断面積\(S{\mathrm{[m^2]}}\)のコイルが角速度\({\omega}{\mathrm{[rad/s]}}\)で回転している様子を示しています。

時刻\(t{\mathrm{[s]}}\)においては、コイル面と磁束密度\(B{\mathrm{[T]}}\)のなす角は\({\omega}t{\mathrm{[rad]}}\)となります。その時、コイルを垂直に貫く磁束\({\phi}{\mathrm{[wb]}}\)の成分は次式で表されます。

\begin{eqnarray}
{\phi}=BS{\cos}{\omega}t{\mathrm{[wb]}}\tag{1}
\end{eqnarray}

コイルの巻数は\(N\)なので、(1)式を用いると、コイルの磁束鎖交数\({\psi}{\mathrm{[wb]}}\)は次式となります。

\begin{eqnarray}
{\psi}=N{\phi}=NBS{\cos}{\omega}t{\mathrm{[wb]}}\tag{2}
\end{eqnarray}

従って、コイルの誘導起電力\(e{\mathrm{[V]}}\)はファラデーの法則を用いると次式で表されます。

\begin{eqnarray}
e=-\frac{d{\psi}}{dt}=-\frac{d}{dt}\left(NBS{\cos}{\omega}t\right)=N{\omega}BS{\sin}{\omega}t{\mathrm{[V]}}\tag{3}
\end{eqnarray}

(3)式の誘導起電力の式には『\({\sin}\)』があります。そのため、コイルに誘導される起電力\(e{\mathrm{[V]}}\)は正弦波状に変化するということになります。このような電圧を交流電圧といいます。また、交流電圧を抵抗に加えたときに流れる電流を交流電流または交流(AC:Alternating Current)といいます。

ここで、『\(E_{M}=NωBS\)』と置くと、(3)式は次式となります。

\begin{eqnarray}
e&=&N{\omega}BS{\sin}{\omega}t\\
&=&E_{M}{\sin}{\omega}t{\mathrm{[V]}}\tag{4}
\end{eqnarray}

(4)式より、コイルの誘導起電力\(e{\mathrm{[V]}}\)は、コイルの巻数\(N\)、角速度\({\omega}{\mathrm{[rad/s]}}\)、断面積S{\mathrm{[m^2]}}、磁束密度\(B{\mathrm{[T]}}\)が大きいほど、大きくなることが分かります。

なお、交流電圧は、上式の振幅\(E_{M}\)の代わりに実効値を用いることがあります。実効値\(E_{RMS}\)を用いると(4)式は次式となります。

\begin{eqnarray}
e&=&E_{M}{\sin}{\omega}t\\
&=&\sqrt{2}E_{RMS}{\sin}{\omega}t{\mathrm{[V]}}\tag{5}
\end{eqnarray}

ファラデーの法則とは

ファラデーの法則とは、「電磁誘導によって生じる誘導起電力の大きさは、その回路を貫く磁束の変化の速度に比例する」ことを表した法則です。詳しくは以下の記事に説明していますので、参考にしてください。

: 【ファラデーの法則とは？】『公式』や『積分形』や『微分形』などを詳しく解説！
続きを見る

【補足】角速度、周期、周波数の関係

周期

コイルが1回転するに要する時間です。記号は\(T\)、単位は\({\mathrm{[s]}}\)となります。

周波数

コイルが1秒間に回転する回数です。記号は\(f\)、単位は\({\mathrm{[Hz]}}\)となります。

角速度

コイルが1秒間に回転する角度です。記号は\({\omega}\)、単位は\({\mathrm{[rad/s]}}\)となります。

周期\(T{\mathrm{[s]}}\)、周波数\(f{\mathrm{[Hz]}}\)、角速度\({\omega}{\mathrm{[rad/s]}}\)には以下の関係式があります。

\begin{eqnarray}
T=\frac{1}{f}=\frac{2{\pi}}{{\omega}}\tag{6}
\end{eqnarray}

例えば、コイルが1回転するのに要する時間(周期)が\(T=0.1{\mathrm{[s]}}\)だとすると、1秒間に回転する回数(周波数)は\(f=10{\mathrm{[Hz]}}\)、1秒間に回転する角度(角速度)は\({\omega}=2π×10{\mathrm{[rad/s]}}\)となります。

なお、(6)式を用いれば、『\(e=E_{M}{\sin}{\omega}t\)』は以下のように書き換えることもできます。

\begin{eqnarray}
e&=&E_{M}{\sin}{\omega}t\\
&=&E_{M}{\sin}2{\pi}ft\\
&=&E_{M}{\sin}2{\pi}\frac{t}{T}
\end{eqnarray}

交流発電機の誘導起電力の向き

誘導起電力の向きはレンツの法則によって求めることができます。

レンツの法則とは、「電磁誘導によって生じる誘導起電力の向き」を表した法則です。誘導起電力の向きは「元の磁束の変化を妨げる方向」となります。

レンツの法則について詳しくは以下の記事に説明していますので、参考にしてください。

: 【レンツの法則とは】起電力の向きについてわかりやすく解説！
続きを見る

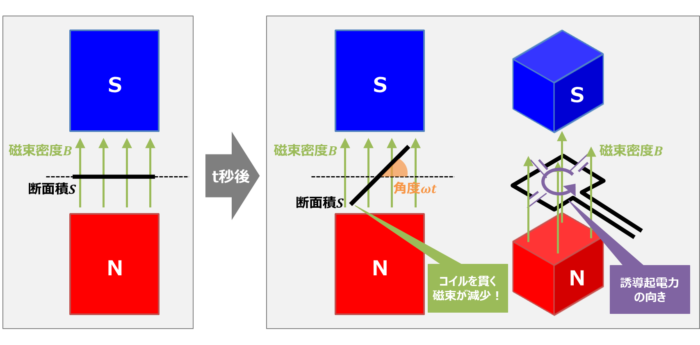
例えば、一様な磁束密度\(B{\mathrm{[T]}}\)とコイルの向きが垂直の状態から、コイルが回転した時を考えてみましょう。

\(t\)秒後、コイルが回転したことによって、コイル面と磁束密度\(B{\mathrm{[T]}}\)のなす角は\({\omega}t{\mathrm{[rad]}}\)となります。その結果、コイルを貫く磁束が減少しています。

すると、レンツの法則によって、磁束の変化を妨げる方向(下から上)に磁束を発生させるように、反時計回りの向きに誘導起電力が生じます。

例題

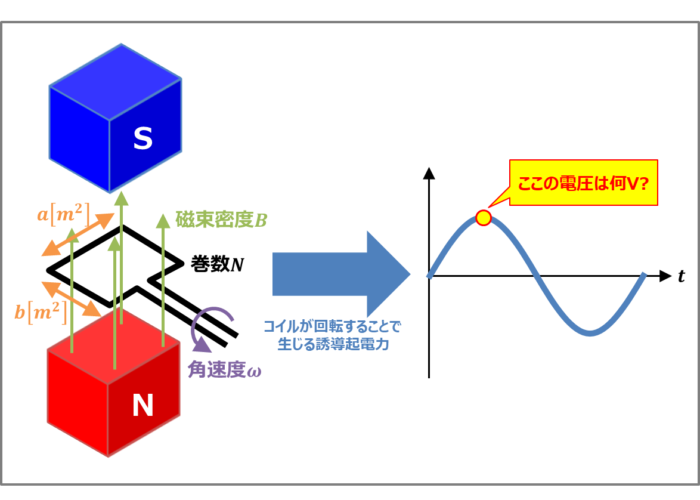
各辺の長さ\(a{\mathrm{[m]}}\)、\(b{\mathrm{[m]}}\)で巻数\(N\)の長方形コイルが一様な磁束密度\(B{\mathrm{[T]}}\)の中で、角速度\({\omega}{\mathrm{[rad/s]}}\)で回転している時、コイルに誘導される起電力の最大値は何ボルトか？