【磁界の強さのまとめ】『直流導体』・『円形コイル』・『無限長ソレノイド』・『環状ソレノイド』

この記事では磁界の強さについて

様々な導体の磁界の強さのまとめ
直流導体による磁界の強さ
円形コイルによる磁界の強さ
無限長ソレノイドコイルによる磁界の強さ
環状ソレノイドコイルによる磁界の強さ

などを図を用いて分かりやすく説明しています。

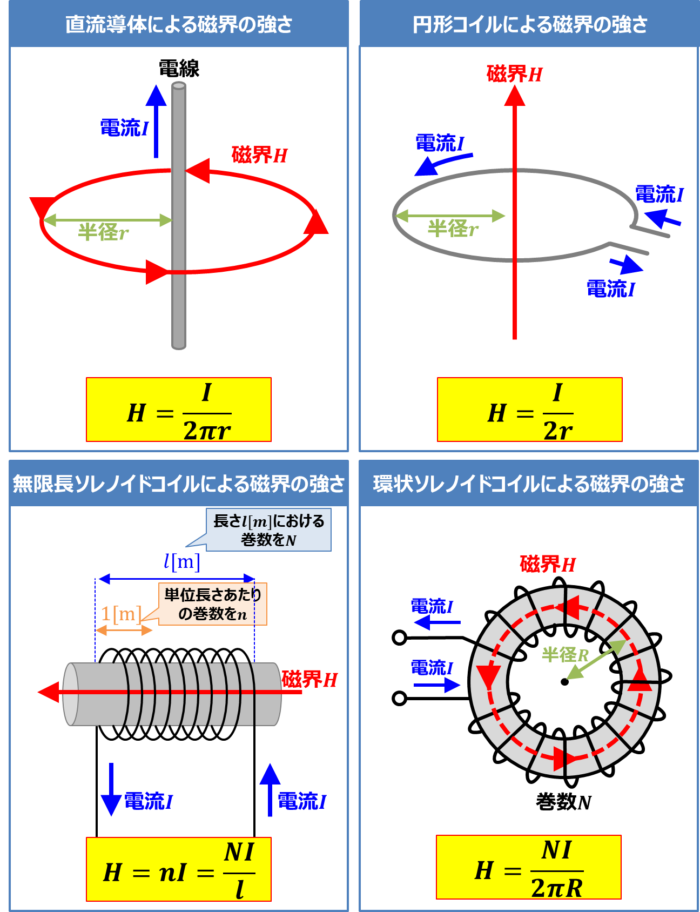
様々な導体の磁界の強さまとめ

導体に電流が流れると磁界が発生します。

この時、磁界の向きと磁界の強さは以下の法則によって決まります。

磁界の向きと磁界の強さを決める法則

磁界の向き

『アンペアの右ネジの法則(右手の法則とも呼ばれる)』によって決まります。

磁界の強さ

『アンペアの周回積分の法則(アンペアの周回路の法則)』や『ビオ・サバールの法則』によって決まります。

この記事では、各導体(『直流導体』・『円形コイル』・『無限長ソレノイド』・『環状ソレノイド』)に電流\(I{\mathrm{[A]}}\)が流れた時の、磁界の向きと磁界の強さをまとめています。

なお、『アンペアの周回積分の法則』と『ビオ・サバールの法則』を用いて各導体の磁界の強さを求める方法については、以下の記事で説明していますので、参考にしてください。

: 【アンペアの周回積分の法則とは】図を用いてわかりやすく説明！
続きを見る

: 【ビオ・サバールの法則とは】『直流電流』や『円電流』の磁界の強さの導出など！
続きを見る

直流導体による磁界の強さ

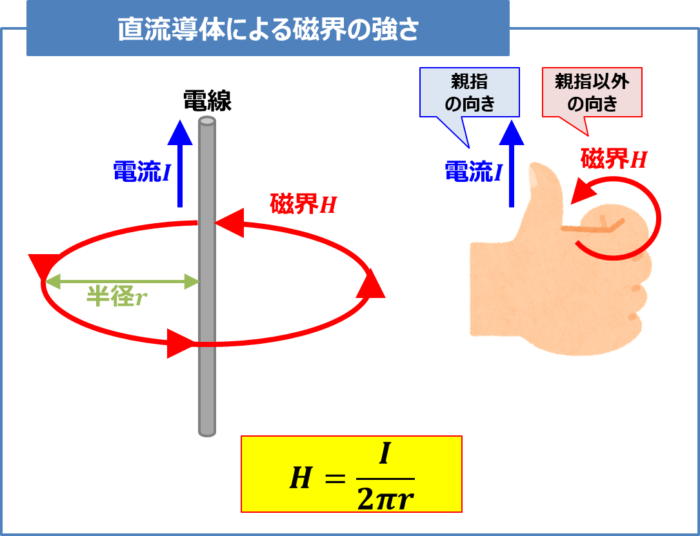
1本の直流電線に電流\(I{\mathrm{[A]}}\)流れると、磁界は『アンペアの右ネジの法則(右手の法則とも呼ばれる)』より円形状の磁界ができます。

この時、電線から半径\(r{\mathrm{[m]}}\)離れた磁界の強さ\(H{\mathrm{[A/m]}}\)は次式で求めることができます。

\begin{eqnarray}
H=\frac{I}{2{\pi}r}{\mathrm{[A/m]}}\tag{1}
\end{eqnarray}

円形コイルによる磁界の強さ

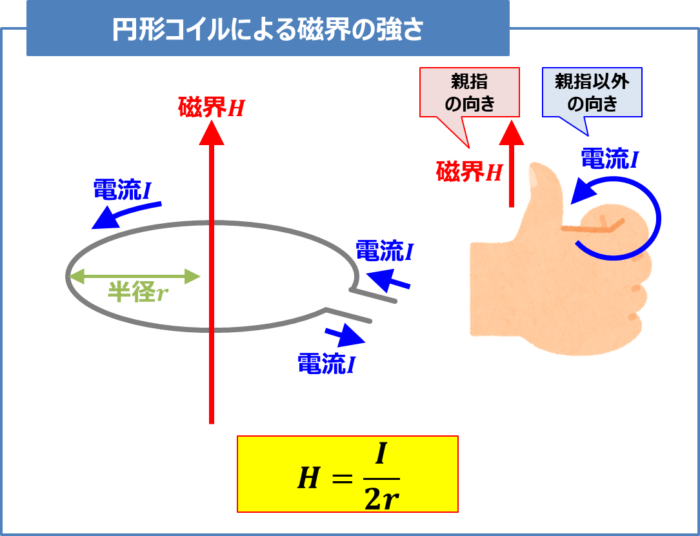
半径\(r{\mathrm{[m]}}\)の\(1\)回巻き円形コイルに電流\(I{\mathrm{[A]}}\)流れると、磁界は『アンペアの右ネジの法則(右手の法則とも呼ばれる)』より直線状の磁界ができます。

この時、円形コイル中心の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式で求めることができます。

\begin{eqnarray}
H=\frac{I}{2r}{\mathrm{[A/m]}}\tag{2}
\end{eqnarray}

無限長ソレノイドコイルによる磁界の強さ

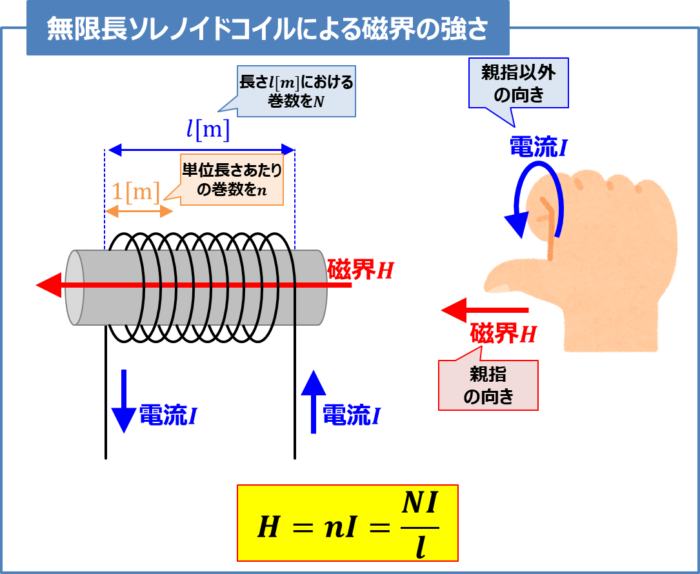
単位長さあたり(\(1{\mathrm{[m]}}\)あたり)の巻数が\(n\)の無限長ソレノイドコイルに電流\(I{\mathrm{[A]}}\)が流れると、磁界は『アンペアの右ネジの法則(右手の法則とも呼ばれる)』より直線状の磁界ができます。

この時、ソレノイド内部の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式となります。

\begin{eqnarray}
H=nI{\mathrm{[A/m]}}\tag{3}
\end{eqnarray}

また、長さ(\(l{\mathrm{[m]}}\)あたり)における巻数を\(N\)とすると、『長さ\(l{\mathrm{[m]}}\)における巻数\(N\)』と『長さ\(1{\mathrm{[m]}}\)あたりの巻数\(n\)』は次式の関係があります。

\begin{eqnarray}
n=\frac{N}{l}\tag{4}
\end{eqnarray}

(4)式を(3)式に代入すると、次式となります。

\begin{eqnarray}
H=\frac{NI}{l}{\mathrm{[A/m]}}\tag{5}
\end{eqnarray}

環状ソレノイドコイルによる磁界の強さ

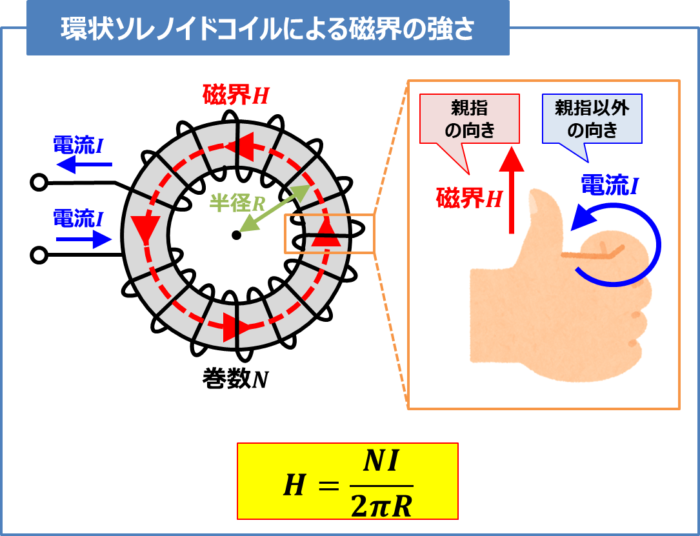
巻数\(N\)、平均半径\(R{\mathrm{[m]}}\)(平均磁路長\(l=2{\pi}R{\mathrm{[m]}}\))の環状ソレノイドに電流\(I{\mathrm{[A]}}\)が流れると、磁界は『アンペアの右ネジの法則(右手の法則とも呼ばれる)』よりソレノイドコイルの内部に磁界ができます。

この時、ソレノイド内部の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式となります。

\begin{eqnarray}
H=\frac{NI}{2{\pi}R}{\mathrm{[A/m]}}\tag{6}
\end{eqnarray}