【基本事項1】物体を等価回路に変換する
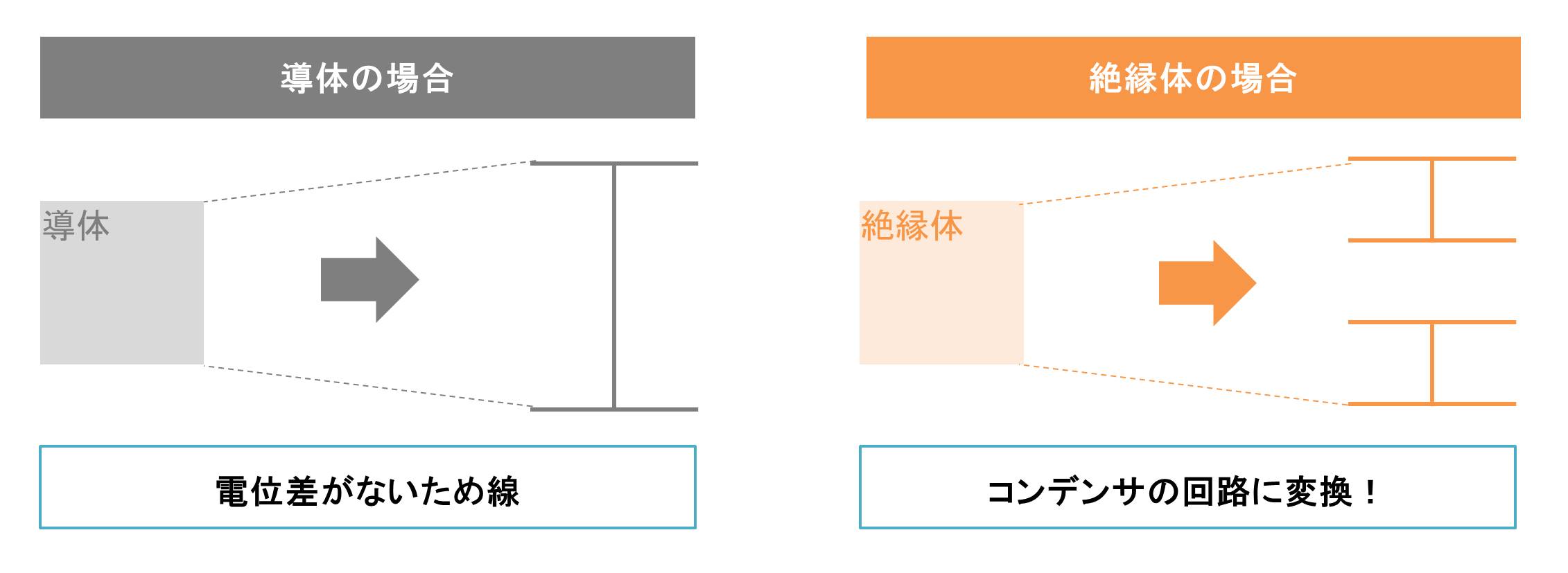
物体の表面電位を計算するうえで、導体と絶縁体を等価回路に直す必要があります。これが非常に重要です。導体は内部で電位差が生じないため、ただの線になりますが、絶縁体は電場が内部に入り込むことが可能なため、電位差が生じます。その結果、絶縁体は等価回路がコンデンサとなります。
また、物体(導体や絶縁体)は地面(GND)と対地静電容量というコンデンサを構成しています。地面に対するコンデンサというイメージでよいですよ。
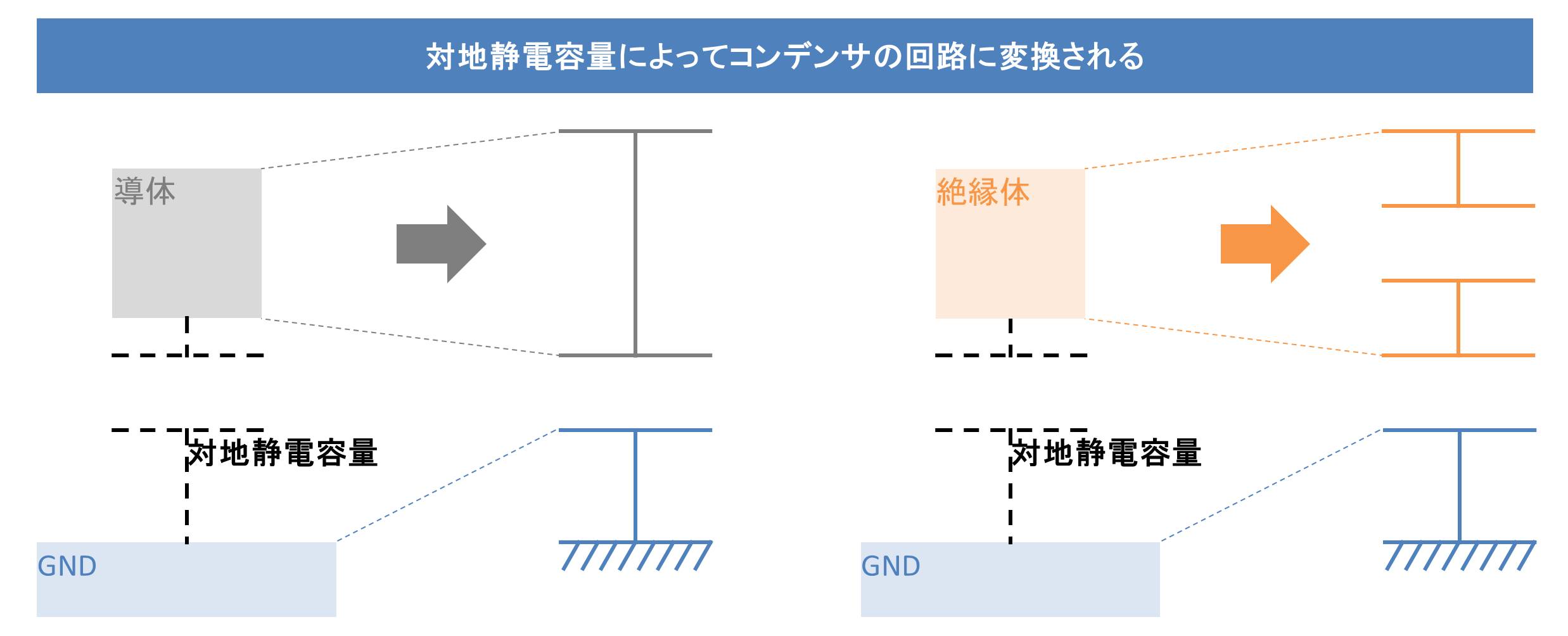
これらの組み合わせで等価回路が決まります。このように等価回路に直すことで理解しにくい表面電位を中学や高校で習うコンデンサの回路に変換できます。
【基本事項2】導体と絶縁体の電荷状態について
■導体の場合
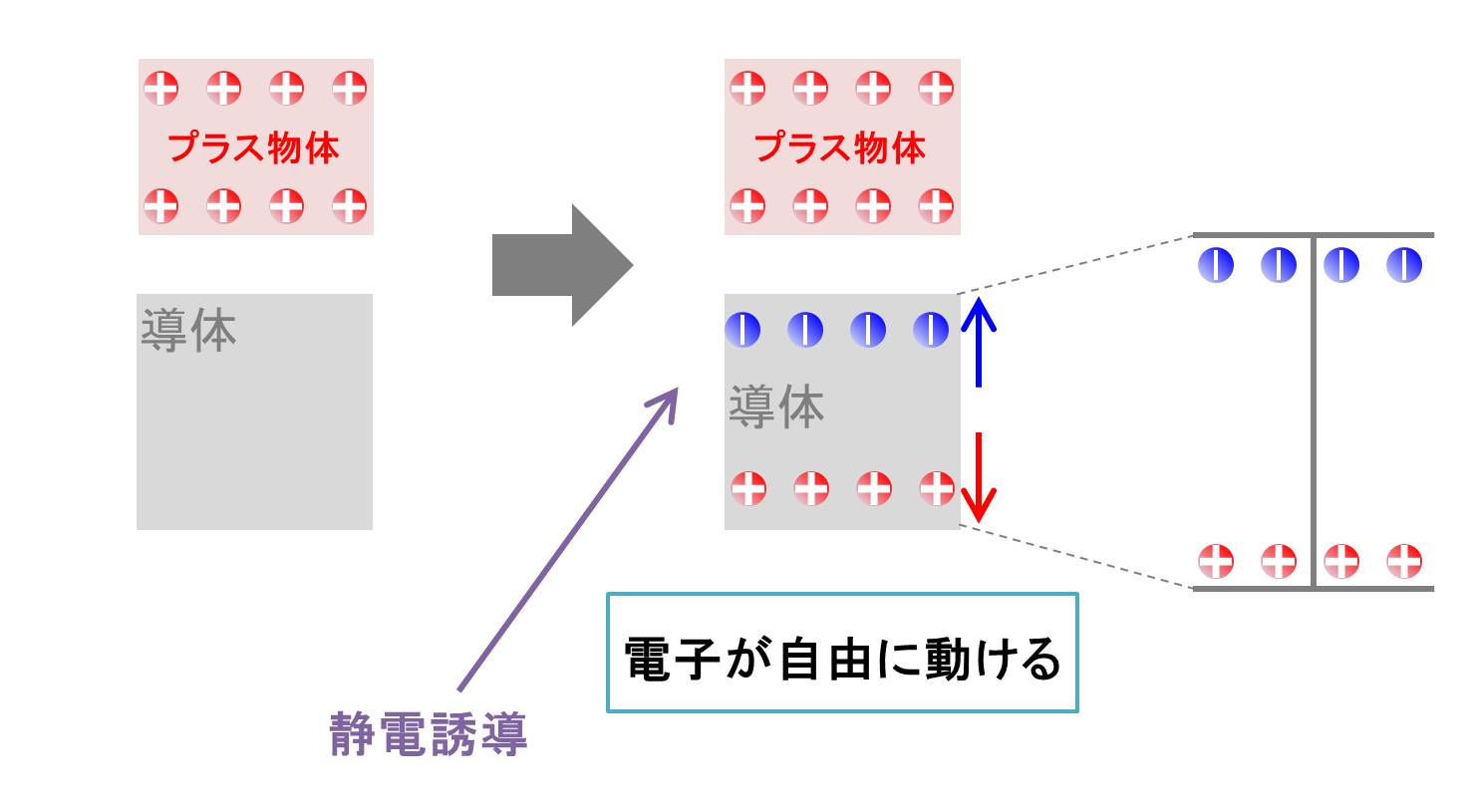
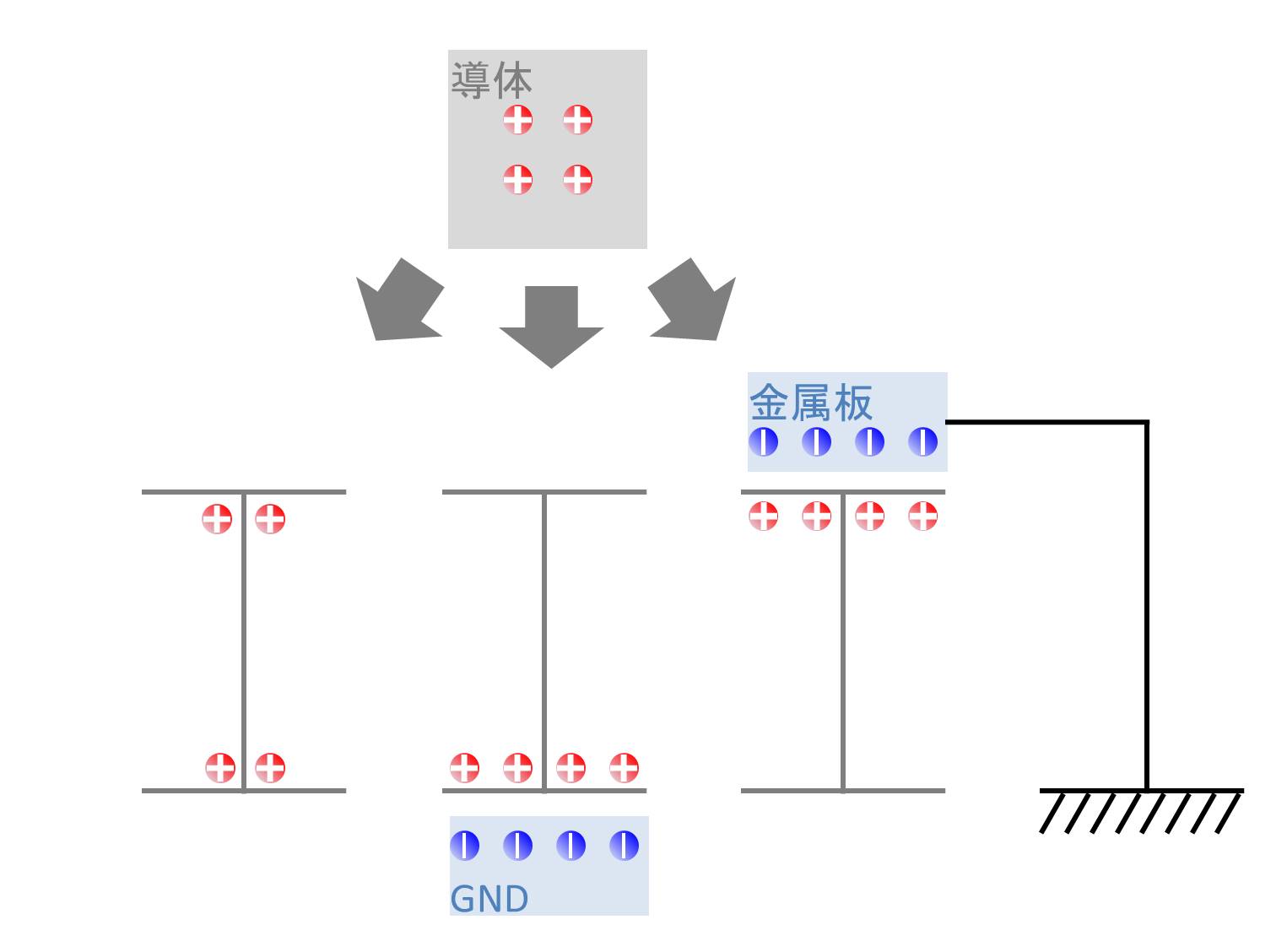
導体は内部で電子が自由に動くことが可能です。そのため、プラスに帯電した物体やマイナスに帯電した物体が導体に近づいたとき、導体内部の電荷の状態はこのようになります(静電誘導といいます)。
電荷がどのように分布するかは外部の状態によって変化します。例えば、プラスに帯電している導体があり、外部に何も物体がない状態では、プラス電荷は均等に分布しますが、マイナス電荷が導体下面などに存在すると、プラス電荷はマイナス電荷に引き寄せられ、導体下面の方に集中します。
■絶縁体の場合
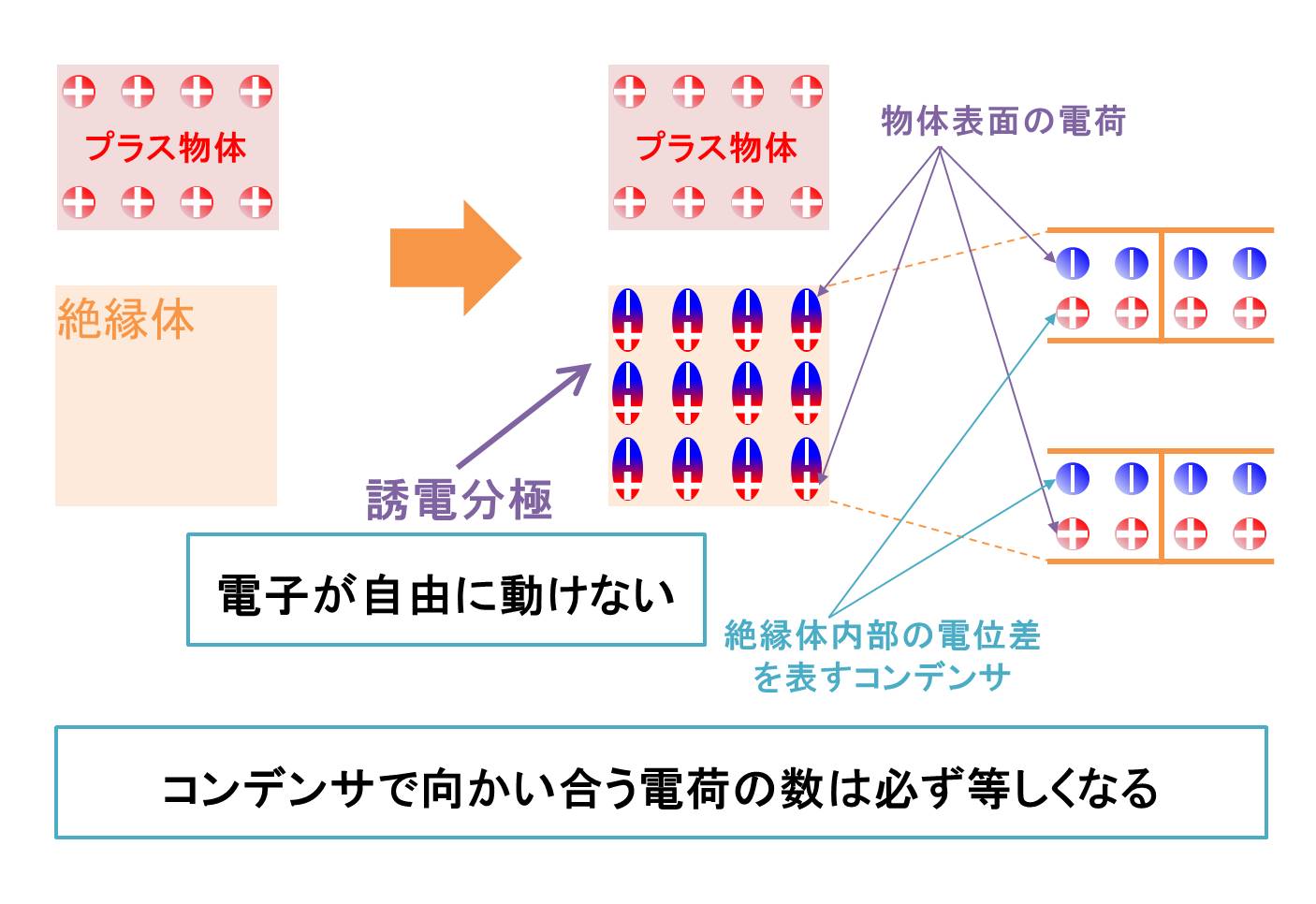
一方、絶縁体は電子が自由に動くことができません。そのため、プラスに帯電した物体やマイナスに帯電した物体が近づいたとき、電荷の状態はこのようになります(誘電分極といいます)。絶縁体は外部の電場をすべて打ち消すことができません。そのため、絶縁体内部には電場があり、電位差が生じます。この電位差をコンデンサで表します。なお、コンデンサで向かい合う電荷の数は必ず等しいです。これは今後かなり重要となります。決して電位差があるから電荷の数を変えることや、絶縁体上面と下面で存在する電荷の数を変えないようにしてください。
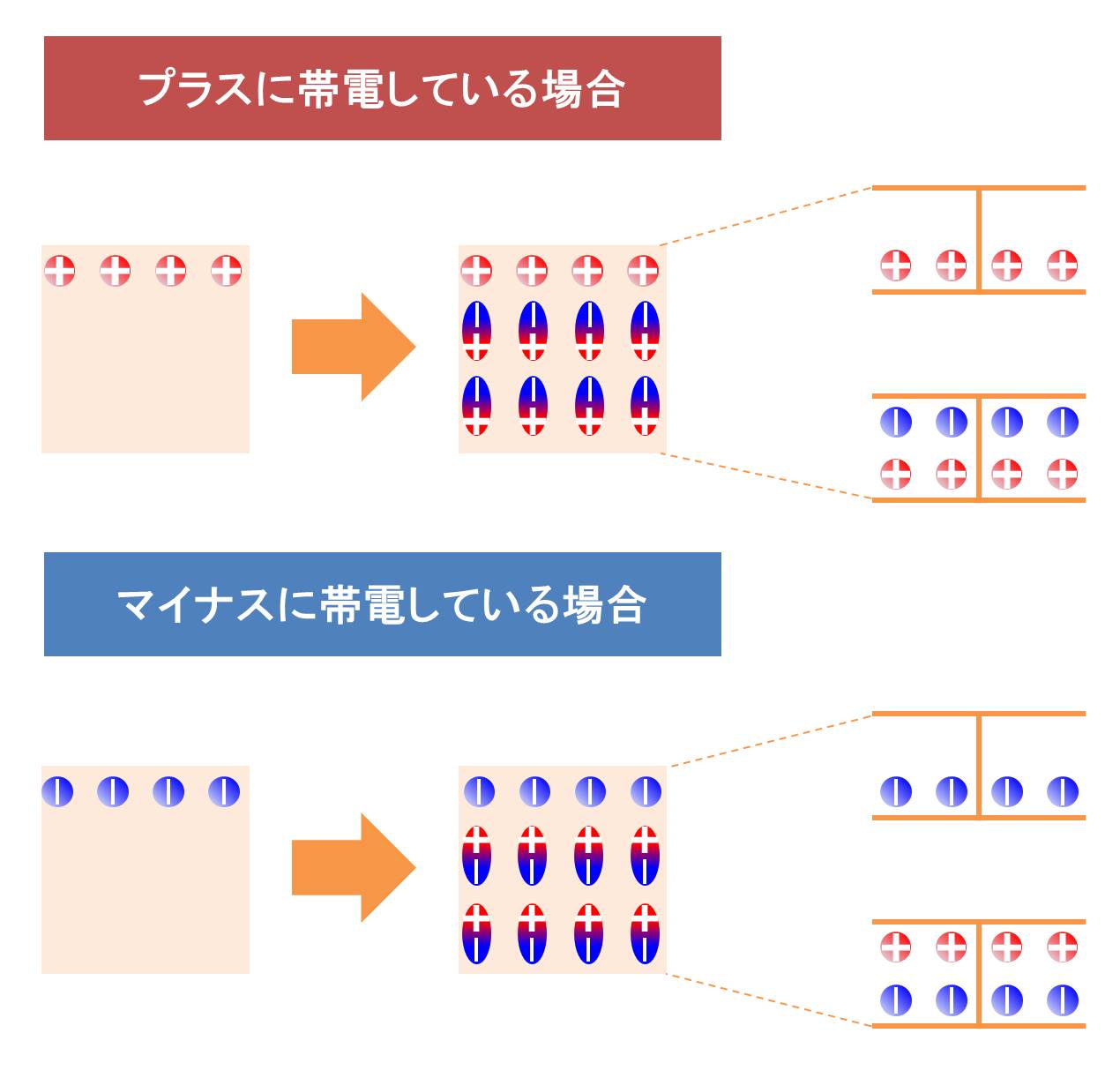
絶縁体がプラスやマイナスに帯電しているときはこのようになります。全体としてプラスに帯電していれば、合計の電荷がプラス、マイナスに帯電していれば電荷の合計がマイナスになっています。なお、絶縁体の上面と下面で電位差があるため、電位差を表すコンデンサはもちろんあります。
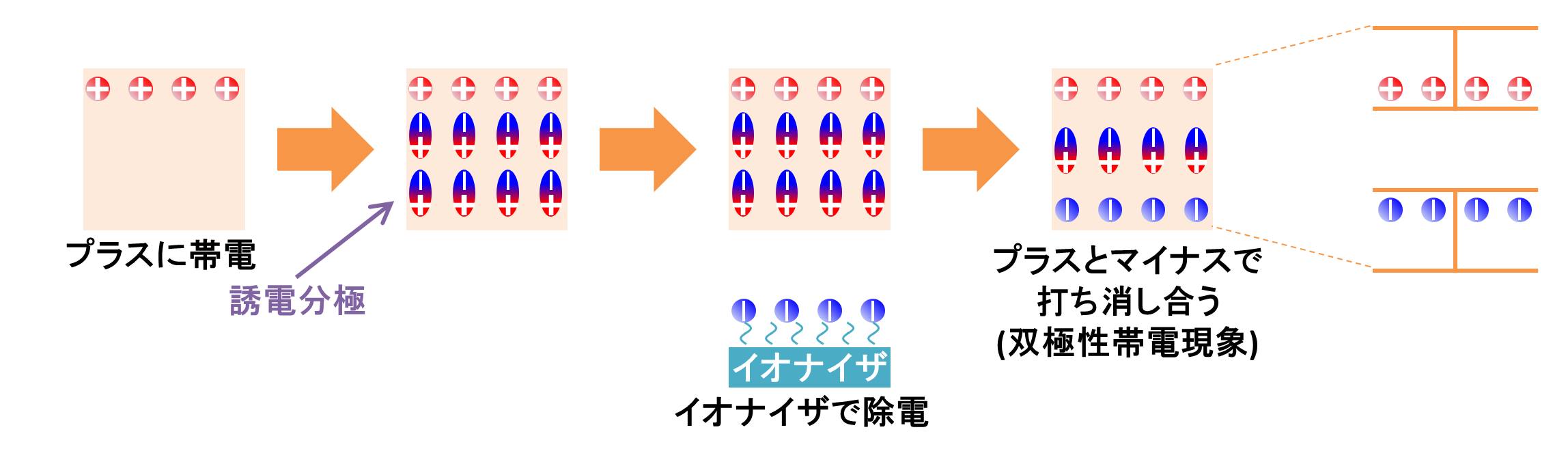
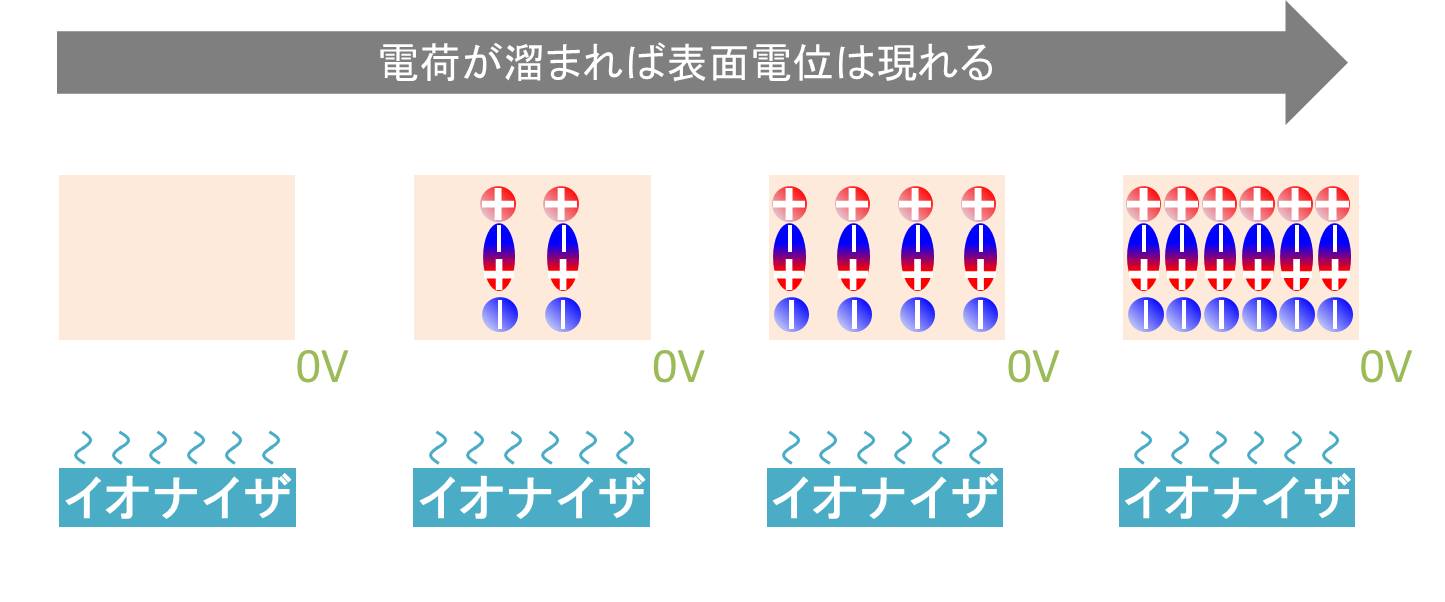
ここで帯電していない方を除電します(イオナイザを使用。コンデンサでいうと接地みたいな感じ)。例えば、絶縁体の上面が帯電しているとき、分極によって下面にはプラスが見えます。このプラスを除電するため、下面はマイナス電荷が付着します。その結果、絶縁体はコンデンサを構成してしまいます。これは絶縁体内部の電子が移動できないことによって生じる現象です。つまり、絶縁体のある部分はプラスに帯電し、ある部分はマイナスに帯電していますが、物体の総電荷量がゼロとなります。(専門用語でいうと双極性帯電現象といいます)。
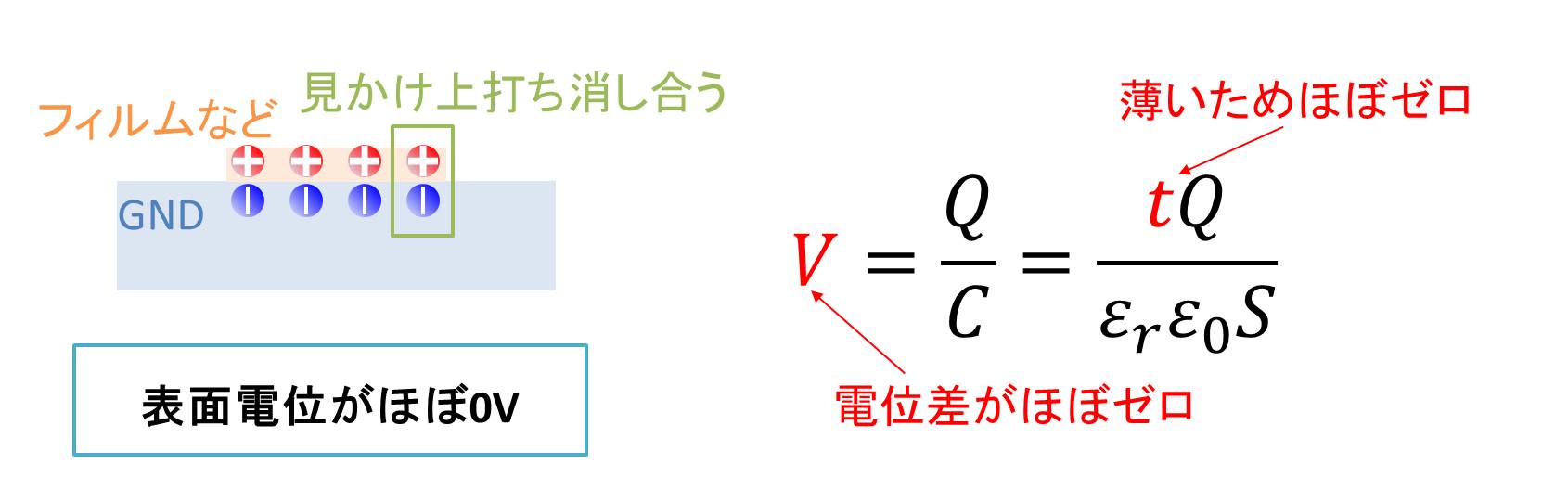
絶縁体がフィルム等薄いものだと、プラスとマイナスが打ち消し合っているようにみえ、帯電しているにも関わらず、見かけ上0Vになってしまいます。これは、コンデンサの式の厚さtが小さいためです。
孤立した帯電導体の場合
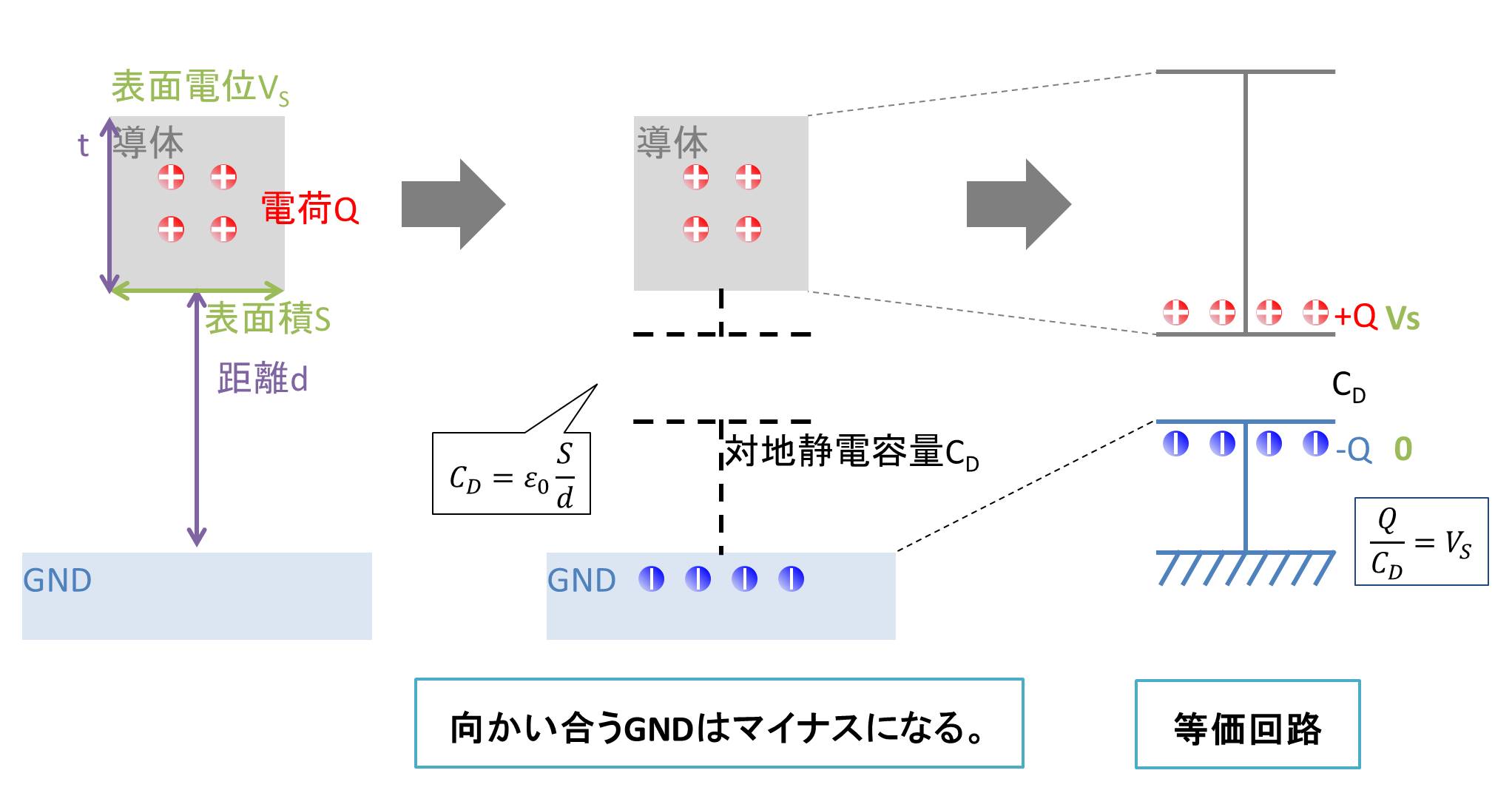
ではここから表面電位がどのように決まるのかを様々な例で解説します。まずは、距離d離れた場所に表面積がS、厚さtの孤立した導体がある場合です。導体の帯電電荷は+Qであり、導体上面の表面電位がVSと仮定します。この時、導体と向かい合うGNDは導体のプラス電荷に引き付けられ、マイナスになり、導体下面とGNDの間に対地静電容量CDができます。なお、導体内部の電位差はゼロなので、導体下面の電位もVSとなります。
まず、コンデンサの式(Q=CV)から、
$$ V_S= \frac{Q}{C_D}$$
ここで、対地静電容量CDは
$$ C_D = {\varepsilon_0} \frac{S}{d}$$
ここで、ε 0は真空の誘電率です。
そのため、導体の表面電位VSは
$$ V_S= \frac{Q}{C_D}= \frac{dQ}{{\varepsilon_0}S}$$
となります。
孤立した帯電導体を持ち上げた場合
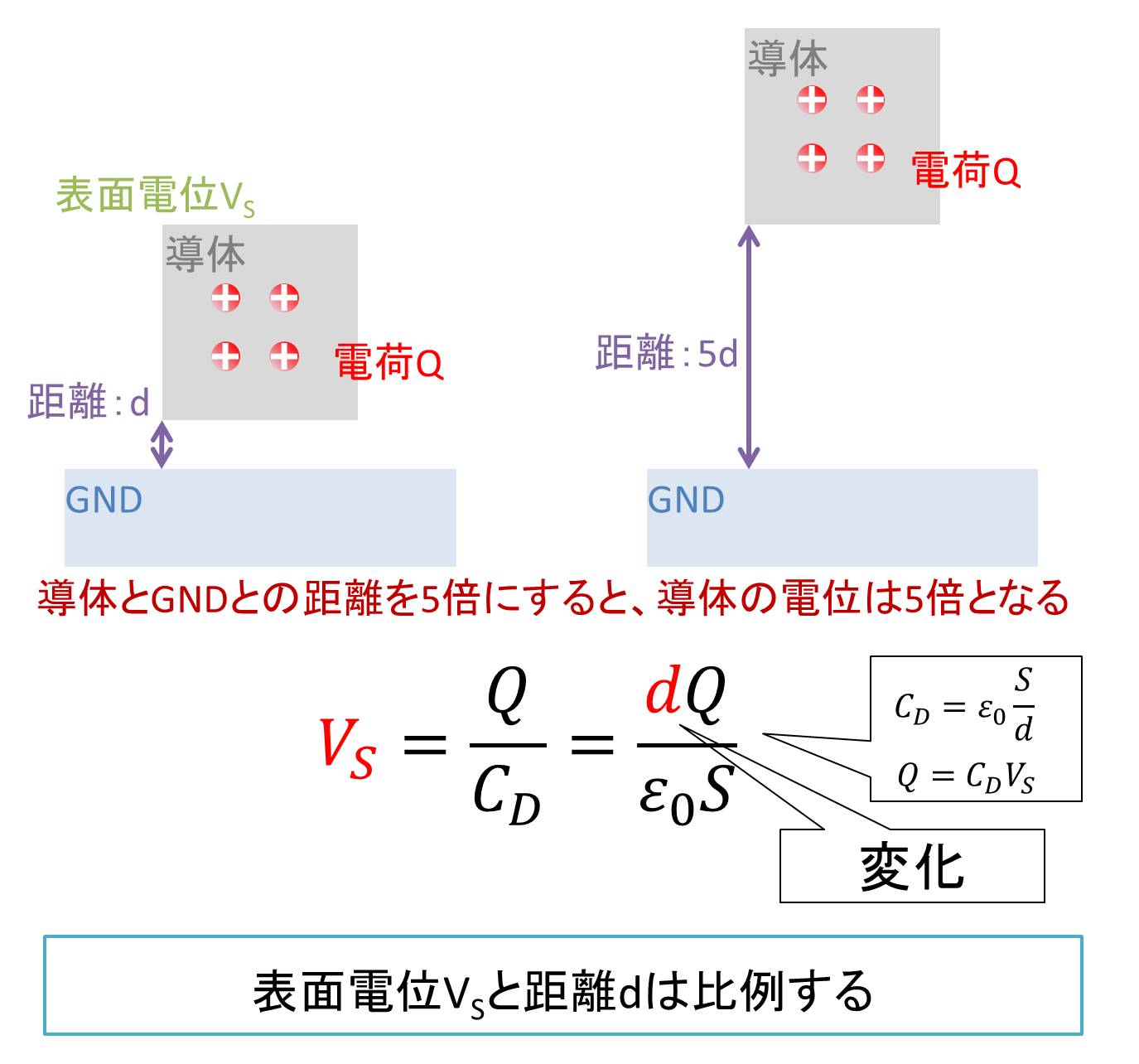
では、孤立した帯電導体を持ち上げたらどのようになるでしょうか。今回は、距離d離れた場所に表面積がSの孤立した導体がある状態(この時の帯電電荷がQであり、導体上面の表面電位をVSとする)から、距離5dと5倍の距離に持ち上げた時に表面電位VSがどうなるか計算してみます。
帯電している導体を持ち上げたときに電荷Qがリークして逃げないと仮定すると、表面電位VSと距離dは比例します。そのため。距離を5倍にすると、表面電位は5倍となります。
孤立した帯電絶縁体の場合
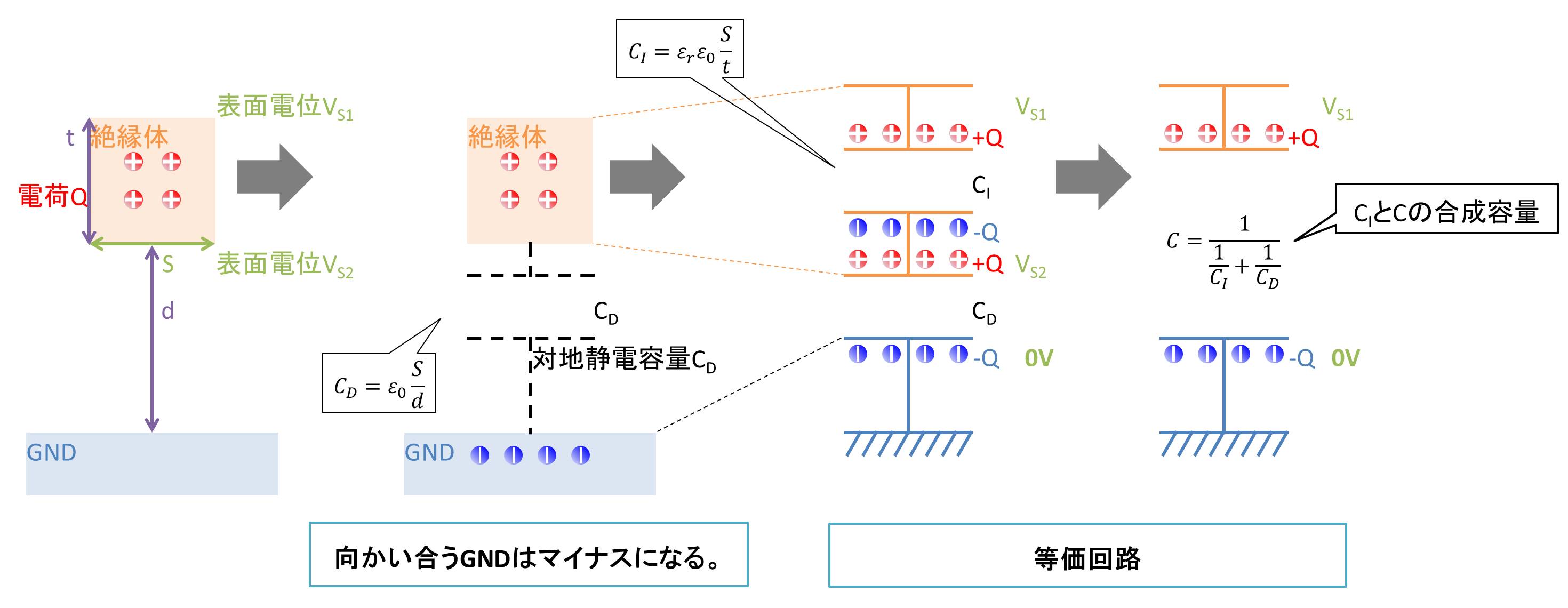
今度は導体ではなく、絶縁体の場合を考えています。距離d離れた場所に表面積がS、厚さがtの孤立した絶縁体がある場合です。絶縁体上面の帯電電荷が+Qであり、絶縁体上面の表面電位がVS1と仮定します。この時、絶縁体と向かい合うGNDはマイナスとなり、絶縁体下面とGNDの間に対地静電容量CDができます。なお、絶縁体は電位差が生じます。そのため、絶縁体下面の表面電位は絶縁体上面の表面電位VS1と同じになりません。今回は絶縁体下面の表面電位をVS2と仮定します。
絶縁体を絶縁板を挟んだ平行平板コンデンサ(容量CI)と仮定すると、
$$ C_I = {\varepsilon_0}{\varepsilon_r} \frac{S}{d}$$
対地静電容量CDは
$$ C_D = {\varepsilon_0} \frac{S}{d}$$
ここで、ε 0は真空の誘電率、ε rは絶縁体の比誘電率です。
ゆえに絶縁体上面から見た対地静電容量CはCIとCDの直列接続となるため
$$ C_D = \frac{1}{\frac{1}{ C_I }+\frac{1}{ C_D}}$$
となるため、絶縁体上面の表面電位VS1は
$$ V_{S1} = \frac{Q}{C} = \frac{Q}{C_I}(1+\frac{ C_I }{C_D})$$
となります。
つまり、絶縁体を持ち上げると、CI/ CDが増加します。増加は持ち上げた距離dに比例します。例えば、薄いフィルムが地面にあるときは、CIが非常に大きいため、電位はほぼゼロですが、このフィルムを数mmでも持ち上げると、CDが現れ、急激に表面電位が増加します。また、距離が1mmから2mmになると倍です。また、1mから2mでも倍です。つまり、高い場所にあるものは距離を変えても変化率が小さくなります。
孤立した帯電絶縁体を持ち上げた場合
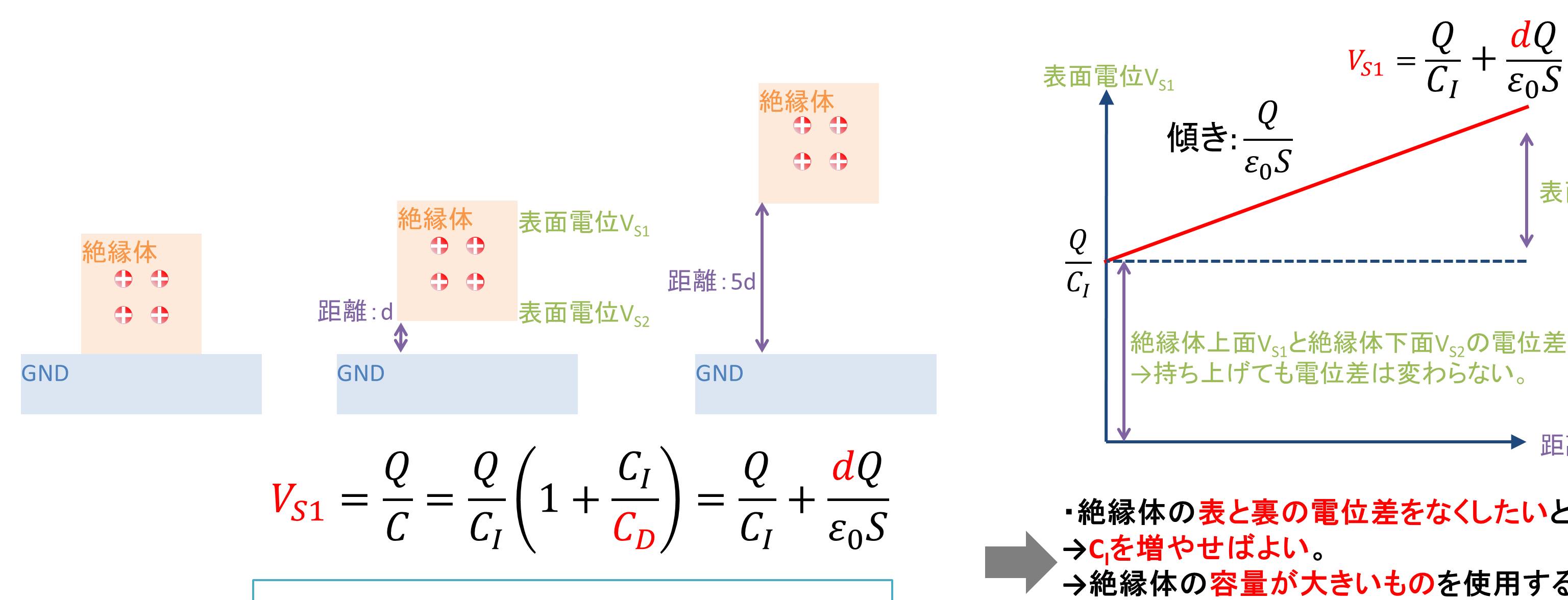
では、孤立した帯電絶縁体を持ち上げたらどのようになるでしょうか。導体の場合は比例しましたが、絶縁体の場合は比例しません。帯電している絶縁体を持ち上げたときに電荷Qがリークして逃げないと仮定すると、絶縁体の容量CIは一定なので、変数は距離dのみになります。式を図で表すと線形増加となることがわかります。この図で分かることは2つあります。
①最初の表面電位Q/CIが大きい場合、すなわち誘電率が低い絶縁体を使用した場合、距離による変化率は小さくなります(例:1000Vから1500Vのような感じ)。
②最初の表面電位Q/CIが小さい場合、すなわち誘電率が低い絶縁体や薄いフィルム等を使用した場合、数mmでも持ち上げると、急激に表面電位があがります(例:0Vから500Vのような感じ)。
③絶縁体上面と絶縁体下面の電位差(VS1- VS2)は絶縁体を持ち上げても変わりません。これより絶縁体の表と裏の電位差をなくしたいときは誘電率の高いものを使用すればよいことがわかります。
絶縁体の厚さが異なる場合
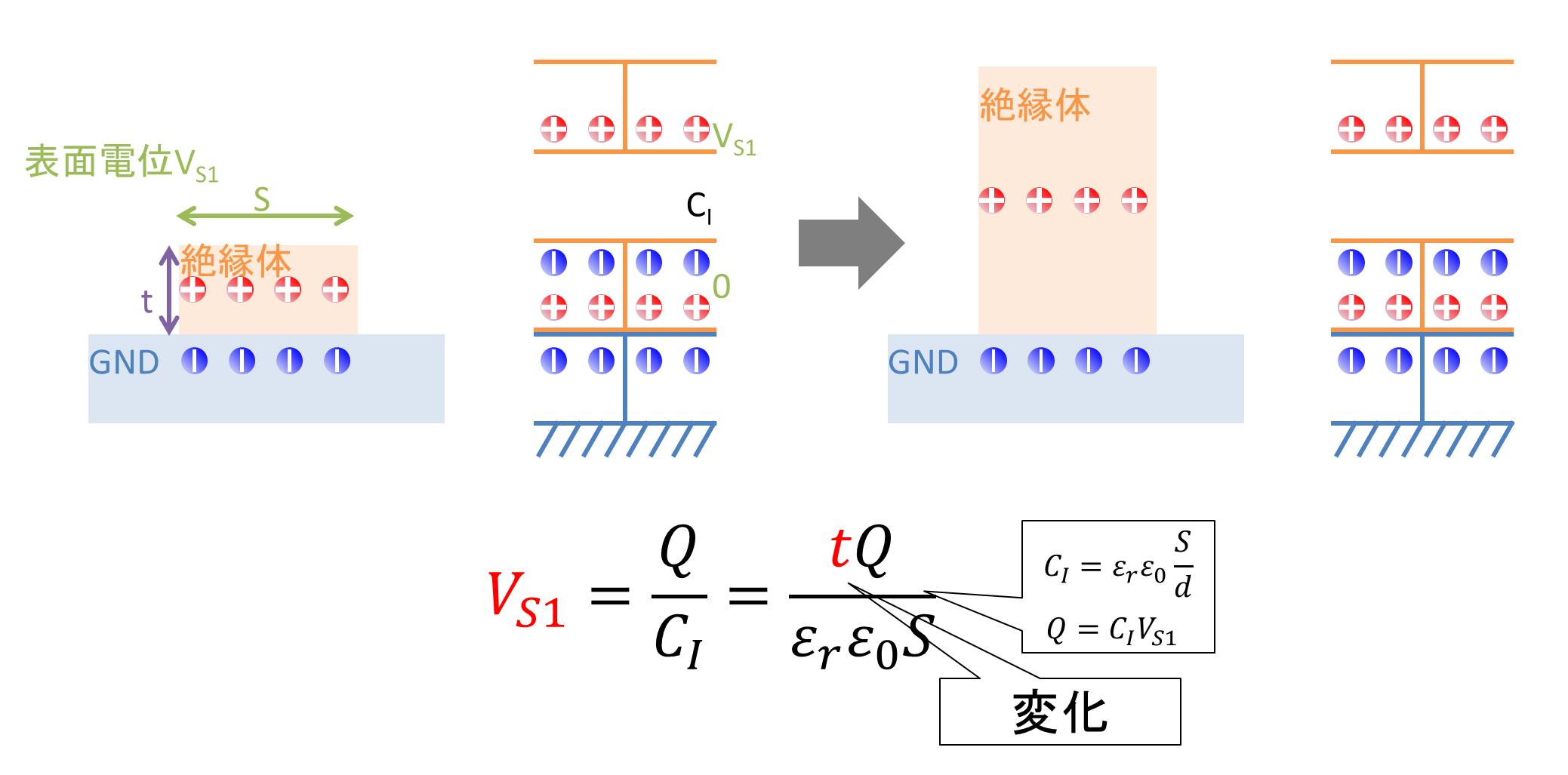
絶縁体が厚い場合は地面においても表面電位が現れますが、絶縁体が薄いフィルム等は地面に置くと表面電位VSが見えなくなります。その理由を解説します。
絶縁体を絶縁板を挟んだ平行平板コンデンサ(容量CI)と仮定すると、
$$ C_I = {\varepsilon_0}{\varepsilon_r} \frac{S}{d}$$
コンデンサの式(Q=CV)から、絶縁体の表面電位VSは
$$ V_S= \frac{Q}{C_I}= \frac{dQ}{{\varepsilon_0}{\varepsilon_r}S}$$
となります。これより厚い絶縁体の方が表面電位は大きくなることがわかります。
例えば、フィルム等はとても薄いため、容量CIが大きくなります。すなわち、表面電位VSは0Vに近い値となります。
余談ですが、これは先ほど説明した双極性帯電現象にとってはとても重要な現象です。フィルムなど薄い物体は帯電していない方を間違えて除電しても、表面電位は0Vに近い値となります。(ただし、かなり帯電させ電荷Qを大きくすると、薄くても表面電位は上がります)。

帯電導体→導体→GNDの場合
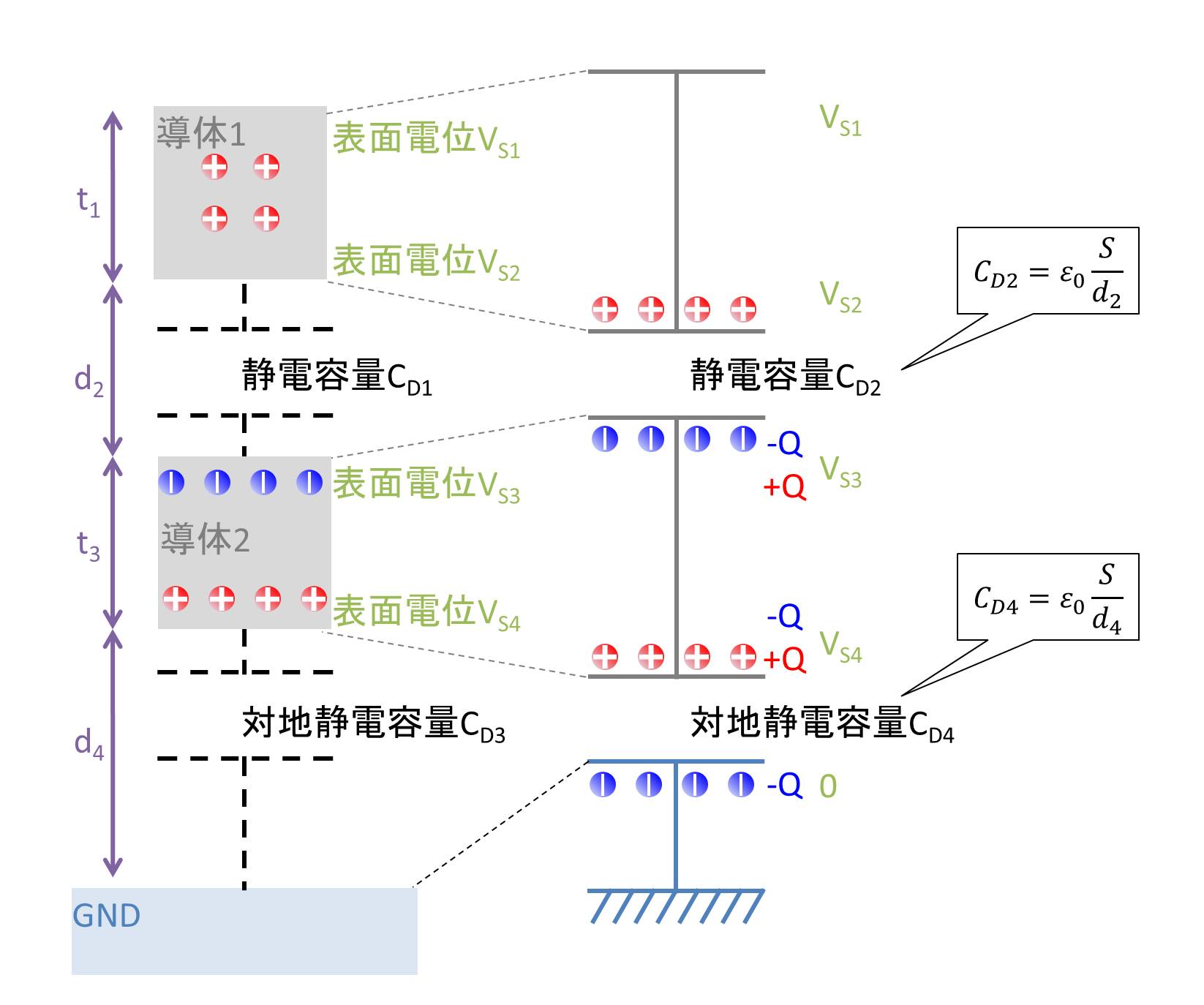
次は、物体が2つあるときについてです。このような図の場合を想定します。
導体1の厚さをt1、導体2の厚さをt3、導体1と導体2の距離をd2、導体2とGNDとの距離をd4とします。この時、導体1の表面電位は等しいため、VS1=VS2となります。また導体2の表面電位も等しいため、VS3=VS4となります。
導体2は帯電導体1と同じ極性の電位を持ちます。導体2の表面電位VS3, VS4は、帯電導体1と導体2の静電容量CD2と導体2の対地静電容量CD4で帯電導体1の表面電位VS1, VS2を分圧した値となります。すなわち
$$ V_{S3} = V_{S4} = \frac{\frac{1}{ C_{D4}}}{\frac{1}{ C_{D2}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{d_4}{{d_2}+{d_4}} V_{S1}$$
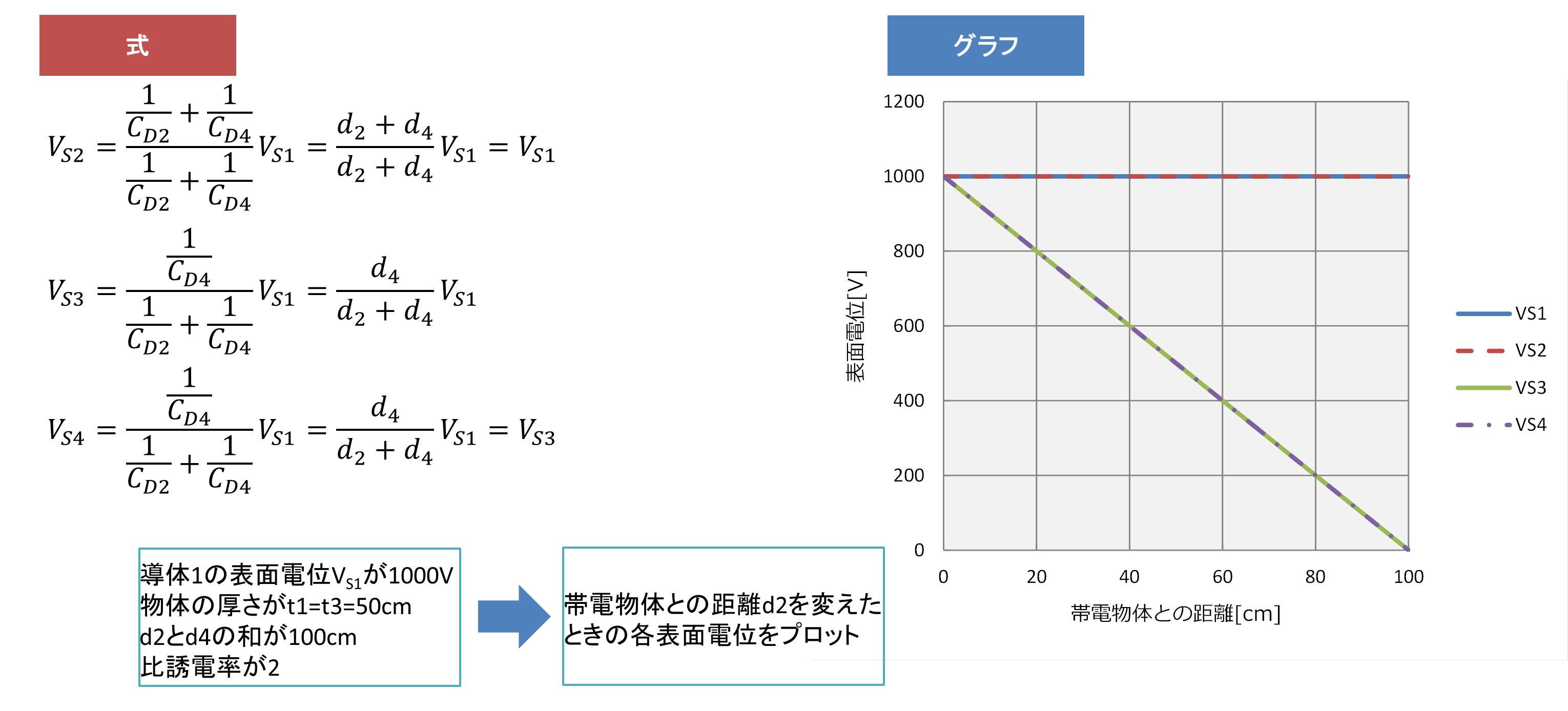
となります。例として導体1の表面電位VS1, VS2が1000V、物体の厚さがt1= t3=50cm、d2とd4の距離の和が100cmの時に導体2を上下に移動させた時の各表面電位をグラフに示します。このように、帯電物体との距離が0cmの時、導体2の表面電位VS3, VS4が1000Vであり、そこから線形的に減少していくことがわかります。100cmの時、すなわちGNDに接続されたときはもちろん表面電位VS3, VS4は50cmとなります。
帯電導体→絶縁体→GNDの場合
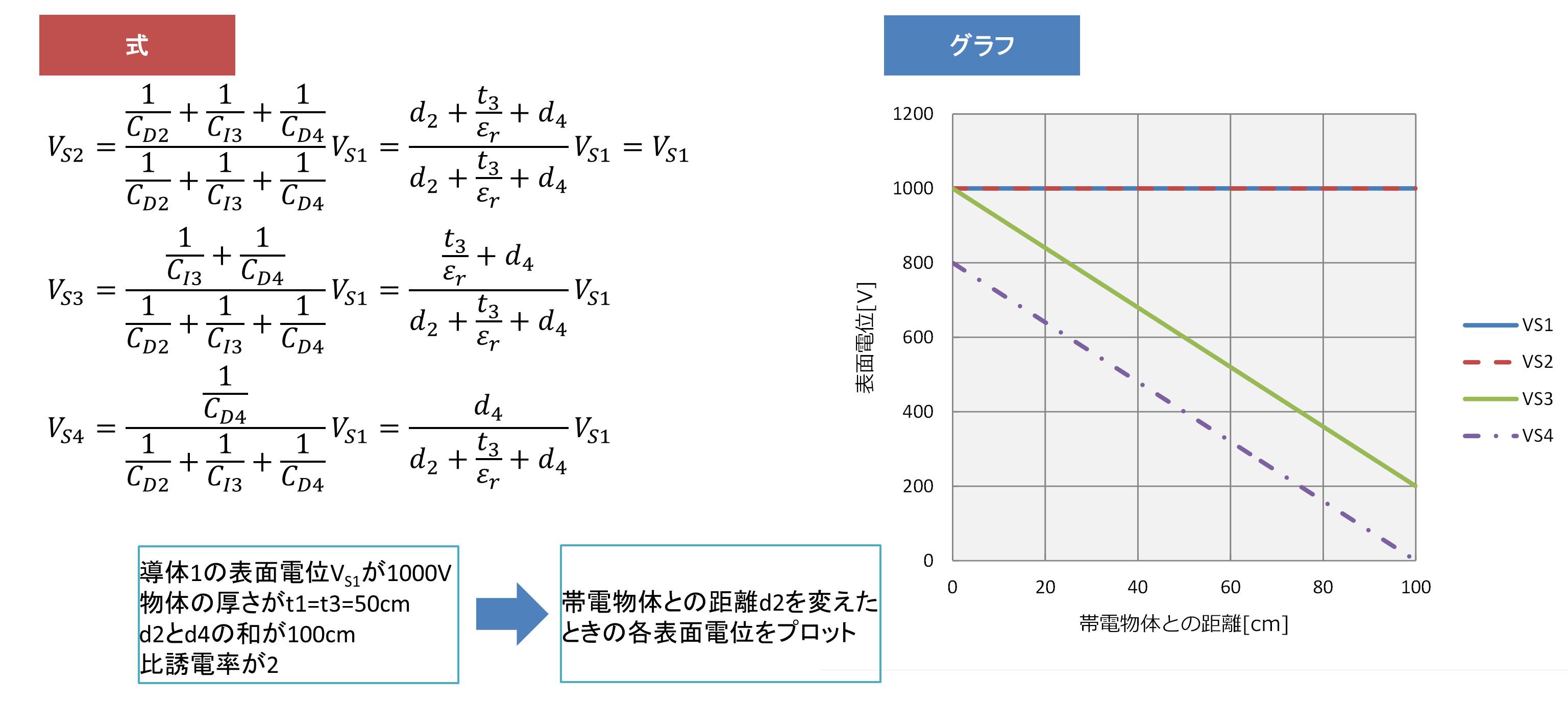
中心の物体が絶縁体の場合です。これはこのような図になります。
導体1の厚さをt1、絶縁体2の厚さをt3、導体1と絶縁体2の距離をd2、絶縁体2とGNDとの距離をd4とします。この時、導体1の表面電位は等しいため、VS1=VS2となります。
絶縁体2は帯電導体1と同じ極性の電位を持ちます。絶縁体2の表面電位VS3は、帯電導体1と絶縁体2の静電容量CD2と絶縁体2内部の静電容量CI3、絶縁体2の対地静電容量CD4の分圧となるため、
$$ V_{S3} = \frac{\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}}{\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{\frac{t_3}{\varepsilon_r}}+{d_4}}{{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}} V_{S1}$$
同様に、絶縁体2の表面電位VS4は
$$ V_{S4} = \frac{\frac{1}{ C_{D4}}}{\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{d_4}{{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}} V_{S1}$$
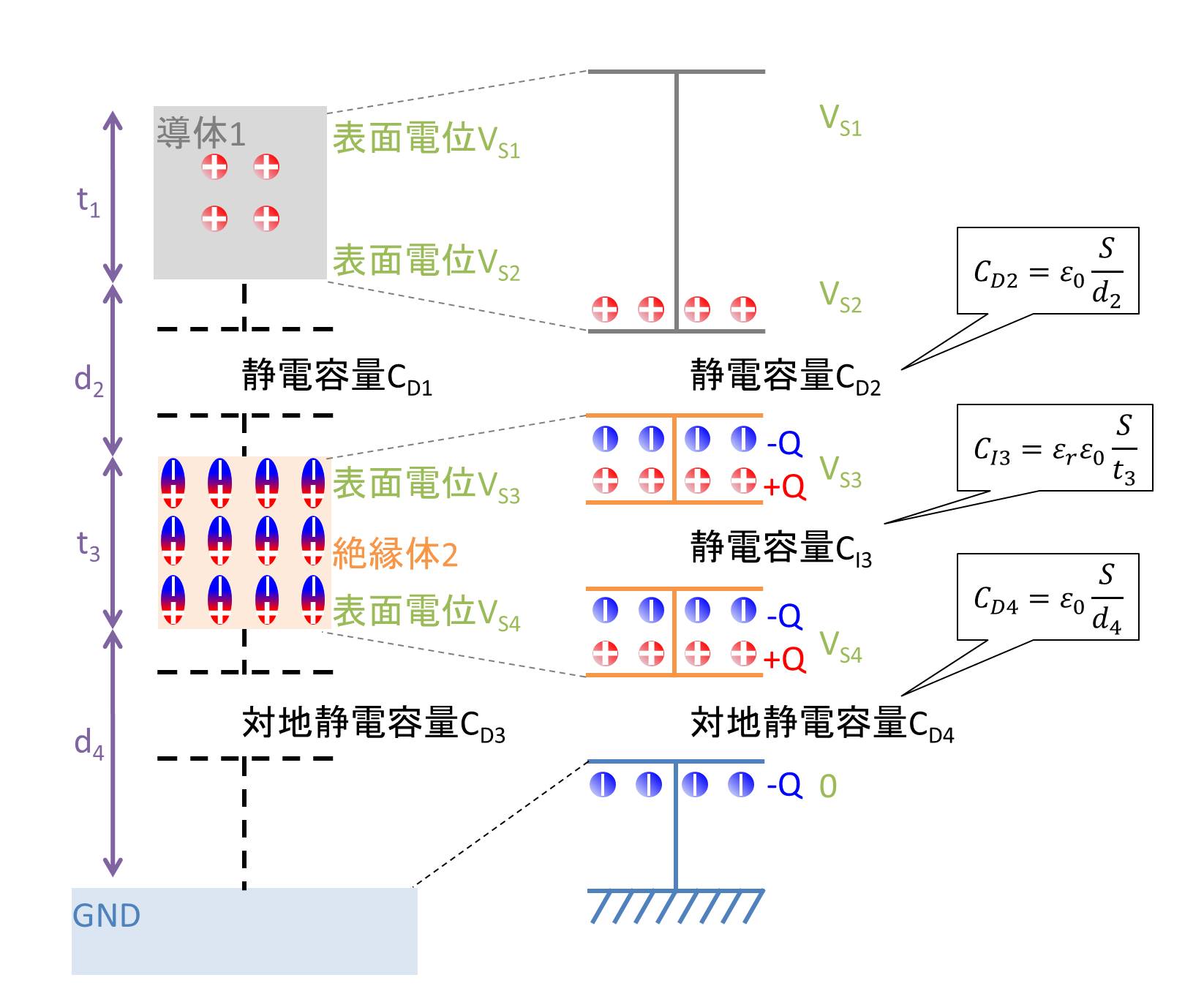
となります。例として導体1の表面電位VS1, VS2が1000V、物体の厚さがt1= t3=50cm、d2とd4の距離の和が100cmの時に絶縁体2を上下に移動させた時の各表面電位をグラフに示します。このように、帯電物体との距離が0cmの時、絶縁体2の表面電位VS3が1000Vとなります。そこから線形的に減少していくことがわかります。また、絶縁体2で生じる電位差VS3- VS4が一定であることも読み取れます。
帯電絶縁体→導体→GNDの場合
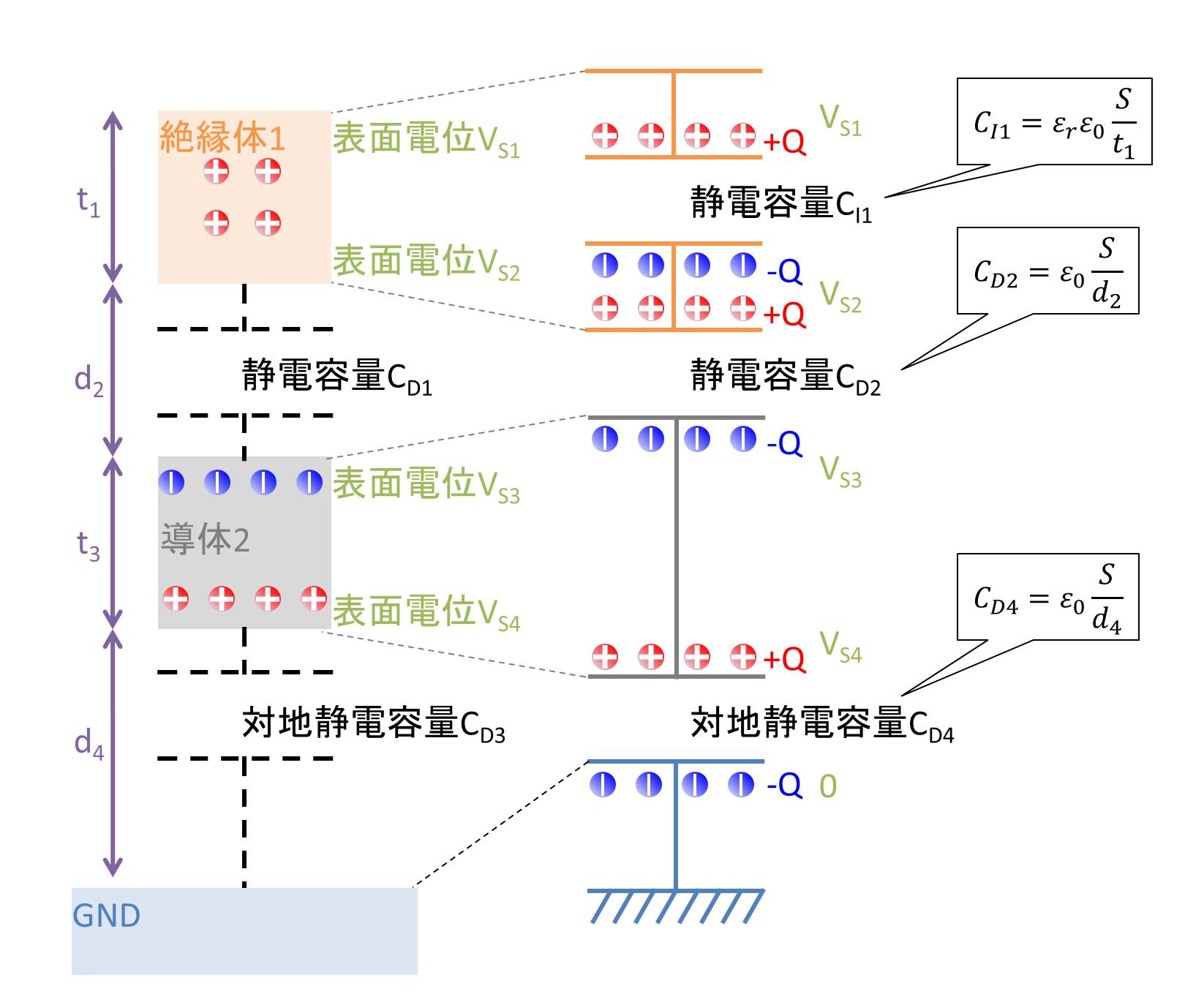
上部が絶縁体で中心の物体が導体の場合です。これはこのような図になります。
絶縁体1の厚さをt1、導体2の厚さをt3、絶縁体1と導体2の距離をd2、導体2とGNDとの距離をd4とします。この時、導体2の表面電位は等しいため、VS3=VS4となります。
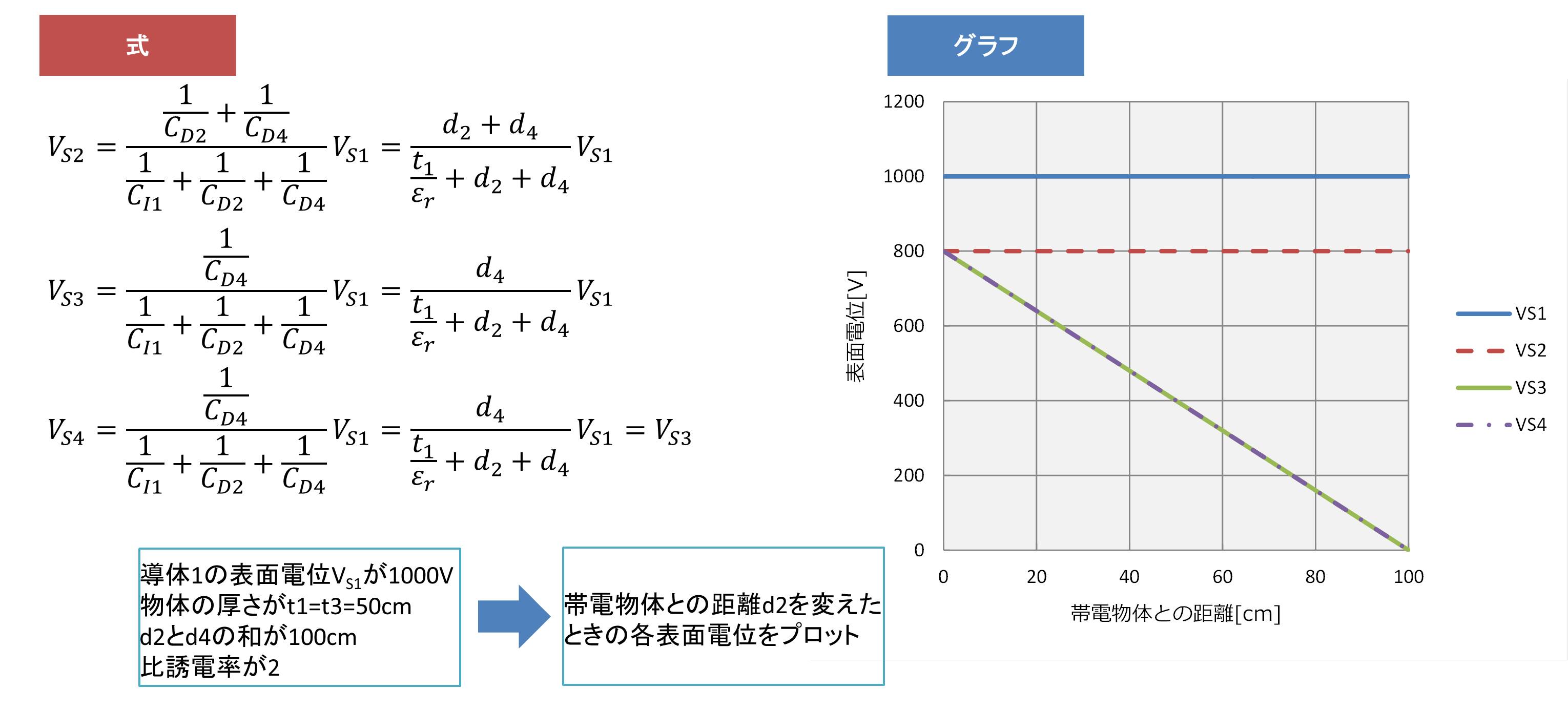
導体2は帯電絶縁体1と同じ極性の電位を持ちます。絶縁体1の表面電位VS2は、絶縁体1内部の静電容量CI1、帯電絶縁体1と導体2の静電容量CD2と導体2の対地静電容量CD4の分圧となるため、
$$ V_{S2} = \frac{\frac{1}{ C_{D2}}+\frac{1}{ C_{D4}}}{\frac{1}{ C_{I1}}+\frac{1}{ C_{D2}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{d_2}+{d_4}}{{\frac{t_1}{\varepsilon_r}}+{d_2}+{d_4}} V_{S1}$$
同様に、導体2の表面電位VS3, VS4は
$$ V_{S3} = V_{S4} =\frac{\frac{1}{ C_{D4}}}{\frac{1}{ C_{I1}}+\frac{1}{ C_{D2}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{d_4}}{{\frac{t_1}{\varepsilon_r}}+{d_2}+{d_4}} V_{S1}$$
となります。例として絶縁体1の表面電位VS1が1000V、物体の厚さがt1= t3=50cm、d2とd4の距離の和が100cmの時に導体2を上下に移動させた時の各表面電位をグラフに示します。
帯電絶縁体→絶縁体→GNDの場合

上部が絶縁体で中心の物体も絶縁の場合です。これが一番難しいです。
絶縁体1の厚さをt1、絶縁体2の厚さをt3、絶縁体1と絶縁体2の距離をd2、導体2とGNDとの距離をd4とします。
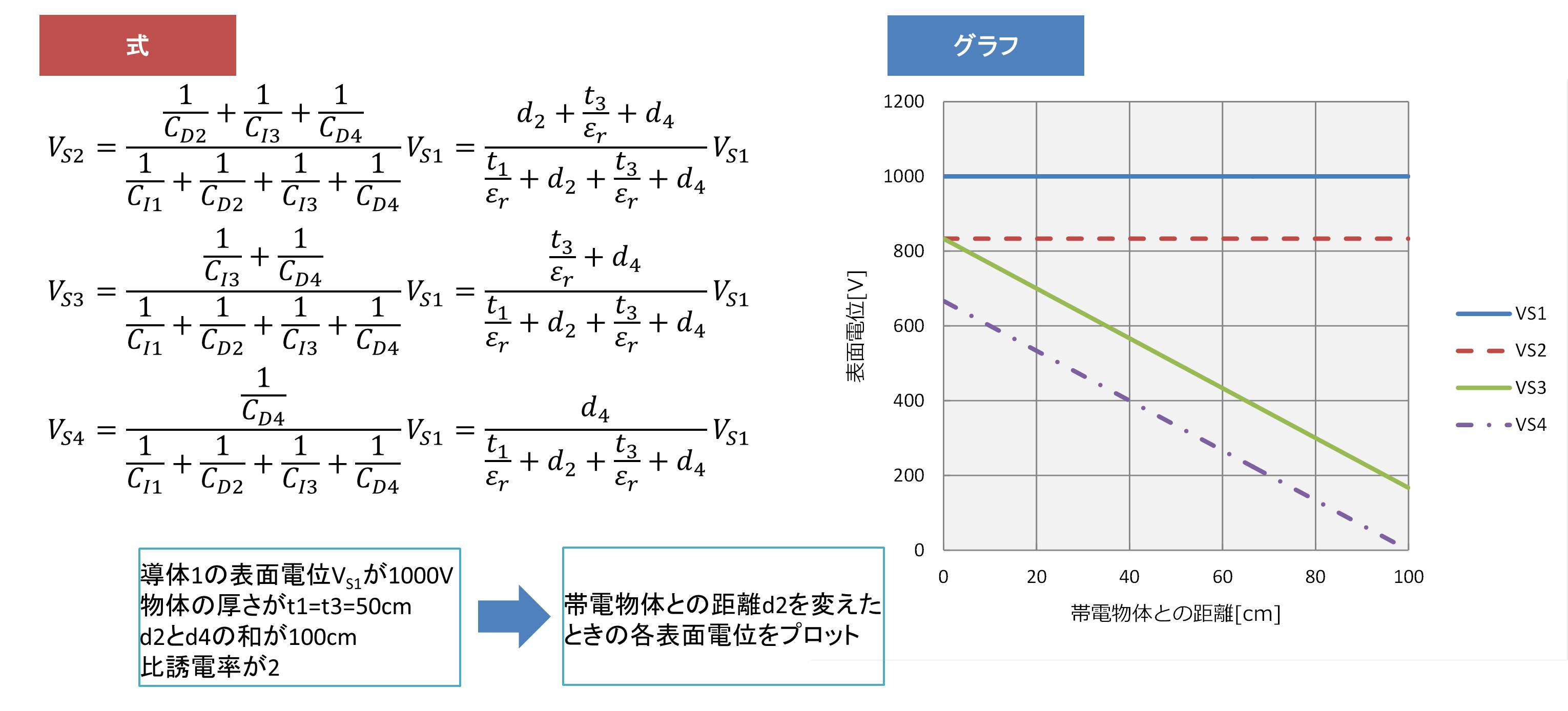
絶縁体2は帯電絶縁体1と同じ極性の電位を持ちます。絶縁体1の表面電位VS2は、絶縁体1内部の静電容量CI1、帯電絶縁体1と絶縁体2の静電容量CD2、絶縁体2内部の静電容量CI3、絶縁体2の対地静電容量CD4の分圧となるため、
$$ V_{S2} = \frac{\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}}{\frac{1}{ C_{I1}}+\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}}{{\frac{t_1}{\varepsilon_r}}+{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}} V_{S1}$$
同様に、
$$ V_{S3} = \frac{\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}}{\frac{1}{ C_{I1}}+\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{\frac{t_3}{\varepsilon_r}}+{d_4}}{{\frac{t_1}{\varepsilon_r}}+{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}} V_{S1}$$
$$ V_{S4} = \frac{\frac{1}{ C_{D4}}}{\frac{1}{ C_{I1}}+\frac{1}{ C_{D2}}+\frac{1}{ C_{I3}}+\frac{1}{ C_{D4}}} V_{S1} = \frac{{d_4}}{{\frac{t_1}{\varepsilon_r}}+{d_2}+{\frac{t_3}{\varepsilon_r}}+{d_4}} V_{S1}$$
となります。例として絶縁体1の表面電位VS1が1000V、物体の厚さがt1= t3=50cm、d2とd4の距離の和が100cmの時に絶縁体2を上下に移動させた時の各表面電位をグラフに示します。
なお、絶縁体の位置が変わっても全体の合成容量は変化しないため、絶縁体の位置を変えることで表面電位が変わることはありません。しかし、絶縁体が入ると容量が変化するため、表面電位が変わってしまいます。
導体を除電させた場合
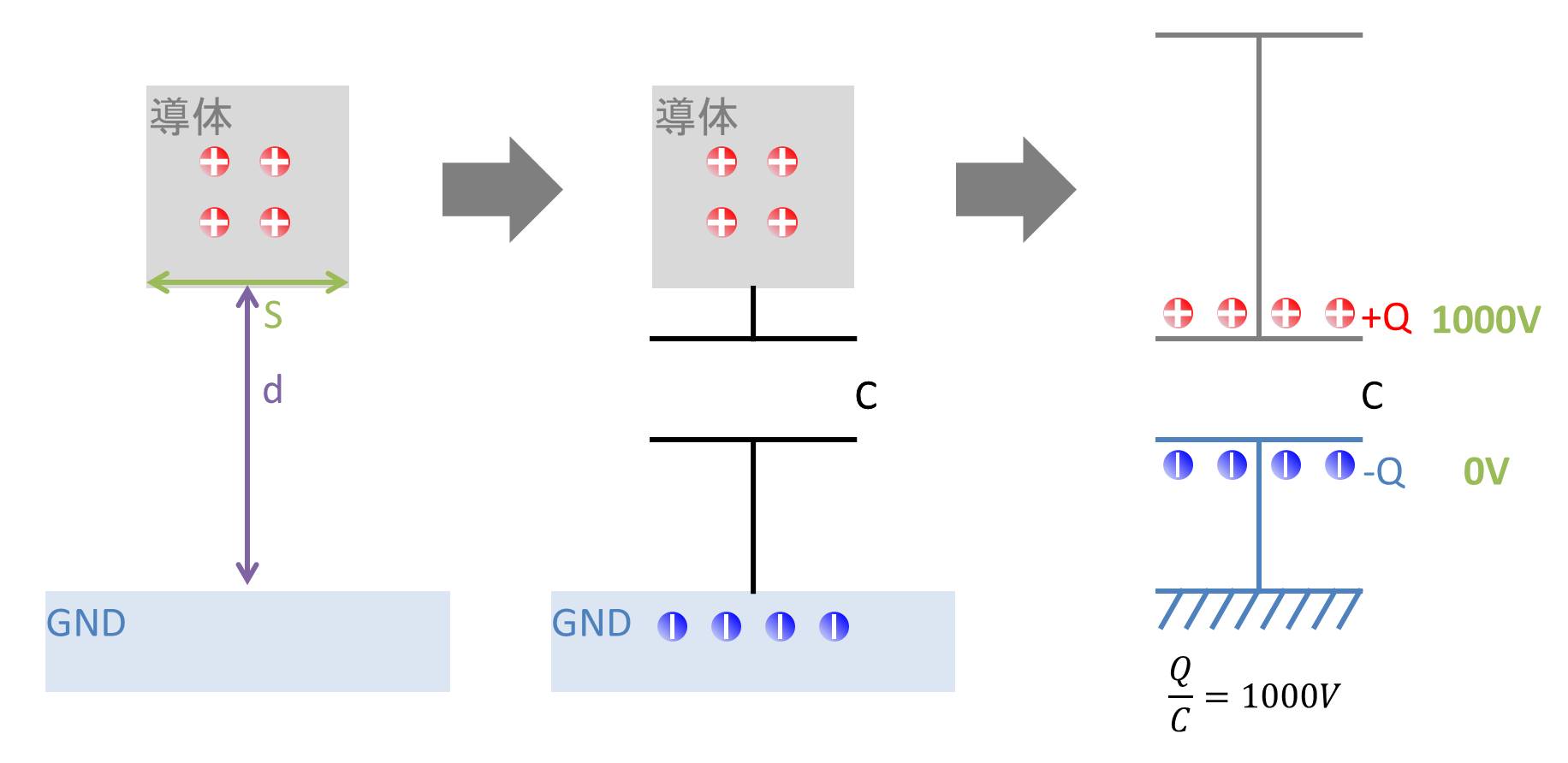
図のように1000Vに帯電している孤立導体があるとします。孤立導体とGNDとの間には対地静電容量Cがあります。
■帯電させた側を除電した場合
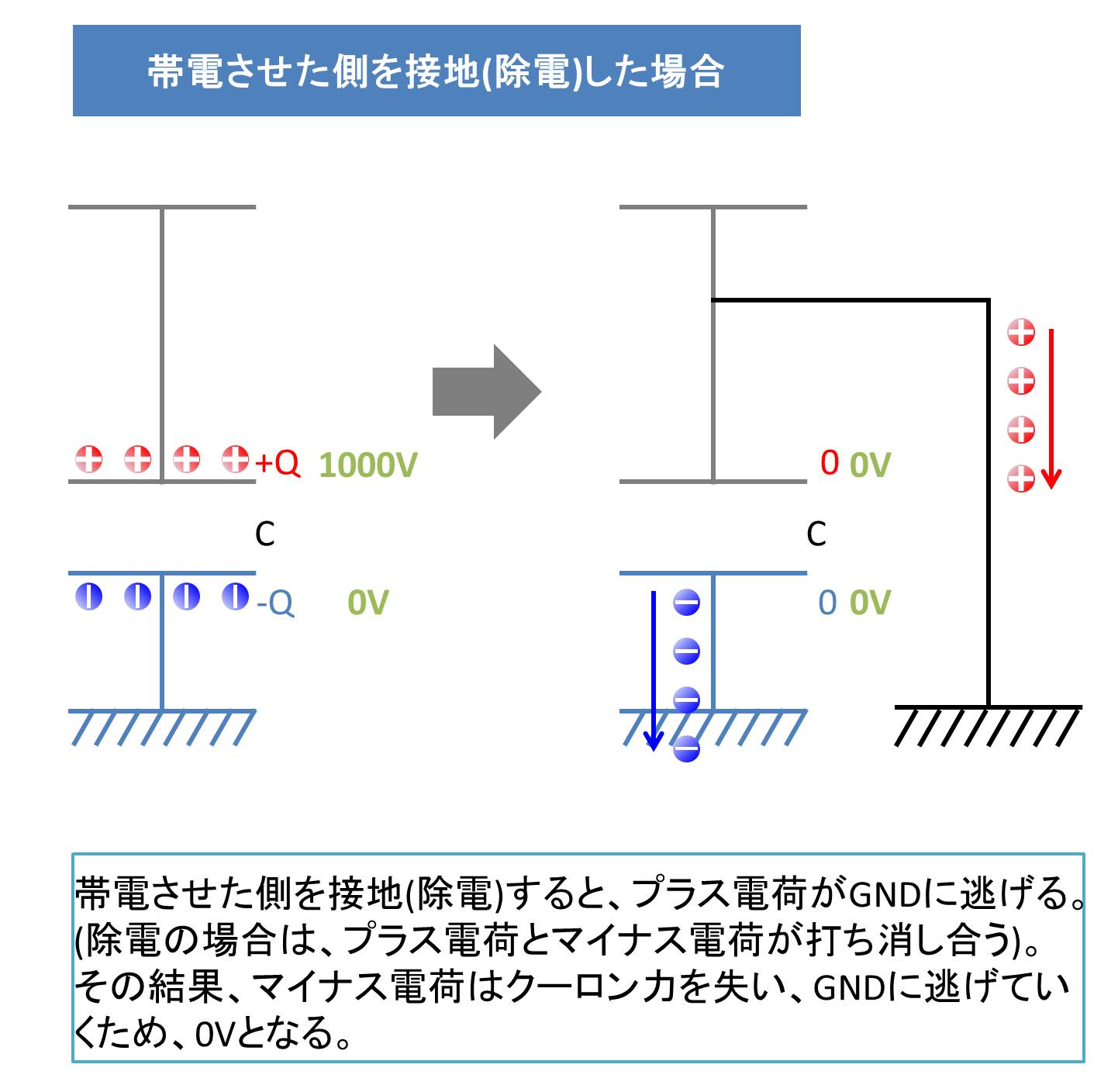
マイナス電荷がプラス電荷の方へいき、プラス電荷とマイナス電荷が打ち消し合います。その結果、GNDに存在していたマイナス電荷はプラス電荷によって生じていたクーロン力による引力を失い、GNDに流れます。最終的に導体とGND間に存在する対地静電容量に蓄えられている電荷がなくなり、0Vとなります。
■帯電させてない側を除電した場合
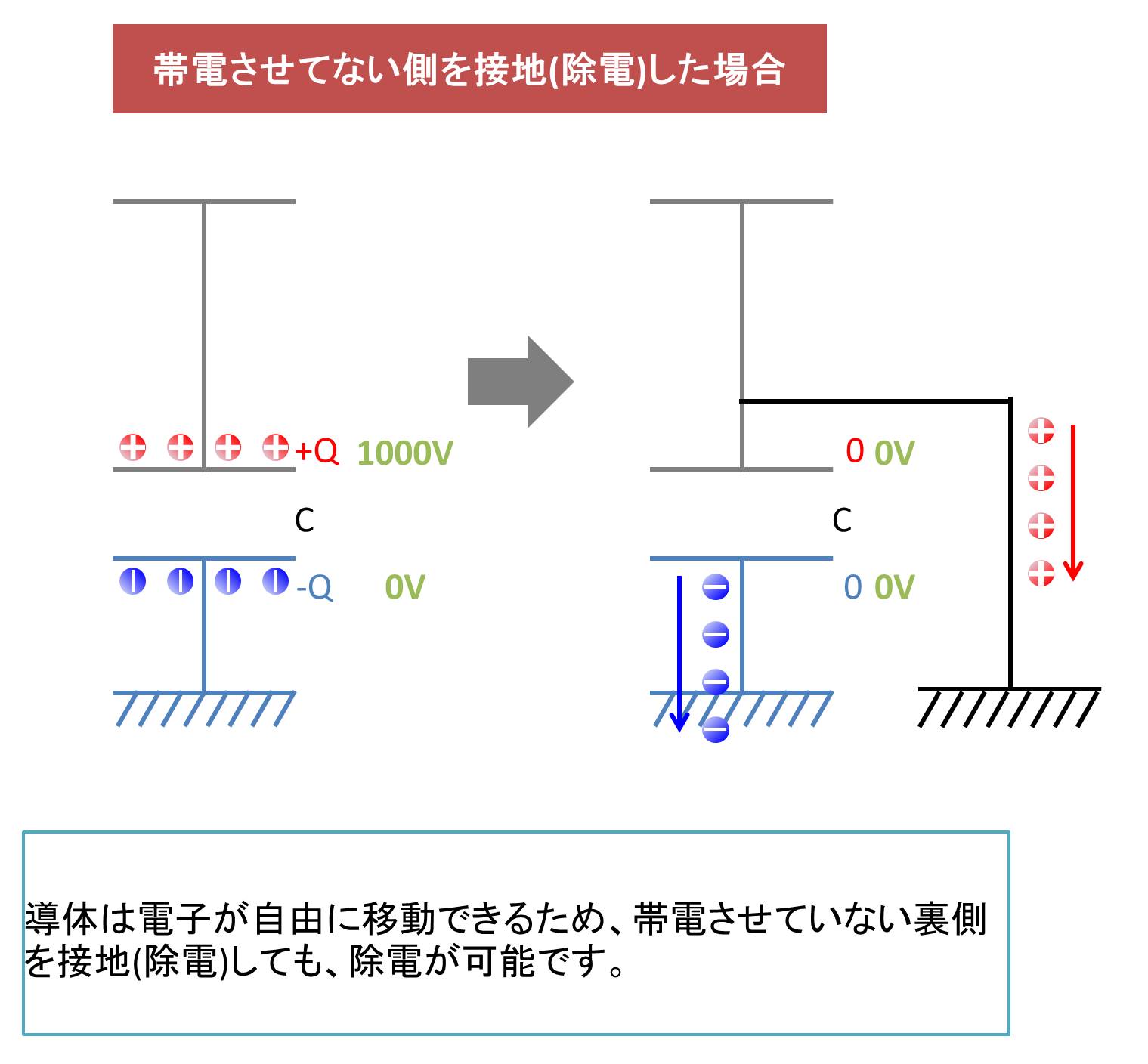
導体は電子が自由に移動できるため、帯電させていない裏側を除電しても除電が可能です。
絶縁体を除電させた場合
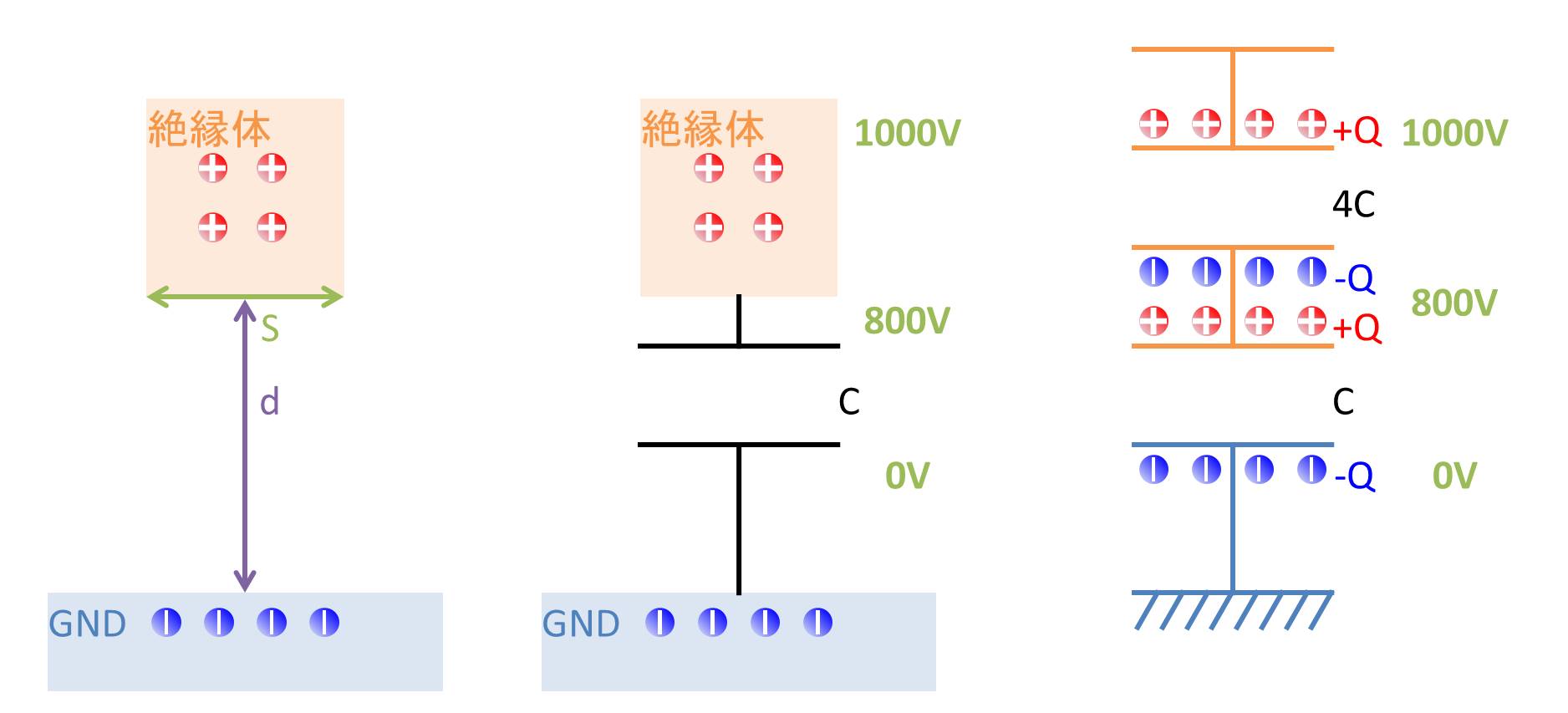
図のように1000Vに帯電している孤立導体があるとします。孤立絶縁体とGNDとの間には対地静電容量Cがあります。絶縁体は電場が通るため電位差が存在します。帯電させた時、絶縁体の上面が1000V、絶縁体の下面が800Vだった場合、対地静電容量をCとすると、絶縁体の静電容量は4Cとなります。
■帯電させた側を接地した場合
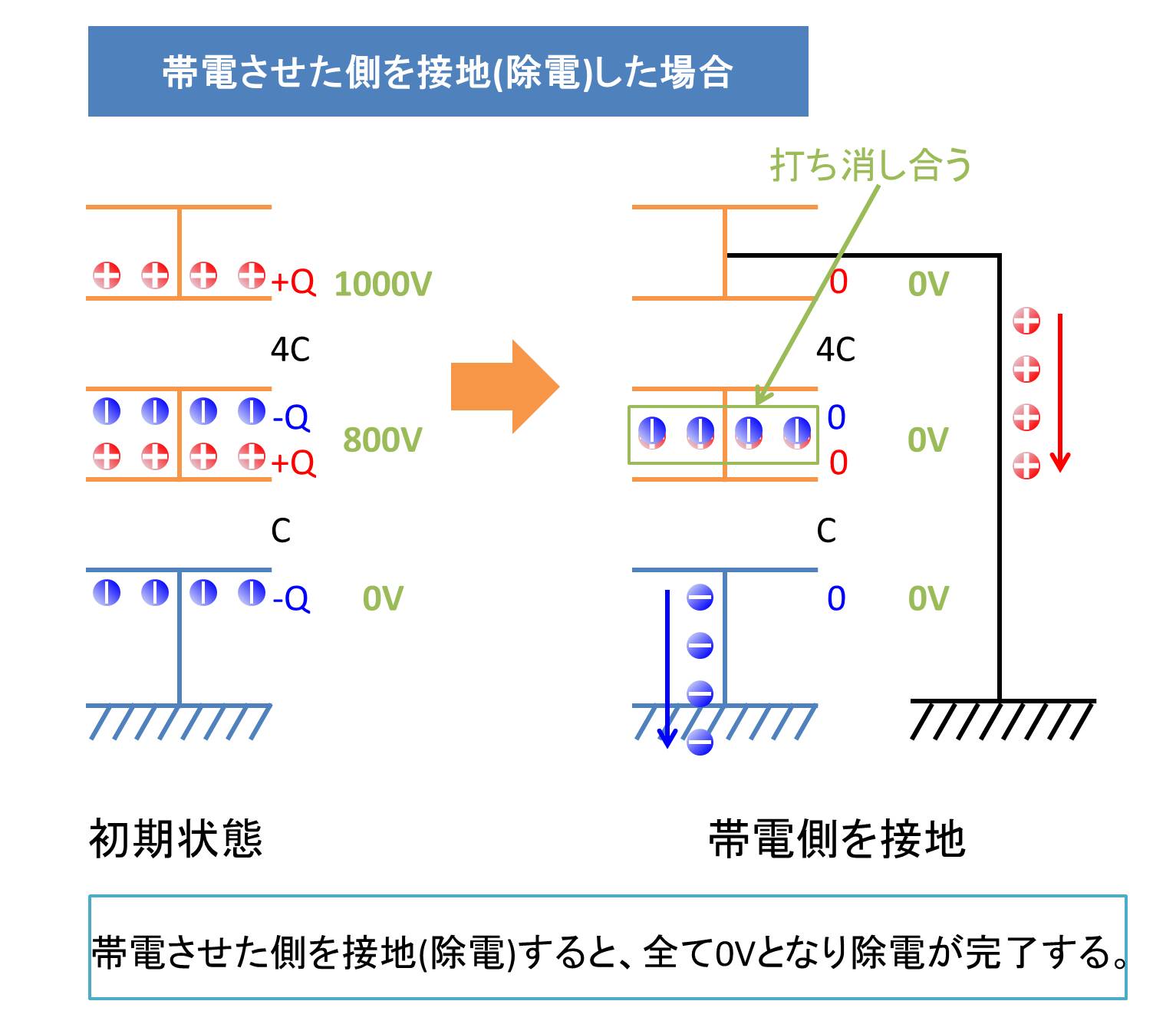
マイナス電荷がプラス電荷の方へいき、プラス電荷とマイナス電荷が打ち消し合います。その結果、絶縁体の静電容量と対地静電容量に存在する電荷はお互いに打ち消し合い消失し、GNDに存在していたマイナス電荷はプラス電荷によって生じていたクーロン力による引力を失い、GNDに流れます。最終的に表面電位はすべて0Vとなり、除電が正常に完了します。
■帯電させてない側を除電した場合
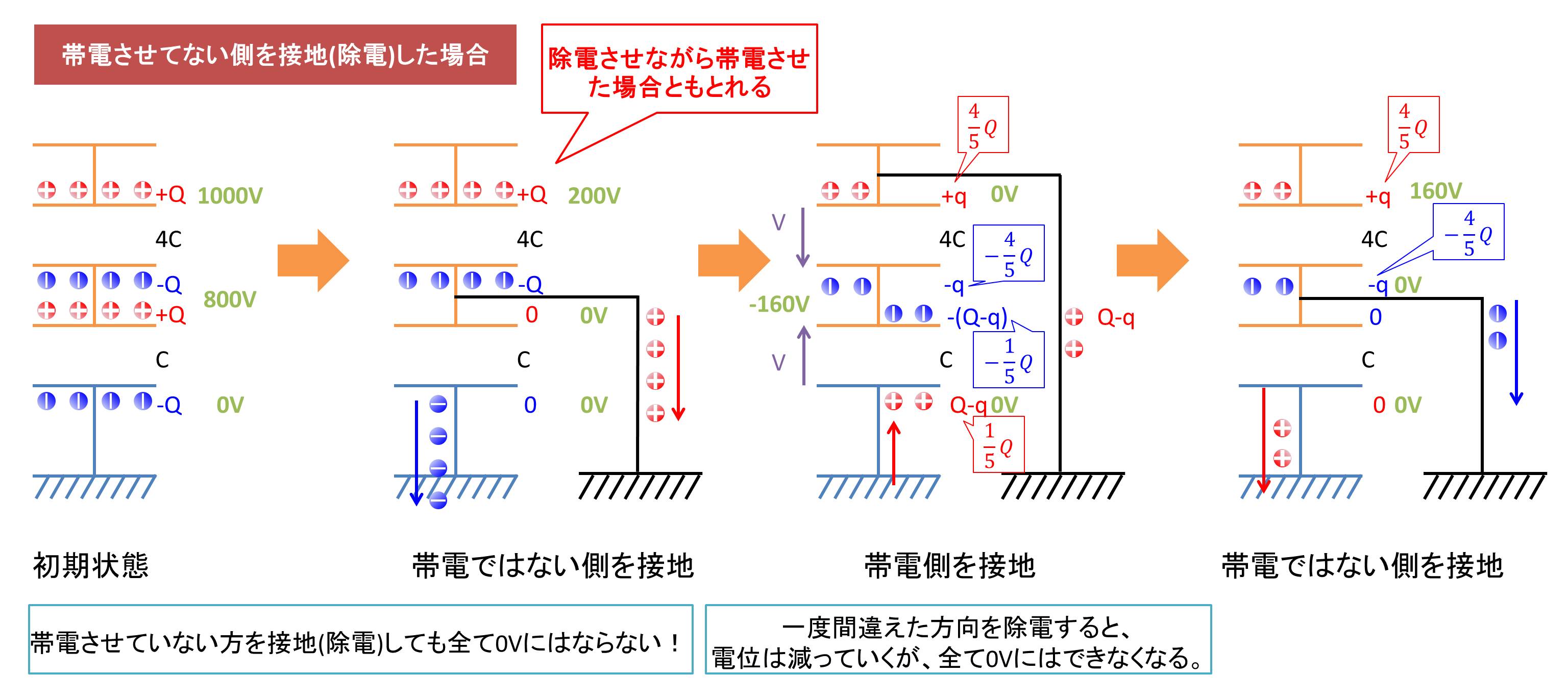
この場合は全てを0Vにすることができません。
詳しく説明します。帯電させてない側を除電すると、マイナス電荷がプラス電荷の方へいくことで、プラス電荷とマイナス電荷が打ち消し合います(プラス電荷が出ていくともいえる)。その結果、GNDに存在していたマイナス電荷はプラス電荷によって生じていたクーロン力による引力を失い、GNDに流れます。しかし、絶縁体上面にはまだ電荷Qが存在するため、除電しているにも関わらず、除電できていない方には表面電位が現れます。次に帯電している側を除電してみます。この場合、絶縁体上面は0Vになりますが、絶縁体上面に存在する電荷は全て除電できません。それは対地静電容量に存在するマイナス電荷があるからです。除電した側も0V、GNDも0Vですが、対地静電容量に存在するマイナス電荷は逃げ場がないため、電位差が等しくなるように電荷が移動します。その結果、GNDにはプラス電荷が現れます。
除電させながら帯電させ放置すると・・・
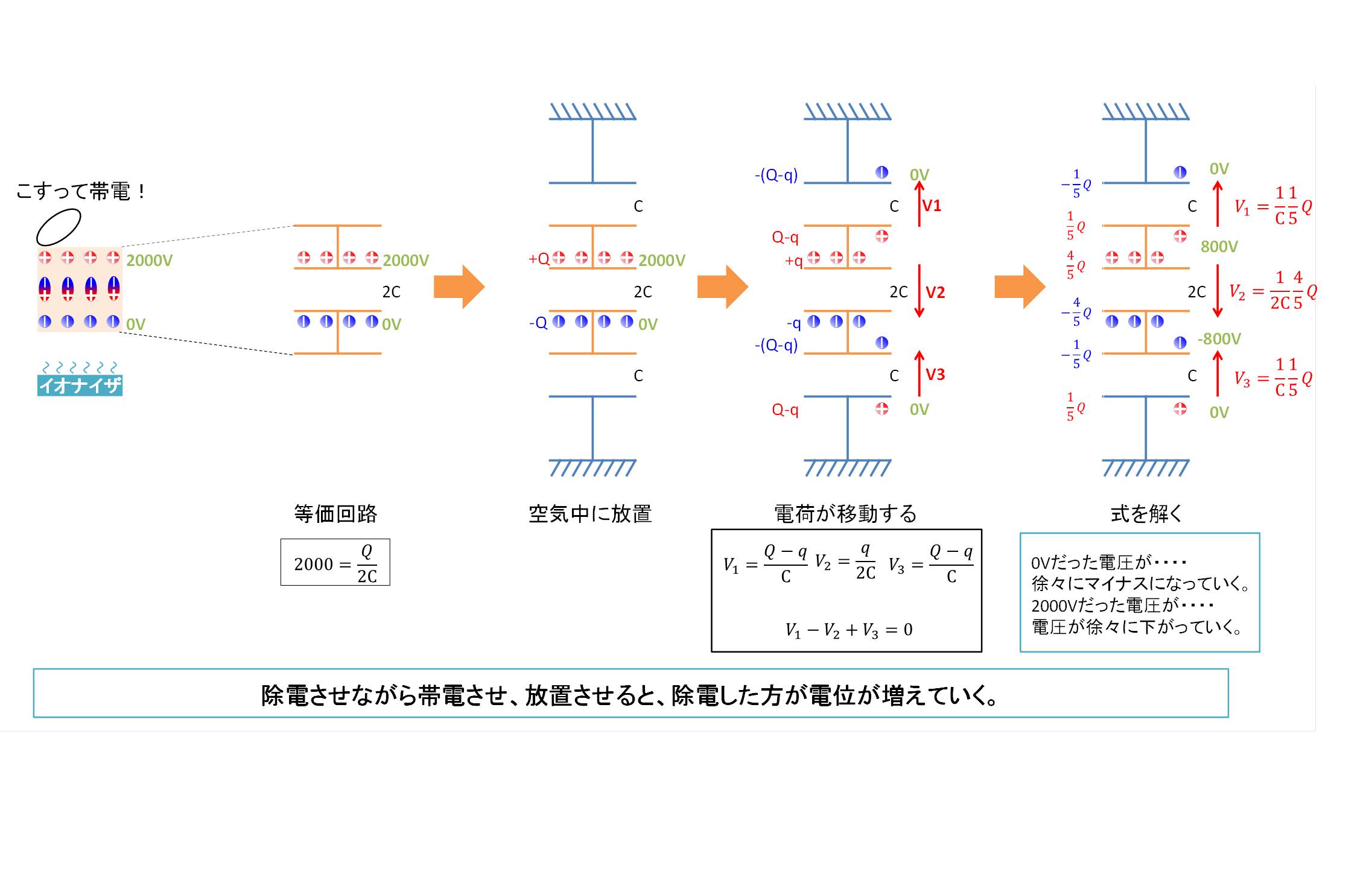
除電させながら帯電させ放置すると、電位が増加していくような現象が生じることがあります。例えば、イオナイザを当てている個所と異なる個所が擦られ帯電しているような構成や、帯電させている方の反対側が金属部でその金属部に触れることがあるような構成で生じます。
今回、例としてイオナイザを当てている個所と反対の面が2000Vに帯電してしまっていると想定します。絶縁体の容量を2Cとし、溜まっている電荷量をQとすると、
$$ Q= 2C×2000$$
となります。
その状態でイオナイザをOFFして放置をすると、絶縁体上面と下面には対地静電容量Cが接続されます。すると、絶縁体にたまっていた電荷量Qはキルヒホッフの法則を満たすように移動します。今回、絶縁体に残る電荷量をqとすると、
$$ V_1= \frac{Q-q}{C}$$
$$ V_2= \frac{q}{2C}$$
$$ V_3= \frac{ Q-q }{2C}$$
$$ V_1-V_2-V_3= 0$$
となります。式を解くと、
$$ q = \frac{4}{5}Q$$
$$ V_1= V_3=800 [V]$$
$$ V_2= 1600 [V]$$
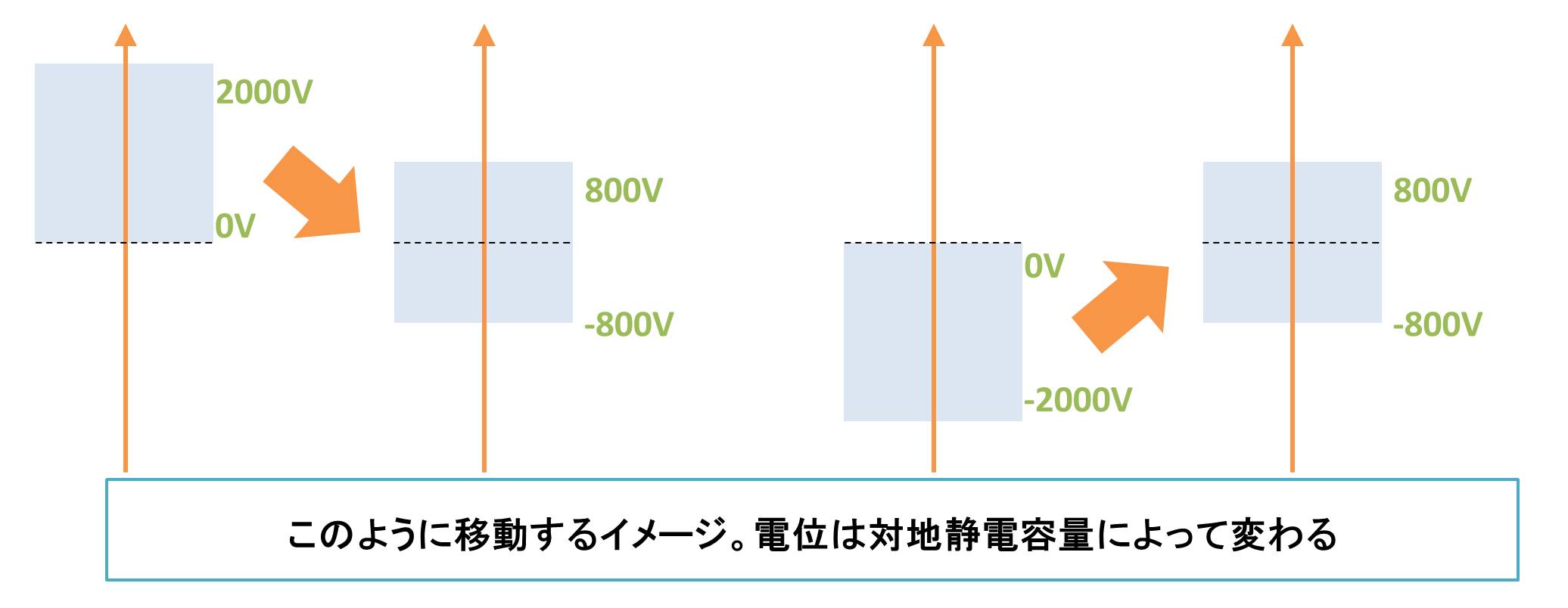
となります。このように、除電させながら帯電させたり、帯電させた後に間違えた方向を除電する等を行うと、0Vになっていた電位がどんどん上がっていってしまうのです。イメージはこのような感じです。
今回の例では、最終的に収まる電位が800Vと-800Vになり、電位の絶対値が等しくなりました。しかし、これは対地静電容量によって異なり、絶縁体上面と下面の対地静電容量が異なっている場合では電位の絶対値は等しくなりません。