この記事では『SI接頭語』について
- SI接頭語とは
- SI接頭語の『覚え方』・『一覧表』・『変換方法』・『ルール』・『例題』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
SI接頭語とは

SI接頭語とは、大きな桁や小さな桁を表すために、単位の前に付けられている接頭語です。
身近な例としては、距離を表す単位の「mm(ミリメートル)」の「m(ミリ)」、「cm(センチメートル)」の「c(センチ)」、「km(キロメートル)」の「k(キロ)」などがSI接頭語となります。
「m(ミリ)」、「c(センチ)」、「k(キロ)」どれも単位「m(メートル)」の前に付けられていますね。
これらSI接頭語は「10■」を表しています(■には数字が入ります)。
例えば、SI接頭語の「k(キロ)」は「103」を表しています。そのため、「1km」の「km」を「m」に変換する場合には、次式のように変換します。
\begin{eqnarray}
1{\mathrm{km}}=1×10^3{\mathrm{m}}=1000{\mathrm{m}}
\end{eqnarray}
同様に、「c(センチ)」は「10-2」を表しています。そのため、「1cm」の「cm」を「m」に変換する場合には、次式のように変換します。
\begin{eqnarray}
1{\mathrm{cm}}=1×10^{-2}{\mathrm{m}}=10^{-2}{\mathrm{m}}=0.01{\mathrm{m}}
\end{eqnarray}
SI接頭語は全部で20個もあります。次に「SI接頭語の一覧」について説明します。
補足
- SI接頭語は「SI接頭辞」や、SIを付けずに単に「接頭語」や「接頭辞」とも呼ばれています。
ポイント:コンデンサの静電容量
電気の世界では、コンデンサの静電容量の単位である「μF(マイクロファラド)」の「μ(マイクロ)」や「pF(ピコファラド)」の「p(ピコ)」もSI接頭語になります。「μ(マイクロ)」と「p(ピコ)」どれも単位「F(ファラド)」の前に付けられていますね。
SI接頭語の一覧
SI接頭語は「10■」を表しており、全部で20個あることを説明しました。
これら20個のSI接頭語のうち、1番大きな桁は「Y(ヨタ)」の「1024」、1番小さな桁は「y(ヨクト)」の「10-24」まであります。
各SI接頭語の記号・名称・数値・十進表記・和名をまとめた一覧表を下記に示します。
| 記号 | 名称 | 数値 | 十進表記 | 和名 |
| Y | ヨタ(yotta) | 1024 | 1,000,000,000,000,000,000,000,000 | じょ、秭(し) |
| Z | ゼタ(zetta) | 1021 | 1,000,000,000,000,000,000,000 | 十垓(がい) |
| E | エクサ(exa) | 1018 | 1,000,000,000,000,000,000 | 百京(けい) |
| P | ペタ(peta) | 1015 | 1,000,000,000,000,000 | 千兆 |
| T | テラ(tera) | 1012 | 1,000,000,000,000 | 兆 |
| G | ギガ(giga) | 109 | 1,000,000,000 | 十億 |
| M | メガ(mega) | 106 | 1,000,000 | 百万 |
| k | キロ(kilo) | 103 | 1,000 | 千 |
| h | ヘクト(hecto) | 102 | 100 | 百 |
| da | デカ(deca) | 101 | 10 | 十 |
| 100 | 1 | 一 | ||
| d | デシ(deci) | 10-1 | 0.1 | 分(ぶ) |
| c | センチ(centi) | 10-2 | 0.01 | 厘(りん) |
| m | ミリ(milli) | 10-3 | 0.001 | 毛(もう) |
| μ | マイクロ(micro) | 10-6 | 0.000 001 | 微(び) |
| n | ナノ(nano) | 10-9 | 0.000 000 001 | 塵(じん) |
| p | ピコ(pico) | 10-12 | 0.000 000 000 001 | 漠(ばく) |
| f | フェムト(femto) | 10-15 | 0.000 000 000 000 001 | 須臾(しゅゆ) |
| a | アト(atto) | 10-18 | 0.000 000 000 000 000 001 | 刹那(せつな) |
| z | ゼプト(zepto) | 10-21 | 0.000 000 000 000 000 000 001 | 清浄(せいじょう) |
| y | ヨクト(yocto) | 10-24 | 0.000 000 000 000 000 000 000 001 | 涅槃寂静(ねはんじゃくじょう) |
これらSI接頭語のうち、「記号」と「数値」の関係を覚えておいた方が良いものは赤色と緑色で示しています。後ほど覚え方について説明します。
SI接頭語はラテン語やギリシャ語が由来となっています。例えば、「m(ミリ)」や「c(センチ)」はラテン語の「milli(1000)」や「centum(100)」が由来であり、「k(キロ)」はギリシャ語の「khilioi(1000)」が由来となっています。
SI接頭語の覚え方
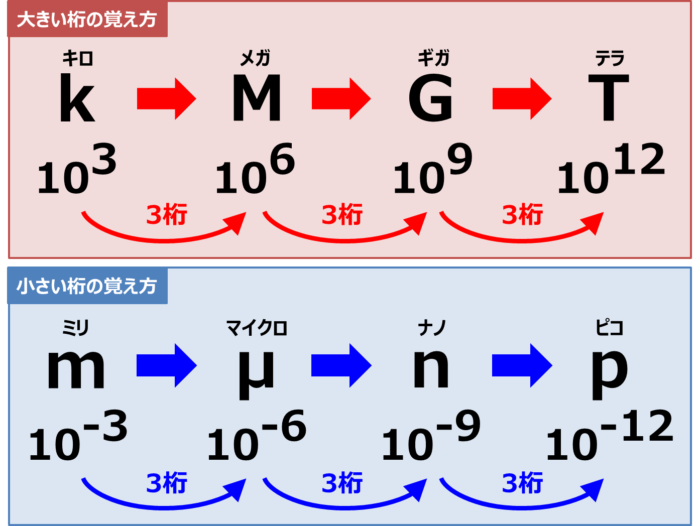
SI接頭語は「3桁ずつずれていくことに着目する」と覚えやすいです。
大きい桁の覚え方
「k(103)」→「M(106)」→「G(109)」→「T(1012)」
と3桁ずつずれていくことに着目して、「キロ、メガ、ギガ、テラ」と何回も声に出して覚えます。
「k(キロ)」が「103」であることだけを覚えて置けば、「M(メガ)」は「k(キロ)」から3桁ずれるので、「106」だと分かります。
「h(ヘクト)」だけは別途「102」と暗記します。
小さい桁の覚え方
「m(10-3)」→「μ(10-6)」→「n(10-9)」→「p(10-12)」
と3桁ずつずれていくことに着目して、「ミリ、マイクロ、ナノ、ピコ」と何回も声に出して覚えます。
「m(ミリ)」が「10-3」であることだけを覚えて置けば、「μ(マイクロ)」は「m(ミリ)」から3桁ずれるので、「10-6」だと分かります。
「d(デシ)」は「10-1」、「c(センチ)」は「10-2」と別途暗記します。
SI接頭語のルール
SI接頭語を使う上で、いくつかルールがあるので、これから説明します。
ルール1:大文字と小文字を分けること

大文字のSI接頭語は小文字にはしてはいけません。同様に、小文字のSI接頭語は大文字にはしてはいけません。
例えば、「m(ミリ)」(←10-3)を大文字にしてしまうと「M(メガ)」(←106)になってしまいます・
ルール2:2つのSI接頭語を組み合わせてはいけない
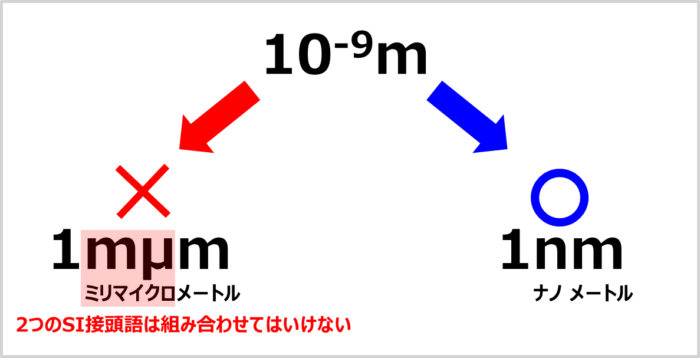
SI接頭語は組み合わせてつかうことはできません。
例えば、10-9mを次式に示すように変換してはいけないということです。
\begin{eqnarray}
10^{-9}{\mathrm{m}}=1×10^{-3}×10^{-6}{\mathrm{m}}=1{\mathrm{mμm}}
\end{eqnarray}
10-9mを変換するためには「10-9」を表す「n(ナノ)」を用いて、次式のように変換します。
\begin{eqnarray}
10^{-9}{\mathrm{m}}=1×10^{-9}{\mathrm{m}}=1{\mathrm{nm}}
\end{eqnarray}
ルール3: SI接頭語は累乗よりも優先である
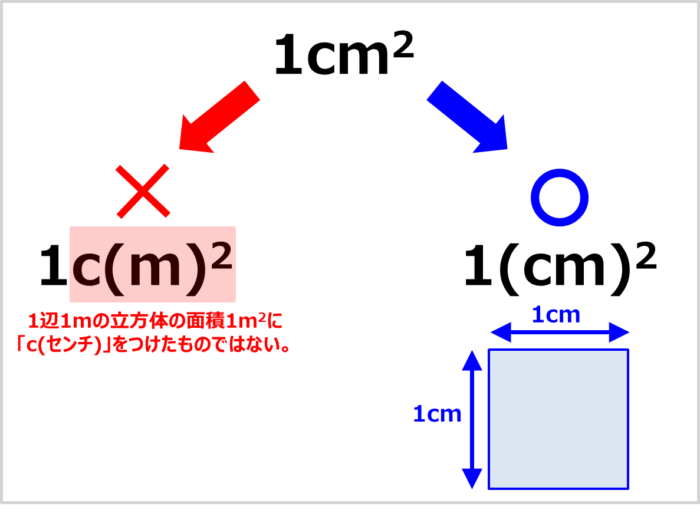
例えば、面積1cm2は1辺1cmの正方形の面積であり、
\begin{eqnarray}
1{\mathrm{cm}}×1{\mathrm{cm}}&=&1{\mathrm{(cm)^2}}\\
&=&1{\mathrm{cm^2}}\\
\\
1{\mathrm{cm}}×1{\mathrm{cm}}&=&1×10^{-2}{\mathrm{m}}×1×10^{-2}{\mathrm{m}}\\
&=&1×10^{-4}{\mathrm{m^2}}\\
\end{eqnarray}
となるため、「1cm2」は「1m2を10-4倍したもの」と等しくなります。
1辺1mの正方形の面積1m2に「c(センチ)」をつけたものではないので注意してください。
SI接頭語の例題
例題
1kmは「何m」「何cm」「何mm」でしょうか。
解答
kmをmに変換する方法
kmの「k(キロ)」がSI接頭語であり、「103」を表しています。そのため、1kmをmに変換するには次式のように計算します。
\begin{eqnarray}
1{\mathrm{km}}=1×10^3{\mathrm{m}}=1000{\mathrm{m}}
\end{eqnarray}
kmをcmに変換する方法
cmの「c(センチ)」がSI接頭語であり、「10-2」を表しています。そのため、1kmをcmに変換するには次式のように計算します。
\begin{eqnarray}
1{\mathrm{km}}=1×10^3{\mathrm{m}}=1×10^5×10^{-2}{\mathrm{m}}=1×10^5{\mathrm{cm}}=100000{\mathrm{cm}}
\end{eqnarray}
kmをmmに変換する方法
mmの「m(ミリ)」がSI接頭語であり、「10-3」を表しています。そのため、1kmをmmに変換するには次式のように計算します。
\begin{eqnarray}
1{\mathrm{km}}=1×10^3{\mathrm{m}}=1×10^6×10^{-3}{\mathrm{m}}=1×10^6{\mathrm{mm}}=1000000{\mathrm{mm}}
\end{eqnarray}
まとめ
この記事では『SI接頭語』について、以下の内容を説明しました。
- SI接頭語とは
- SI接頭語の『覚え方』・『一覧表』・『変換方法』・『ルール』・『例題』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。






