この記事では『片対数グラフ』と『両対数グラフ』について
- 対数グラフの種類
- 『片対数グラフ』とは
- 『片対数グラフ』と『指数関数』の関係
- 『両対数グラフ』とは
- 『両対数グラフ』と『べき関数』の関係
などを図を用いて分かりやすく説明しています。
まず最初に・・・普通の目盛と対数目盛について
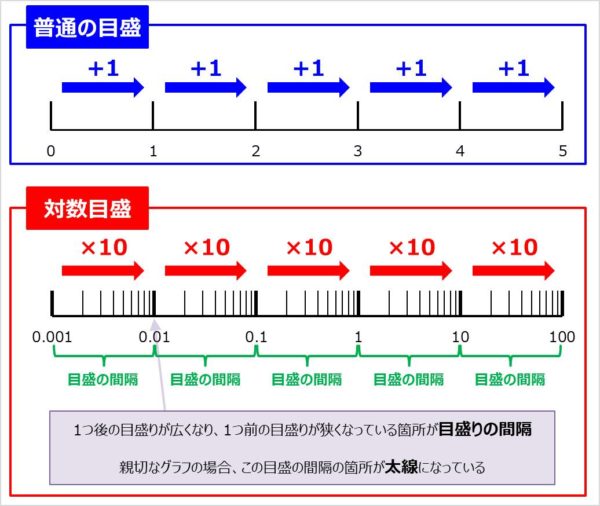
一般的によく見かける目盛は2点間の距離が0,1,2,3,4,5・・・のように数が1ずつ増えたり、0,10,20,30,40,50・・・のように数に10ずつ増えたりするような目盛となっています(この記事はこの目盛を普通の目盛と呼びます)。
一方、2点間の距離が0.001,0.01,0.1,1,10,100・・・のように数が10倍ずつ増えたりするような目盛を対数目盛と言います。対数目盛は1つ後の目盛りが広くなり、1つ前の目盛りが狭くなっている箇所が目盛りの間隔となっています。親切なグラフの場合、この目盛の間隔の箇所が太線になっています。
対数グラフの種類(片対数グラフと両対数グラフについて)
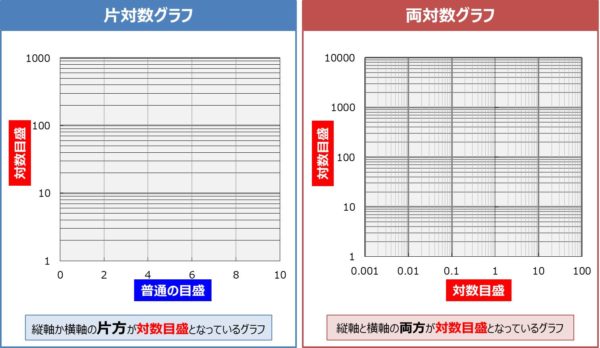
x軸かy軸が対数目盛となっているグラフのことを対数グラフといいます。対数グラフには片対数グラフと両対数グラフの2種類あります。
- 片対数グラフ
- 両対数グラフ
片対数グラフとは、「x軸:普通の目盛、y軸:対数目盛」や「x軸:対数目盛、y軸:普通の目盛」のようにx軸またはy軸の片方が対数目盛となっているグラフのことを指します。片対数グラフは英語では「Semi-Log Plot」または「Semi-Log Graph」と書きます。
両対数グラフとは、「x軸:対数目盛、y軸:対数目盛」のようにx軸とy軸の両方が対数目盛となっているグラフのことを指します。両対数グラフは英語では「Log-Log Plot」または「Log-Log Graph」と書きます。
補足
- 「x軸:対数目盛、y軸:普通の目盛」の片対数グラフはあまり見かけません。
- 「x軸:普通の目盛、y軸:普通の目盛」のグラフのことを方眼グラフといいます。
片対数グラフと指数関数の関係
片対数グラフで指数関数\((y=ca^x)\)を描くと直線となる
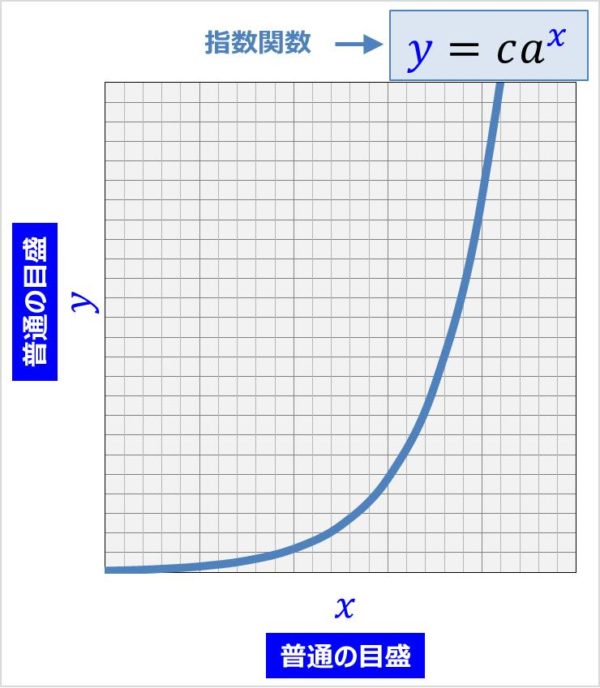
上図の指数関数 \(y=ca^x(c>0,a>0)\)は片対数グラフで描くと直線に、また縦軸を\({\log}_{10}y\)としても直線になります(直線になる理由は後ほど詳しく説明します)。
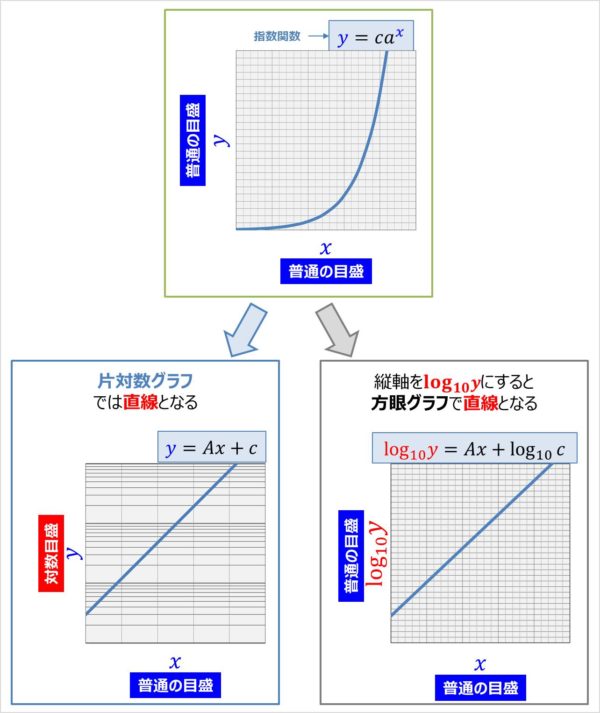
- 「x軸:普通の目盛、y軸:対数目盛」の片対数グラフの場合
- 「x軸:普通の目盛、y軸:普通の目盛」の方眼グラフの場合
直線\((y=Ax+c)\)になります。
縦軸を\({\log}_{10}y\)にすると、直線\(({\log}_{10}y=Ax+{\log}_{10}c)\)となります
指数関数\((y=ca^x)\)の\(a\)と\(c\)の求め方
まず、直線\((y=Ax+c)\)の傾き\(A\)を求める\(A\)
直線\((y=Ax+c)\)の2点\((x_1,y_1)\),\((x_2,y_2)\)を結んだ時の傾き\(A\)は以下の式で求めることができます。
\begin{eqnarray}
A=\frac{{\log}_{10}y_2-{\log}_{10}y_1}{x_2-x_1}
\end{eqnarray}
指数関数\(y=ca^x\)の底\(a\)を求める
直線\((y=Ax+c)\)の傾き\(A\)が分かると、指数関数\(y=ca^x\)の底\(a\)は以下の式で求めることができます。
\begin{eqnarray}
a=10^A
\end{eqnarray}
指数関数\(y=ca^x\)の\(c\)を求める
指数関数\((y=ca^x)\)の\(c\)は「x軸:普通の目盛、y軸:対数目盛」の片対数グラフにおける切片\(c\)と等しくなります。
指数関数が片対数グラフで直線になる理由
「x軸:普通の目盛、y軸:対数目盛」の片対数グラフについて、
- 指数関数\((y=ca^x)\)は片対数グラフでは直線\((y=Ax+c)\)になる理由
- 指数関数\((y=ca^x)\)の底\(a\)は\(a=10^A\)で求めることができる理由
- 指数関数\((y=ca^x)\)の\(c\)は片対数グラフにおける切片\(c\)と等しくなる理由
を説明します。
指数関数\((y=ca^x)\)の両辺に\({\log}_{10}\)を作用させると、
\begin{eqnarray}
{\log}_{10}y={\log}_{10}ca^x
\end{eqnarray}
となります。右辺を分解すると、
\begin{eqnarray}
{\log}_{10}y&=&{\log}_{10}a^x+{\log}_{10}c\\
{\Leftrightarrow}{\log}_{10}y&=&x{\log}_{10}a+{\log}_{10}c
\end{eqnarray}
となります。
ここで、
\begin{eqnarray}
{\log}_{10}a=A
\end{eqnarray}
と置くと、
\begin{eqnarray}
{\log}_{10}y&=&Ax+{\log}_{10}c
\end{eqnarray}
となります。上記の式を方眼グラフで描くと、直線となります。
また、片対数グラフにプロットするということは、方眼グラフでは\({\log}_{10}y\)を縦軸にとることと等しいため、片対数グラフの場合は以下の式となります。
\begin{eqnarray}
y&=&Ax+c
\end{eqnarray}
上式は直線の式であることが分かります。
また、直線\((y=Ax+c)\)の2点\((x_1,y_1)\),\((x_2,y_2)\)を結んだ時の傾き\(A\)は
\begin{eqnarray}
A=\frac{{\log}_{10}y_2-{\log}_{10}y_1}{x_2-x_1}
\end{eqnarray}
となります。ここで、\({\log}_{10}a=A\)を変形すると、
\begin{eqnarray}
a=10^A
\end{eqnarray}
となります。
したがって、指数関数\(y=ca^x\)の底\(a\)は上式で求めることができます。
また、直線\((y=Ax+c)\)より、指数関数\((y=ca^x)\)の\(c\)は切片\(c\)と等しくなることがわかります。
両対数グラフとべき関数の関係
両対数グラフでべき関数\((y=cx^a)\)を描くと直線となる
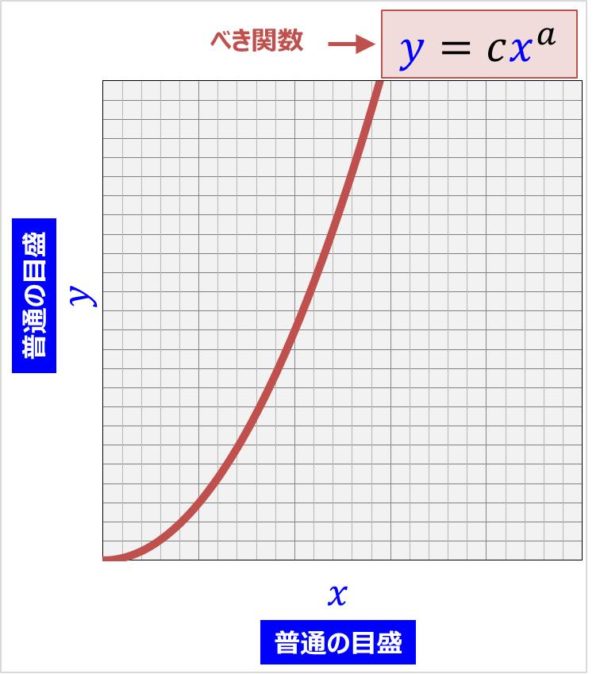
上図のべき関数\(y=cx^a(a>0)\)は両対数グラフで描くと直線に、また縦軸を\({\log}_{10}y\)、横軸を\({\log}_{10}x\)にしても直線になります(直線になる理由は後ほど詳しく説明します)。
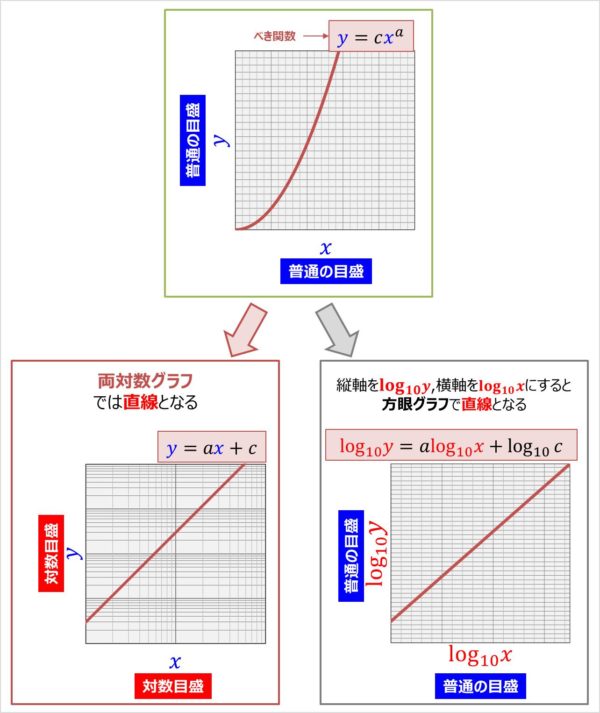
- 「x軸:対数目盛、y軸:対数目盛」の両対数グラフの場合
- 「x軸:普通の目盛、y軸:普通の目盛」の方眼グラフの場合
直線\((y=ax+c)\)になります。
縦軸を\({\log}_{10}y\)、横軸を\({\log}_{10}x\)にすると、直線\(({\log}_{10}y=A{\log}_{10}x+{\log}_{10}c)\)となります。
べき関数\((y=cx^a)\)の\(a\)と\(c\)の求め方
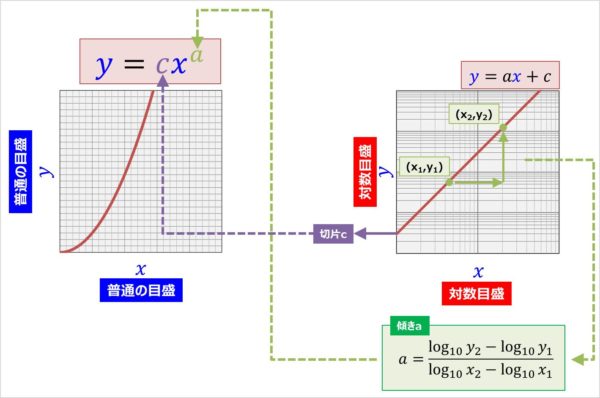
まず、直線\((y=ax+c)\)の傾き\(a\)を求める\(A\)
直線\((y=ax+c)\)の2点\((x_1,y_1)\),\((x_2,y_2)\)を結んだ時の傾き\(a\)は以下の式で求めることができます
\begin{eqnarray}
a=\frac{{\log}_{10}y_2-{\log}_{10}y_1}{{\log}_{10}x_2-{\log}_{10}x_1}
\end{eqnarray}
べき関数\((y=cx^a)\)のべき\(a\)を求める
べき関数\((y=cx^a)\)のべき\(a\)は直線の傾き\(a\)と等しくなります。
べき関数\((y=cx^a)\)の\(c\)を求める
べき関数\((y=cx^a)\)の\(c\)は「x軸:対数目盛、y軸:対数目盛」の両対数グラフにおける切片\(c\)と等しくなります。
べき関数が両対数グラフで直線になる理由
「x軸:対数目盛、y軸:対数目盛」の両対数グラフについて、
- べき関数\((y=cx^a)\)は両対数グラフでは直線\((y=ax+c)\)になる理由
- べき関数\((y=cx^a)\)のべき\(a\)は直線\((y=ax+c)\)の傾き\(a\)と等しくなる理由
- べき関数\((y=cx^a)\)の\(c\)は両対数グラフにおける切片\(c\)と等しくなる理由
を説明します。
べき関数\((y=cx^a)\)の両辺に\({\log}_{10}\)を作用させると、
\begin{eqnarray}
{\log}_{10}y={\log}_{10}cx^a
\end{eqnarray}
となります。右辺を分解すると、
\begin{eqnarray}
{\log}_{10}y&=&{\log}_{10}x^a+{\log}_{10}c\\
{\Leftrightarrow}{\log}_{10}y&=&a{\log}_{10}x+{\log}_{10}c
\end{eqnarray}
となります。
上記の式を方眼グラフで描くと、直線となります。
また、両対数グラフにプロットするということは、方眼グラフでは\({\log}_{10}y\)を縦軸に、\({\log}_{10}x\)を横軸にとることと等しいため、両対数グラフの場合は以下の式となります。
\begin{eqnarray}
y&=&ax+c
\end{eqnarray}
上式は直線の式となることが分かります。
ここで、べき関数\((y=cx^a)\)は両対数グラフでは直線\((y=ax+c)\)になるため、
べき関数\((y=cx^a)\)のべき\(a\)は直線\((y=ax+c)\)の傾き\(a\)と等しくなることが分かります。また、べき関数\((y=cx^a)\)の\(c\)は両対数グラフにおける切片\(c\)と等しくなることも分かります。
また、直線\((y=ax+c\)の2点\((x_1,y_1)\),\((x_2,y_2)\)を結んだ時の傾きaは
\begin{eqnarray}
a=\frac{{\log}_{10}y_2-{\log}_{10}y_1}{{\log}_{10}x_2-{\log}_{10}x_1}
\end{eqnarray}
となります。
まとめ
この記事では『片対数グラフ』と『両対数グラフ』について、以下の内容を説明しました。
当記事のまとめ
- 指数関数\((y=ca^x)\)は片対数グラフでは直線\((y=Ax+c)\)になる
- 指数関数\((y=ca^x)\)の底\(a\)は\(a=10^A\)で求めることができる
- 指数関数\((y=ca^x)\)の\(c\)は片対数グラフにおける切片\(c\)と等しくなる
- べき関数\((y=cx^a)\)は両対数グラフでは直線\((y=ax+c)\)になる
- べき関数\((y=cx^a)\)のべき\(a\)は直線\((y=ax+c)\)の傾き\(a\)と等しくなる
- べき関数\((y=cx^a)\)の\(c\)は両対数グラフにおける切片\(c\)と等しくなる
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






