【ソレノイドコイルの自己インダクタンス】『公式』と『導出方法』について！

この記事ではソレノイドコイルの自己インダクタンスについて

『無限長ソレノイドコイル』の自己インダクタンスの公式
『有限長ソレノイドコイル』の自己インダクタンスの公式
『無限長ソレノイドコイル』の自己インダクタンスの問題

などを図を用いて分かりやすく説明しています。

『ソレノイドコイル』の自己インダクタンス

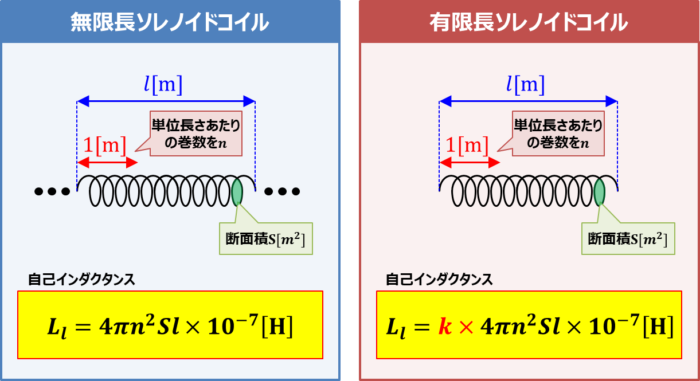
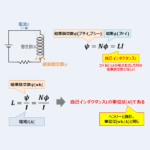
ソレノイドコイル(導線をグルグルと円筒状に巻いたコイル)の長さ\(l{\mathrm{[m]}}\)における自己インダクタンス\(L_l{\mathrm{[H]}}\)は次式で表されます。

『ソレノイドコイル』の自己インダクタンス

無限長ソレノイドコイルの場合

\begin{eqnarray}
L_l=4{\pi}n^2Sl×10^{-7}{\mathrm{[H]}}
\end{eqnarray}

有限長ソレノイドコイルの場合

\begin{eqnarray}
L_l=k×4{\pi}n^2Sl×10^{-7}{\mathrm{[H]}}
\end{eqnarray}
\(n\)：単位長さあたりの巻数
\(S\)：断面積\({\mathrm{[m^2]}}\)
\(l\)：長さ\({\mathrm{[m]}}\)
\(k\)：長岡係数

この記事では上式の導出方法について説明します。

『無限長ソレノイドコイル』の自己インダクタンス

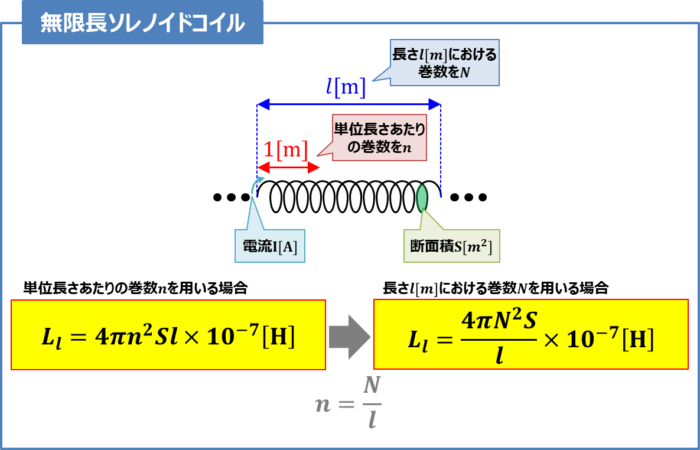
単位長さあたり(\(1{\mathrm{[m]}}\)あたり)の巻数が\(n\)、断面積が\(S{\mathrm{[m^2]}}\)の無限長ソレノイドコイルに電流\(I{\mathrm{[A]}}\)が流れている時、ソレノイド内部の磁界\(H{\mathrm{[A/m]}}\)は次式となります。

\begin{eqnarray}
H=nI{\mathrm{[A/m]}}\tag{1}
\end{eqnarray}

そのため、磁束密度\(B{\mathrm{[T]}}\)は真空の透磁率\({\mu}_0=4{\pi}×10^{-7}\)を用いると、次式となります。

\begin{eqnarray}
B={\mu}_0H={\mu}_0nI{\mathrm{[T]}}\tag{2}
\end{eqnarray}

ソレノイドの断面\(S\)と交わる磁束\({\phi}{\mathrm{[wb]}}\)は次式となります。

\begin{eqnarray}
{\phi}=BS={\mu}_0nIS{\mathrm{[wb]}}\tag{3}
\end{eqnarray}

したがって、長さ\(1{\mathrm{[m]}}\)あたりの磁束鎖交数\({\psi}{\mathrm{[wb]}}\)は次式となります。

\begin{eqnarray}
{\psi}=n{\phi}={\mu}_0n^2IS{\mathrm{[wb]}}\tag{4}
\end{eqnarray}

磁束鎖交数\({\psi}\)と自己インダクタンス\(L\)の関係は『\({\psi}＝LI\)』なので、長さ\(1{\mathrm{[m]}}\)あたりの自己インダクタンス\(L\)は次式となります。

\begin{eqnarray}
L=\frac{{\psi}}{I}=\frac{{\mu}_0n^2IS}{I}={\mu}_0n^2S=4{\pi}n^2S×10^{-7}{\mathrm{[H/m]}}\tag{5}
\end{eqnarray}

したがって、長さ\(l{\mathrm{[m]}}\)における自己インダクタンス\(L_l\)は次式となります。

\begin{eqnarray}
L_l=L×l={\mu}_0n^2Sl=4{\pi}n^2Sl×10^{-7}{\mathrm{[H]}}\tag{6}
\end{eqnarray}

補足

長さ\(l{\mathrm{[m]}}\)における巻数を\(N\)とすると、『長さ\(l{\mathrm{[m]}}\)における巻数\(N\)』と『長さ\(1{\mathrm{[m]}}\)あたりの巻数\(n\)』は次式の関係があります。

\begin{eqnarray}
N&=&nl\\
{\Leftrightarrow}n&=&\frac{N}{l}\tag{7}
\end{eqnarray}

(7)式を(6)式に代入すると、次式となります。

\begin{eqnarray}
L_l&=&{\mu}_0n^2Sl\\
&=&{\mu}_0\left(\frac{N}{l}\right)^2Sl\\
&=&\frac{{\mu}_0N^2S}{l}\\
&=&\frac{4{\pi}N^2S}{l}×10^{-7}{\mathrm{[H]}}\tag{8}
\end{eqnarray}

上式も参考書やネットで見かけることがあります。

『有限長ソレノイドコイル』の自己インダクタンス

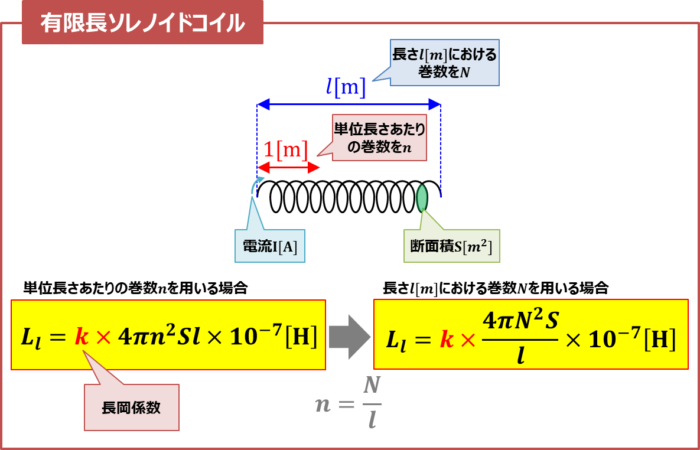
有限長ソレノイドの場合、長さ\(l{\mathrm{[m]}}\)における自己インダクタンス\(L_l\)は次式となります。

\begin{eqnarray}
L_l=k×{\mu}_0n^2Sl=k×4{\pi}n^2Sl×10^{-7}{\mathrm{[H]}}\tag{9}
\end{eqnarray}

上式において、\(k\)は長岡係数と呼ばれるものです。長岡係数は『無限長ソレノイドコイルの自己インダクタンスを求める公式((6)式)』から、有限長ソレノイドのインダクタンスを求められるようにした係数です。長岡半太郎によって提唱されました。ソレノイドの「直径/長さ」の値によって長岡係数\(k\)が決まります。「直径/長さ」が0の場合、『\(k=1\)』であり、「直径/長さ」が大きくなると、長岡係数\(k\)が小さくなります。『\(k=1\)』の場合、『無限長ソレノイドコイルの自己インダクタンスを求める公式((6)式)』と等しくなります。

補足

長さ\(l{\mathrm{[m]}}\)における巻数を\(N\)の式に変形します。(7)式を(9)式に代入すると、次式となります。

\begin{eqnarray}
L_l&=&k×{\mu}_0n^2Sl\\
&=&k×{\mu}_0\left(\frac{N}{l}\right)^2Sl\\
&=&k×\frac{{\mu}_0N^2S}{l}\\
&=&k×\frac{4{\pi}N^2S}{l}×10^{-7}{\mathrm{[H]}}\tag{10}
\end{eqnarray}

上式も参考書やネットで見かけることがあります。

『無限長ソレノイドコイル』の自己インダクタンスに関する問題

問題文

単位長さあたりの巻数が\(2000\)回、半径\(r=3{\mathrm{[cm]}}\)の円形断面、長さ\(l=1{\mathrm{[m]}}\)の無限に長いソレノイドコイルの自己インダクタンス\(L_l\)を求めてみましょう。

回答

ソレノイドの断面積\(S{\mathrm{[m^2]}}\)は次式となります。

\begin{eqnarray}
S&=&{\pi}r^2\\
&=&{\pi}×(3.0×10^{-2})^2\\
&{\;}{\approx}{\;}&0.0028{\mathrm{[m^2]}}
\end{eqnarray}

したがって、自己インダクタンス\(L_l\)は次式となります。

\begin{eqnarray}
L_l&=&4{\pi}n^2Sl×10^{-7}\\
&{\;}{\approx}{\;}&4{\pi}×2000^2×0.0028×1×10^{-7}\\
&{\;}{\approx}{\;}&1.4×10^{-2}{\mathrm{[H]}}
\end{eqnarray}