この記事では『サレンキー型ローパスフィルタ』について
- サレンキー型ローパスフィルタとは
- サレンキー型ローパスフィルタの『伝達関数』,『カットオフ周波数』,『Q値』
- サレンキー型ローパスフィルタの『周波数特性』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
サレンキー型ローパスフィルタ
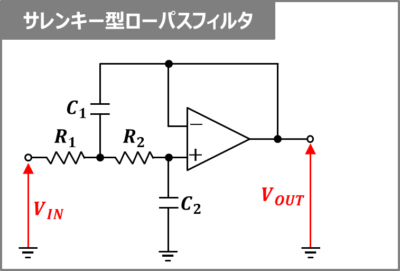
上図にサレンキー型ローパスフィルタの回路構成を示しています。
サレンキー型ローパスフィルタは、オペアンプと抵抗\(R_1,R_2\)とコンデンサ\(C_1,C_2\)で構成されている2次ローパスフィルタです。入力電圧\(V_{IN}\)の低周波成分を通過させ、高周波成分を遮断します。
後ほど導出方法など詳細に説明しますが、サレンキー型ローパスフィルタの『伝達関数』,『カットオフ周波数』,『Q値』の式と『周波数特性』をまとめると、下記のようになります。
サレンキー型ローパスフィルタのまとめ
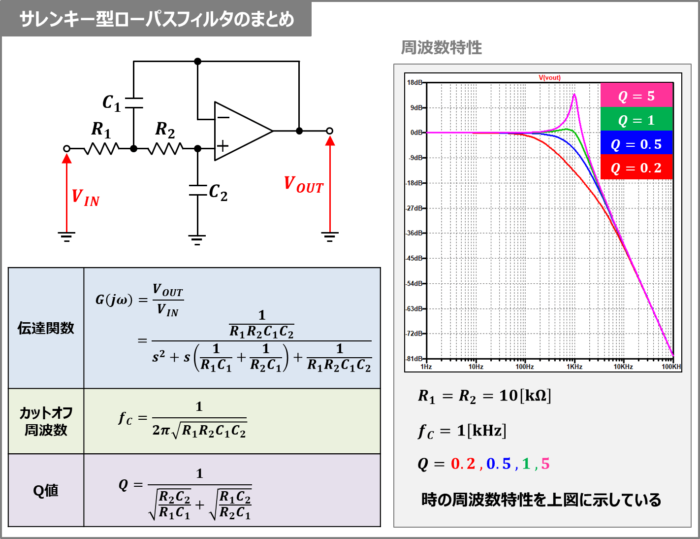
- 伝達関数\(G(j{\omega})\)
- カットオフ周波数\(f_C\)
- Q値
\begin{eqnarray}
G(j{\omega})=\frac{V_{OUT}}{V_{IN}}=\frac{\displaystyle\frac{1}{R_1R_2C_1C_2}}{s^2+s\left(\displaystyle\frac{1}{R_1C_1}+\displaystyle\frac{1}{R_2C_1}\right)+\displaystyle\frac{1}{R_1R_2C_1C_2}}
\end{eqnarray}
\begin{eqnarray}
f_C=\frac{1}{2{\pi}\sqrt{R_1R_2C_1C_2}}
\end{eqnarray}
\begin{eqnarray}
Q=\frac{1}{\sqrt{\displaystyle\frac{R_2C_2}{R_1C_1}}+\sqrt{\displaystyle\frac{R_1C_2}{R_2C_1}}}
\end{eqnarray}
あわせて読みたい
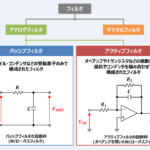
この記事で説明している『サレンキー型ローパスフィルタ』のように、オペアンプなどの能動素子に抵抗やコンデンサを組み合わせて構成されたフィルタのことを『アクティブフィルタ』といいます。
一方、抵抗・コイル・コンデンサなどの受動素子のみで構成されたフィルタのことを『パッシブフィルタ』といいます。
『アクティブフィルタ』と『パッシブフィルタ』の特徴については下記の記事でまとめていますので、ご参考になると幸いです。
-

『パッシブフィルタ』と『アクティブフィルタ』の違いについて!
続きを見る
サレンキー型ローパスフィルタの伝達関数
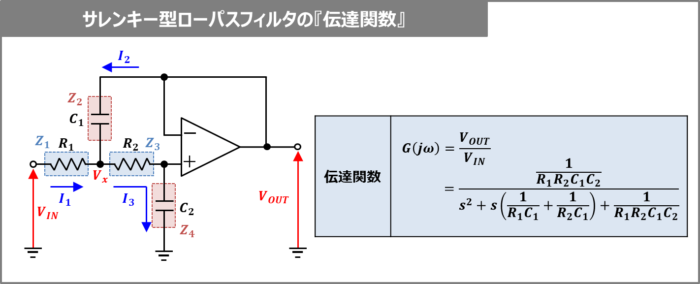

上図に示すように、抵抗\(R_1\)に流れる電流を\(I_1\)、コンデンサ\(C_1\)に流れる電流を\(I_2\)、抵抗\(R_2\)とコンデンサ\(C_2\)に流れる電流を\(I_3\)と置き、抵抗\(R_1\)と抵抗\(R_2\)の接続点の電圧を電圧\(V_x\)とし、抵抗\(R_1\)のインピーダンス、コンデンサ\(C_1\)のインピーダンス、抵抗\(R_2\)のインピーダンス、コンデンサ\(C_2\)のインピーダンスをそれぞれ\(Z_1,Z_2,Z_3,Z_4\)とすると、次式が成り立ちます。
\begin{eqnarray}
I_1&=&\frac{V_{IN}-V_x}{Z_1}\tag{1}\\
\\
I_2&=&\frac{V_{OUT}-V_x}{Z_2}\tag{2}\\
\\
I_3&=&\frac{V_x}{Z_3+Z_4}\tag{3}\\
\\
I_3&=&\frac{V_{OUT}}{Z_4}\tag{4}\\
\\
I_3&=&I_1+I_2\tag{5}
\end{eqnarray}
(3)式と(4)式を用いると、電圧\(V_x\)は次式で表すことができます。
\begin{eqnarray}
&&\frac{V_x}{Z_3+Z_4}=\frac{V_{OUT}}{Z_4}\\
\\
{\Leftrightarrow}&&V_x=\frac{Z_3+Z_4}{Z_4}V_{OUT}\tag{6}
\end{eqnarray}
(6)式を(1)式と(2)式に代入すると、電流\(I_1\)と\(I_2\)は次式で表すことができます。
\begin{eqnarray}
I_1&=&\frac{V_{IN}-\displaystyle\frac{Z_3+Z_4}{Z_4}V_{OUT}}{Z_1}=\frac{Z_4V_{IN}-(Z_3+Z_4)V_{OUT}}{Z_1Z_4}\tag{7}\\
\\
I_2&=&\frac{V_{OUT}-\displaystyle\frac{Z_3+Z_4}{Z_4}V_{OUT}}{Z_2}=\frac{Z_4V_{OUT}-(Z_3+Z_4)V_{OUT}}{Z_2Z_4}=-\frac{Z_3}{Z_2Z_4}V_{OUT}\tag{8}
\end{eqnarray}
(4)式,(7)式,(8)式を(5)式に代入すると、次式となります。
\begin{eqnarray}
\frac{V_{OUT}}{Z_4}=\frac{Z_4V_{IN}-(Z_3+Z_4)V_{OUT}}{Z_1Z_4}-\frac{Z_3}{Z_2Z_4}V_{OUT}\tag{9}
\end{eqnarray}
(9)式の両辺に『\(Z_1Z_2Z_4\)』を掛けると、電圧\(V_{OUT}\)は次式で表すことができます。
\begin{eqnarray}
Z_1Z_2V_{OUT}&=&Z_2Z_4V_{IN}-Z_2(Z_3+Z_4)V_{OUT}-Z_1Z_3V_{OUT}\\
\\
&=&Z_2Z_4V_{IN}-Z_2Z_3V_{OUT}-Z_2Z_4V_{OUT}-Z_1Z_3V_{OUT}\\
\\
{\Leftrightarrow}(Z_1Z_3+Z_1Z_2+Z_2Z_3+Z_2Z_4)V_{OUT}&=&Z_2Z_4V_{IN}\\
\\
{\Leftrightarrow}V_{OUT}&=&\frac{Z_2Z_4}{Z_1Z_3+Z_1Z_2+Z_2Z_3+Z_2Z_4}V_{IN}\\
\\
&=&\frac{1}{\displaystyle\frac{Z_1Z_3}{Z_2Z_4}+\displaystyle\frac{Z_1+Z_3}{Z_4}+1}V_{IN}\tag{10}
\end{eqnarray}
ここで、インピーダンス\(Z_1~Z_4\)は次式で表されます。
\begin{eqnarray}
Z_1&=&R_1\\
\\
Z_2&=&\frac{1}{j{\omega}C_1}=\frac{1}{sC_1}\\
\\
Z_3&=&R_2\\
\\
Z_4&=&\frac{1}{j{\omega}C_2}=\frac{1}{sC_2}\\
\end{eqnarray}
上記のインピーダンスを(10)式に代入すると、電圧\(V_{OUT}\)は次式で表すことができます。
\begin{eqnarray}
V_{OUT}&=&\frac{1}{\displaystyle\frac{R_1R_2}{\displaystyle\frac{1}{sC_1}{\;}{\cdot}{\;}\displaystyle\frac{1}{sC_2}}+\displaystyle\frac{R_1+R_2}{\displaystyle\frac{1}{sC_2}}+1}V_{IN}\\
\\
&=&\frac{1}{s^2R_1R_2C_1C_2+sC_2(R_1+R_2)+1}V_{IN}\\
\\
&=&\frac{\displaystyle\frac{1}{R_1R_2C_1C_2}}{s^2+s\left(\displaystyle\frac{1}{R_1C_1}+\displaystyle\frac{1}{R_2C_1}\right)+\displaystyle\frac{1}{R_1R_2C_1C_2}}V_{IN}\tag{11}\\
\end{eqnarray}
伝達関数\(G(j{\omega})\)は入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の比です。そのため、(11)式を変形すると、伝達関数\(G(j{\omega})\)は次式で表すことができます。
G(j{\omega})=\frac{V_{OUT}}{V_{IN}}=\frac{\displaystyle\frac{1}{R_1R_2C_1C_2}}{s^2+s\left(\displaystyle\frac{1}{R_1C_1}+\displaystyle\frac{1}{R_2C_1}\right)+\displaystyle\frac{1}{R_1R_2C_1C_2}}\tag{12}
\end{eqnarray}
サレンキー型ローパスフィルタのカットオフ周波数とQ値
2次系の伝達関数は次式で表されます。
\begin{eqnarray}
G(j{\omega})=\frac{{{\omega}_n}^2}{s^2+2{\zeta}{\omega}_ns+{{\omega}_n}^2}\tag{13}
\end{eqnarray}
上式において\({\omega}_n\)は固有角周波数[rad/s]、\({\zeta}\)は減衰係数となります。
また、共振の鋭さ\(Q\)と減衰係数\({\zeta}\)には『\({\zeta}=\displaystyle\frac{1}{2Q}\)』の関係があるので、(13)式は次式に変形することができます。
\begin{eqnarray}
G(j{\omega})=\frac{{{\omega}_n}^2}{s^2+\displaystyle\frac{{\omega}_n}{Q}s+{{\omega}_n}^2}\tag{14}
\end{eqnarray}
(11)式と(14)式より、固有角周波数\({\omega}_n\)は次式で表されることが分かります。
\begin{eqnarray}
{\omega}_n=\frac{1}{\sqrt{R_1R_2C_1C_2}}\tag{15}
\end{eqnarray}
上式で表される固有角周波数\({\omega}_n\)はサレンキー型ローパスフィルタのカットオフ角周波数\({\omega}_C\)となります。したがって、サレンキー型ローパスフィルタのカットオフ周波数\(f_C\)は次式となります。
{\omega}_n={\omega}_C&=&\frac{1}{\sqrt{R_1R_2C_1C_2}}\\
\\
{\Leftrightarrow}f_C&=&\frac{1}{2{\pi}\sqrt{R_1R_2C_1C_2}}\tag{16}
\end{eqnarray}
また、(11)式と(14)式と(15)式を用いると、サレンキー型ローパスフィルタのQ値は次式で表されることが分かります。
\begin{eqnarray}
\frac{{\omega}_n}{Q}&=&\frac{1}{R_1C_1}+\frac{1}{R_2C_1}\\
\\
{\Leftrightarrow}Q&=&\frac{{\omega}_n}{\displaystyle\frac{1}{R_1C_1}+\displaystyle\frac{1}{R_2C_1}}\\
\\
&=&\frac{\displaystyle\frac{1}{\sqrt{R_1R_2C_1C_2}}}{\displaystyle\frac{1}{R_1C_1}+\displaystyle\frac{1}{R_2C_1}}\\
\\
&=&\frac{1}{\sqrt{\displaystyle\frac{R_2C_2}{R_1C_1}}+\sqrt{\displaystyle\frac{R_1C_2}{R_2C_1}}}\tag{17}
\end{eqnarray}
サレンキー型ローパスフィルタの設計
設計を簡単にするために、この記事では抵抗\(R_1\)と抵抗\(R_2\)は等しい抵抗値\(R\)を用いて設計します(\(R_1=R_2=R\))。
『\(R_1=R_2=R\)』とすると、(16)式は次式で表すことができます。
\begin{eqnarray}
{\omega}_C=\frac{1}{\sqrt{R_1R_2C_1C_2}}=\frac{1}{R\sqrt{C_1C_2}}\tag{18}
\end{eqnarray}
また、(17)式は以下に示すように変形することができるようになります。
\begin{eqnarray}
Q&=&\frac{1}{\sqrt{\displaystyle\frac{R_2C_2}{R_1C_1}}+\sqrt{\displaystyle\frac{R_1C_2}{R_2C_1}}}\\
\\
&=&\frac{1}{\sqrt{\displaystyle\frac{RC_2}{RC_1}}+\sqrt{\displaystyle\frac{RC_2}{RC_1}}}\\
\\
&=&\frac{1}{2\sqrt{\displaystyle\frac{C_2}{C_1}}}\\
\\
&=&\frac{1}{2}\sqrt{\displaystyle\frac{C_1}{C_2}}\tag{19}\\
\\
{\Leftrightarrow}\sqrt{C_2}&=&\frac{\sqrt{C_1}}{2Q}\tag{20}\\
\\
{\Leftrightarrow}\sqrt{C_1}&=&2Q\sqrt{C_2}\tag{21}\\
\end{eqnarray}
ここで、(20)式を(18)式に代入すると、コンデンサ\(C_1\)は次式で表されます。
\begin{eqnarray}
{\omega}_C&=&\frac{1}{R\sqrt{C_1}×\displaystyle\frac{\sqrt{C_1}}{2Q}}\\
\\
{\Leftrightarrow}C_1&=&\frac{2Q}{{\omega}_CR}\tag{22}
\end{eqnarray}
同様に、(21)式を(18)式に代入すると、コンデンサ\(C_2\)は次式で表されます。
\begin{eqnarray}
{\omega}_C&=&\frac{1}{R×2Q\sqrt{C_2}×\sqrt{C_2}}\\
\\
{\Leftrightarrow}C_2&=&\frac{1}{2Q{\omega}_CR}\tag{23}
\end{eqnarray}
ここで、『\({\omega}_C=\displaystyle\frac{1}{C_fR}\)』と置くと、コンデンサ\(C_1\)とコンデンサ\(C_2\)は次式で表すことができます。
\begin{eqnarray}
C_1&=&2QC_f\tag{24}\\
\\
C_2&=&\frac{C_f}{2Q}\tag{25}
\end{eqnarray}
以上をまとめると、『\(R_1=R_2=R\)』とすれば、
C_1&=&\frac{2Q}{{\omega}_CR}=\frac{2Q}{2{\pi}f_C×R}=2QC_f\\
\\
C_2&=&\frac{1}{2Q{\omega}_CR}=\frac{1}{2Q×2{\pi}f_C×R}=\frac{C_f}{2Q}
\end{eqnarray}
となり、抵抗\(R\)とカットオフ周波数\(f_C\)とQ値を設定すれば、コンデンサ\(C_1\)とコンデンサ\(C_2\)の値を求めることができます。
サレンキー型ローパスフィルタの周波数特性
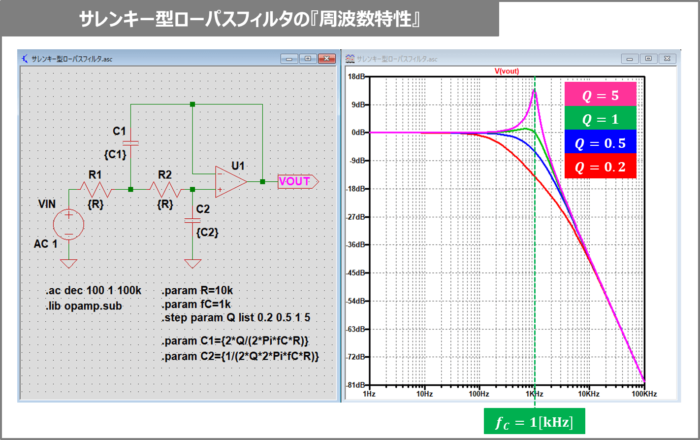

『\(R_1=R_2=R=10{\mathrm{[k{\Omega}]}}\)』、『\(f_C=1{\mathrm{[kHz]}}\)』において、Q値を0.2,0.5,1,5に変化させた時の周波数特性をLTspiceで確認します。
『周波数特性』をLTspiceで描くためには『.ac解析』を用います。
VOUT端子の電圧をプロットすることで、周波数特性を出力することができるようになります。
ローパスフィルタなので、カットオフ周波数\(f_C\)より高い周波数ではゲインが減少していることが確認できます。
『.ac dec 100 10 10k』は『信号源(ここでは入力電圧\(V_{IN}\))の周波数を10Hz~10kHzに変化させる。この時、1ディケード(10倍)当たりのステップ数を100とする。』という意味です。
LTspiceでのAC解析の方法は下記の記事で説明していますので、ご参考にしてください。
-



【LTspice】周波数特性を観測する『.ac解析』の使い方と応用
続きを見る
また、LTspiceの『.stepコマンド』については下記の記事で説明していますので、ご参考にしてください。
-


【LTspice】.stepコマンドとは
続きを見る
まとめ
この記事では『サレンキー型ローパスフィルタ』について、以下の内容を説明しました。
- サレンキー型ローパスフィルタとは
- サレンキー型ローパスフィルタの『伝達関数』,『カットオフ周波数』,『Q値』
- サレンキー型ローパスフィルタの『周波数特性』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。