RLC並列回路の電力【有効電力・無効電力・皮相電力】

この記事では『RLC並列回路の電力(有効電力・無効電力・皮相電力)』について

• RLC並列回路の電力(有効電力・無効電力・皮相電力)の計算方法

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

RLC並列回路の有効電力・無効電力・皮相電力

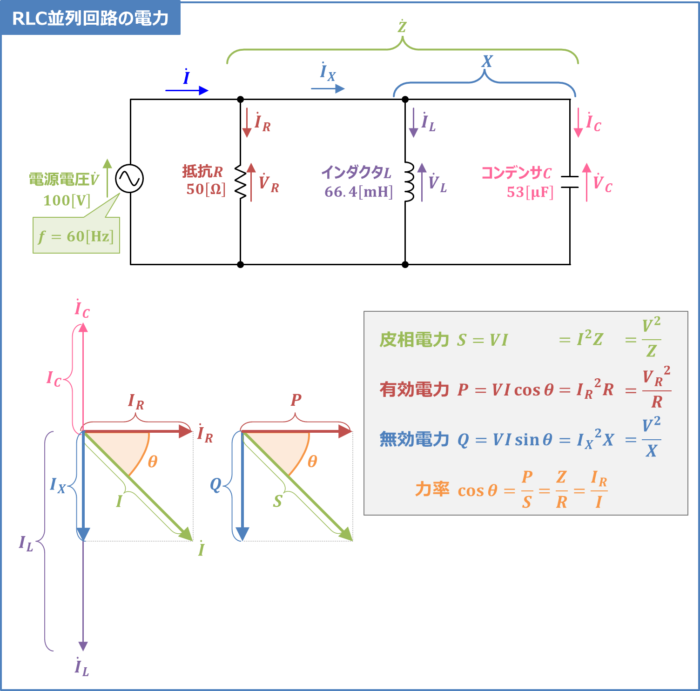
上図に示しているのは抵抗\(R\)とインダクタ\(L\)とコンデンサ\(C\)を並列に接続したRLC並列回路です。一例としてRLC並列回路のパラメータは下記としています。

• 電源電圧：\({\dot{V}}=100{\;}{\mathrm{[V]}}\)
• 電源電圧\({\dot{V}}\)の周波数：\(f=60{\;}{\mathrm{[Hz]}}\)
• 抵抗\(R\)の抵抗値：\(R=50{\;}{\mathrm{[{\Omega}]}}\)
• インダクタ\(L\)のインダクタンス：\(L=66.4{\;}{\mathrm{[mH]}}\)
• コンデンサ\(C\)のキャパシタンス：\(C=53{\;}{\mathrm{[μF]}}\)

このRLC並列回路の有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)は下記の手順(ステップ1～4)で求めることができます。

では、これから各手順について順番に説明します。上図に示している「図1：RLC並列回路の有効電力・無効電力・皮相電力」を見ながらこの記事を読むと理解しやすくなると思います。

RLC並列回路のインピーダンスの大きさを求める

「抵抗\(R\)のインピーダンス\({\dot{Z}}_R\)」と「インダクタ\(L\)のインピーダンス\({\dot{Z}}_L\)」と「コンデンサ\(C\)のインピーダンス\({\dot{Z}}_C\)」はそれぞれ次式で表されます。

\begin{eqnarray}
{\dot{Z}_R}&=&R\tag{1}\\
\\
{\dot{Z}_L}&=&jX_L=j{\omega}L\tag{2}\\
\\
{\dot{Z}_C}&=&-jX_C=-j\frac{1}{{\omega}C}\tag{3}
\end{eqnarray}

上式において、\(X_L\)は誘導性リアクタンス(インダクタ\(L\)の抵抗成分)、\(X_C\)は容量性リアクタンス(コンデンサ\(C\)の抵抗成分)と呼ばれています。また、\({\omega}\)は角周波数(角速度とも呼ばれる)であり、\({\omega}=2{\pi}f\)の関係があります。

ここで、誘導性リアクタンス\(X_L\)と容量性リアクタンス\(X_C\)は次式で求めることができます。

\begin{eqnarray}
X_L&=&{\omega}L=2{\pi}fL=2{\pi}{\;}{\cdot}{\;}60{\;}{\cdot}{\;}66.4×10^{-3}{\;}{\approx}{\;}25{\;}{\mathrm{[{\Omega}]}}\tag{4}\\
\\
X_C&=&\frac{1}{{\omega}C}=\frac{1}{2{\pi}fC}=\frac{1}{2{\pi}{\;}{\cdot}{\;}60{\;}{\cdot}{\;}53×10^{-6}}{\;}{\approx}{\;}50{\;}{\mathrm{[{\Omega}]}}\tag{5}
\end{eqnarray}

ここで、インダクタ\(L\)とコンデンサ\(C\)の合成リアクタンス\(X\)は次式で求めることができます。

\begin{eqnarray}
X&=&\left|\frac{1}{\displaystyle\frac{1}{X_L}-\displaystyle\frac{1}{X_C}}\right|=\left|\frac{1}{\displaystyle\frac{1}{25}-\displaystyle\frac{1}{50}}\right|=50{\;}{\mathrm{[{\Omega}]}}\tag{6}
\end{eqnarray}

『それぞれのインピーダンスの逆数の和』が『RLC並列回路のインピーダンス\({\dot{Z}}\)の逆数』となるため、次式が成り立ちます。

\begin{eqnarray}
\frac{1}{{\dot{Z}}}&=&\frac{1}{{\dot{Z}_R}}+\frac{1}{{\dot{Z}_L}}+\frac{1}{{\dot{Z}_C}}\\
\\
&=&\frac{1}{R}+\frac{1}{jX_L}+\frac{1}{-jX_C}\\
\\
&=&\frac{1}{R}-j\frac{1}{X_L}+j\frac{1}{X_C}\\
\\
&=&\frac{1}{R}+j\left(\frac{1}{X_C}-\frac{1}{X_L}\right)\tag{7}
\end{eqnarray}

上式の分母と分子をひっくり返すと次式となります。

\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{{\dot{Z}_R}}+\displaystyle\frac{1}{{\dot{Z}_L}}+\displaystyle\frac{1}{{\dot{Z}_C}}}\\
\\
&=&\frac{1}{\displaystyle\frac{1}{R}+j\left(\frac{1}{X_C}-\frac{1}{X_L}\right)}\tag{8}
\end{eqnarray}

RLC並列回路のインピーダンスの大きさ\(Z\)は(8)式で示した「\({\dot{Z}}=\displaystyle\frac{1}{\displaystyle\frac{1}{R}+j\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)}\)」の絶対値であるため、次式で求めることができます。

\begin{eqnarray}
Z=|{\dot{Z}}|&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{X_C}-\displaystyle\frac{1}{X_L}\right)^2}}\\
\\
&=&\frac{1}{\sqrt{\left(\displaystyle\frac{1}{50}\right)^2+\left(\displaystyle\frac{1}{50}-\displaystyle\frac{1}{25}\right)^2}}\\
\\
&=&25\sqrt{2}{\;}{\mathrm{[{\Omega}]}}\tag{9}
\end{eqnarray}

RLC並列回路に流れる電流の大きさを求める

電源電圧の大きさ\(V\)は以下の値となります。

\begin{eqnarray}
V=|{\dot{V}}|=|100|=100{\;}{\mathrm{[V]}}\tag{10}
\end{eqnarray}

(9)式と(10)式より、RLC並列回路に流れる電流の大きさ\(I\)は次式で求めることができます。

\begin{eqnarray}
I=\frac{V}{Z}=\frac{100}{25\sqrt{2}}=2\sqrt{2}{\;}{\mathrm{[A]}}\tag{11}
\end{eqnarray}

並列回路なので「抵抗\(R\)にかかる電圧の大きさ\(V_R\)」と「インダクタ\(L\)にかかる電圧の大きさ\(V_L\)」と「コンデンサ\(C\)にかかる電圧の大きさ\(V_C\)」は「電源電圧の大きさ\(V\)」と等しくなり、次式が成り立ちます。

\begin{eqnarray}
V=V_R=V_L=V_C=100{\;}{\mathrm{[V]}}\tag{12}
\end{eqnarray}

そのため、「抵抗\(R\)に流れる電流の大きさ\(I_R\)」と「インダクタ\(L\)に流れる電流の大きさ\(I_L\)」と「コンデンサ\(C\)に流れる電流の大きさ\(I_C\)」は次式で求めることができます。

\begin{eqnarray}
I_R&=&\frac{V_R}{R}=\frac{100}{50}=2{\;}{\mathrm{[A]}}\tag{13}\\
\\
I_L&=&\frac{V_L}{X_L}=\frac{100}{25}=4{\;}{\mathrm{[A]}}\tag{14}\\
\\
I_C&=&\frac{V_C}{X_C}=\frac{100}{50}=2{\;}{\mathrm{[A]}}\tag{15}
\end{eqnarray}

また、合成リアクタンス\(X\)に流れる電流の大きさ\(I_X\)は次式で求めることができます。

\begin{eqnarray}
I_X=\frac{V}{X}=\frac{100}{50}=2{\;}{\mathrm{[A]}}\tag{16}
\end{eqnarray}

(16)式から分かるように、合成リアクタンス\(X\)に流れる電流の大きさ\(I_X\)は「インダクタ\(L\)に流れる電流の大きさ\(I_L\)」と「コンデンサ\(C\)に流れる電流の大きさ\(I_C\)」の差(\(|I_L-I_C|\))になります。

RLC並列回路の力率\({\cos}{\theta}\)を求める

RLC並列回路の力率\({\cos}{\theta}\)は「抵抗\(R\)」における「インピーダンスの大きさ\(Z\)」の比率であり、次式で求めることができます。

\begin{eqnarray}
{\cos}{\theta}=\frac{Z}{R}=\frac{25\sqrt{2}}{50}=\frac{1}{\sqrt{2}}\tag{17}
\end{eqnarray}

RLC並列回路の有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)を求める

「電源電圧の大きさ\(V\)」、「RLC並列回路に流れる電流の大きさ\(I\)」、「RLC並列回路の力率\({\cos}{\theta}\)」を求めれば、有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)を計算することができます。

【RLC並列回路】皮相電力\(S\)の求め方

まず、皮相電力\(S\)から求めてみましょう。皮相電力\(S\)は次式で求めることができます。

\begin{eqnarray}
S=VI=100{\;}{\cdot}{\;}2\sqrt{2}=200\sqrt{2}{\;}{\mathrm{[VA]}}\tag{19}
\end{eqnarray}

【RLC並列回路】有効電力\(P\)の求め方

では次に、有効電力\(P\)を求めてみましょう。有効電力\(P\)は次式で求めることができます。

\begin{eqnarray}
P=VI{\cos}{\theta}=100{\;}{\cdot}{\;}2\sqrt{2}{\;}{\cdot}{\;}\frac{1}{\sqrt{2}}=200{\;}{\mathrm{[W]}}\tag{22}
\end{eqnarray}

【RLC並列回路】無効電力\(Q\)の求め方

最後に、無効電力\(Q\)を求めてみましょう。無効電力\(Q\)は次式で求めることができます。

\begin{eqnarray}
Q=VI{\sin}{\theta}=VI\sqrt{1-{\cos}^2{\theta}}=100{\;}{\cdot}{\;}2\sqrt{2}{\;}{\cdot}{\;}\sqrt{1-\left(\frac{1}{\sqrt{2}}\right)^2}=200{\;}{\mathrm{[var]}}\tag{25}
\end{eqnarray}

なお、RLC並列回路の力率\({\cos}{\theta}\)は「皮相電力\(S\)」における「有効電力\(P\)」の比率でも求めることができます。計算すると、次式のようになり、(17)式や(18)式と等しくなることが分かります。

\begin{eqnarray}
{\cos}{\theta}=\frac{P}{S}=\frac{200}{200\sqrt{2}}=\frac{1}{\sqrt{2}}\tag{28}
\end{eqnarray}

まとめ

この記事では『RLC並列回路の電力(有効電力・無効電力・皮相電力)』について、以下の内容を説明しました。

• RLC並列回路の電力(有効電力・無効電力・皮相電力)の計算方法

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。

全記事一覧

また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。