この記事では抵抗率について図を用いて分かりやすく説明しています。
抵抗率とは
最初に抵抗率の重要ポイントについて説明します(後ほど詳しく説明します)。
抵抗率とは
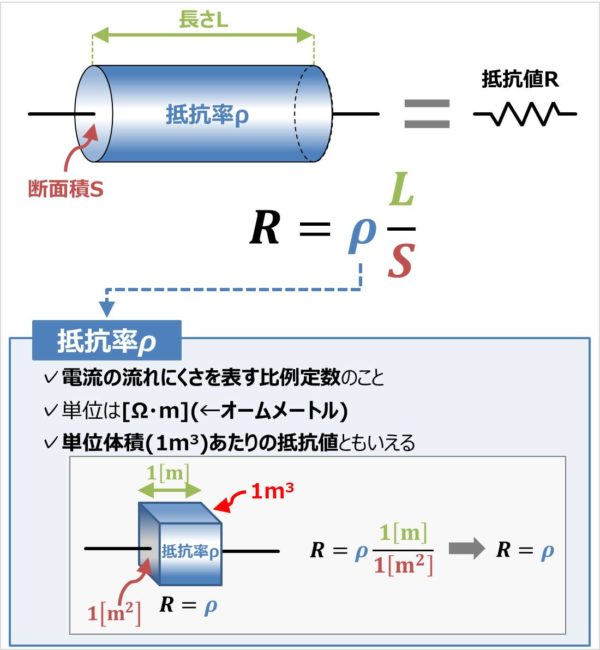
- 抵抗率は電流の流れにくさを表す比例定数です。
- 記号はギリシャ文字のρ(ロー)で表します。
- 単位は[Ω・m](←オームメートル)です。
- 抵抗率は単位体積(1m3)あたりの抵抗値ともいえます。
- 抵抗率は導体の材料によって決まる値です。
- 抵抗率は温度によって変わるという特徴があります。
では、これから上の各ポイントについて詳しく説明していきます。
導体の抵抗値Rは導体の長さLに比例し、導体の断面積Sに反比例するため、次式で表されます。
\begin{eqnarray}
R={\rho}\frac{L}{S}\tag{1}
\end{eqnarray}
上式の『L/S』の前に付いている比例定数が抵抗率ρです。上式より、抵抗率ρが大きいほど、導体の抵抗値Rが大きくなります。つまり、抵抗率とは、電流の流れにくさを表す比例定数ということになります。
また、導体の長さLを1[m]、導体の断面積Sを1[m2]とすると、(1)式は、
\begin{eqnarray}
R={\rho}\frac{L}{S}={\rho}\frac{1{\mathrm{[m]}}}{1{\mathrm{[m^2]}}}={\rho}\tag{2}
\end{eqnarray}
となるため、抵抗値Rと抵抗率ρが等しくなります。つまり、抵抗率は単位体積(1m3)あたりの導体の抵抗値ということになります。
なお、(1)式において、抵抗率ρを左辺にもっていくと、次式となります。
\begin{eqnarray}
{\rho}=R\frac{S}{L}\tag{3}
\end{eqnarray}
補足
- 抵抗率は英語では「Resistivity」と書きます。
抵抗率の値
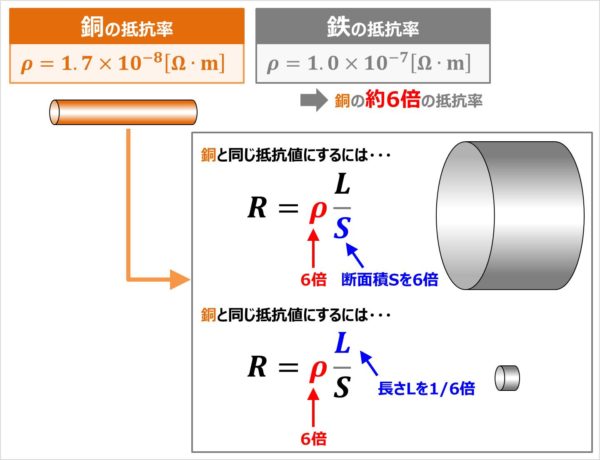
抵抗率は導体の材料によって決まる値となっています。
例えば、温度が20[℃]の場合、銅の抵抗率ρは「1.7×10-8[Ω・m]」であり、鉄の抵抗率ρは「1.0×10-7[Ω・m]」となっています。つまり、鉄は銅の約6倍の抵抗率ということになります。鉄の方が6倍電流が流れにくいということです。
銅と同じ抵抗値にするには、(1)式より、鉄の断面積Sを6倍にするか、鉄の長さLを1/6倍にする必要があるということになります。
抵抗率の単位
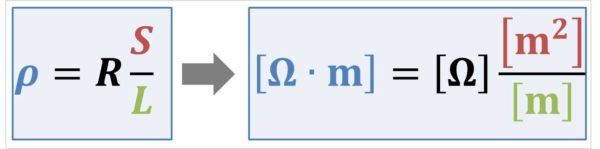
抵抗率の単位は、抵抗値Rの単位が[Ω]、導体の長さLの単位が[m]、導体の断面積Sの単位が[m2]となるため、(3)式から
\begin{eqnarray}
{\rho}=R\frac{S}{L}{\Rightarrow}{\mathrm{[Ω]}}\frac{{\mathrm{[m^2]}}}{{\mathrm{[m]}}}={\mathrm{[Ω{\cdot}m]}}\tag{4}
\end{eqnarray}
となり、単位が[Ω・m](←オームメートル)となります。
補足
- 抵抗率ρの単位は[Ω・m]の他、[Ω・cm](←オームセンチメートル)で表すこともあります。「cm」の“c”が「-2乗」を表すため、1[Ω・m]=100[Ω・cm]の関係となります。
『抵抗率』と『導電率』の違い
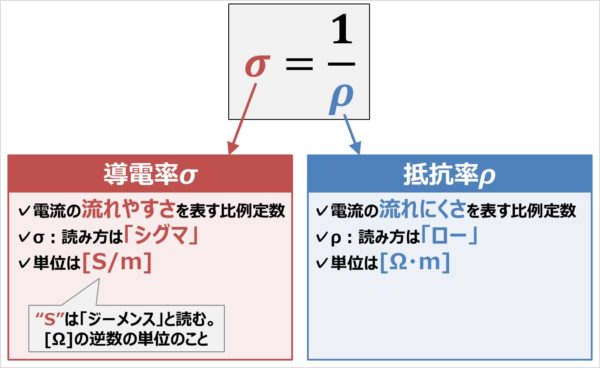
抵抗率ρ(ロー)は『電流の流れにくさを表す比例定数』です。一方、導電率σ(シグマ)は『電流の流れやすさを表す比例定数』であり、導電率σは次式のように抵抗率ρの逆数となります。
\begin{eqnarray}
{\sigma}=\frac{1}{{\rho}}\tag{5}
\end{eqnarray}
導電率σの単位は[S/m]となっています。[S/m]の中にある”S"は『ジーメンス(Siemens)』と読み、[Ω]の逆数の単位となっています。
補足
- 導電率は英語では「Conductivity」と書きます。
- 導電率は電気伝導率(Electrical Conductivity)や電気伝導度とも呼ばれています。理学系では「電気伝導率」、工学系では「導電率」と呼ばれる傾向があります。
- 『ジーメンス(Siemens)』はドイツの物理学者、ヴェルナー・フォン・ジーメンス (Werner von Siemens)が由来となっています。
抵抗率の温度特性
抵抗率ρは温度によって変化します。
温度が高いほど、抵抗率が大きくなります。これは、導体内にある自由電子は陽イオンにぶつかりながら移動しますが、温度が高くなればなるほど、陽イオンの振動が激しくなり、自由電子の移動を邪魔するからです。
温度をtとすると、温度tと抵抗率ρの関係は次式となります。
\begin{eqnarray}
{\rho}={\rho}_0(1+{\alpha}t)\tag{6}
\end{eqnarray}
上式において、
- \({\rho}\):温度がt[℃]の時の抵抗率
- \({\rho}_0\):温度が0[℃]の時の抵抗率
- \({\alpha}\):抵抗率の温度係数
となっています。温度係数αは温度が1℃上がるごとの抵抗率の変化量であり、単位は[/℃]です。
また、ここで、抵抗値Rの抵抗に電流Iが流れている時、電圧Vはオームの法則より次式となります。
\begin{eqnarray}
V=RI\tag{7}
\end{eqnarray}
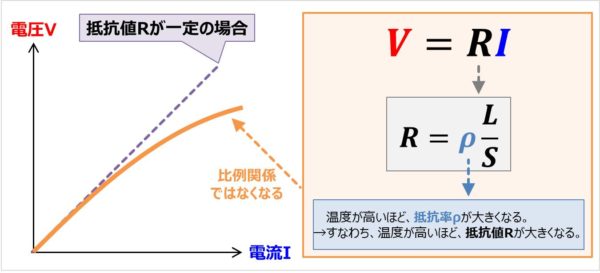
上式より抵抗値Rが一定の場合、電圧Vと電流Iは比例関係であり、上図の紫色の点線の線となります。
しかし、実際は、抵抗に電流Iが流れることによるジュール熱によって温度が上がり、抵抗率ρが大きくなります(すなわち、抵抗値Rが大きくなる)。そのため、厳密には、電圧Vと電流Iは上図のオレンジ色の線のように比例関係ではなくなります。
補足
- 温度係数αの単位ですが、(6)式より「αt」が単位を持たない数字の「1」と同じにならなければいけません。温度tの単位は[℃]なので、単位を消すために、温度係数αの単位は[/℃]となります。
- 抵抗率は温度によって変わるので、ある材料の抵抗率を示す時には、『温度が20[℃]の時における抵抗率』で示されていることが多いです。
- 電子部品の「抵抗」は1種類の導体でなく2種類以上の導体の合金で構成されている場合があります。そのため、必ずしも温度が高いほど、抵抗値が大きくなるとは限りません。
抵抗率の様々な呼び方
抵抗率は以下のように分野によって様々な呼び方が存在します。
- 電気の分野
- 物理の分野
- 電子の分野
- 材料の分野
電気抵抗率(Electrical Resistivity)と呼ぶことが多いです。
抵抗率(Resistivity)と呼ぶことが多いです。
比抵抗(Specific Electrical Resistance)と呼ぶことが多いです。
体積抵抗率(Volume Resistivity)や体積固有抵抗や固有抵抗と呼ぶことが多いです。
まとめ
この記事では抵抗率について、以下の内容を説明しました。
当記事のまとめ
- 抵抗率とは
- 抵抗率の値
- 抵抗率の単位
- 抵抗率と導電率の違い
- 抵抗率の温度特性
- 抵抗率の呼び方
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






