【リアクタンスとは】『単位』や『計算方法』などのまとめ！

リアクタンスXは「交流回路における電流の流れにくさ」を表すものです。

この記事ではこのリアクタンスについて

リアクタンスとは
リアクタンスの特徴
『誘導性リアクタンス』と『容量性リアクタンス』
リアクタンスに関する例題

などを図を用いて分かりやすく説明しています。

リアクタンスとは

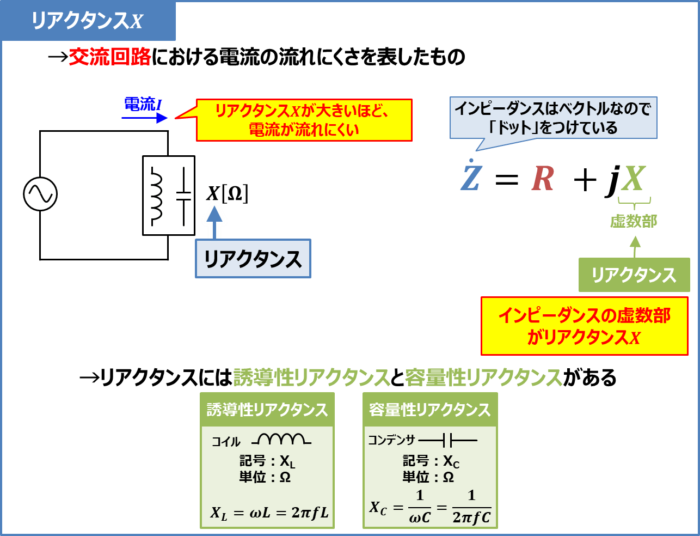
最初にリアクタンスの要点を以下にまとめます。

リアクタンスの要点

リアクタンスは「交流回路における電流の流れにくさを表すもの」であり、記号はX、単位は[Ω]を用いる
リアクタンスが大きいほど電流が流れにくくなる
リアクタンスはインピーダンス(Z=R+jX)の虚数部である
『誘導性リアクタンスX_L』と『容量性リアクタンスX_C』がある

各要点について順番に説明します。

リアクタンスは「交流回路における電流の流れにくさを表すもの」であり、記号はX、単位は[Ω]を用いる

リアクタンスは「交流回路における電流の流れにくさ」を表すものです。記号はX、単位は[Ω]を用います。

抵抗Rも「電流の流れにくさ」を表すものですが、抵抗Rは「直流回路と交流回路の両方における電流の流れにくさ」を表すものです。また、「抵抗R、電流I、電圧Vの関係」はオームの法則より次式で表されます。

\begin{eqnarray}
R=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

抵抗Rと同じようにリアクタンスXも「リアクタンスX、電流I、電圧Vの関係」を式で表すことができ、次式で表されます。

\begin{eqnarray}
X=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

例えば、交流電圧源の電圧Vが10[V]であり、この時に流れている電流Iが5[A]の場合、リアクタンスXは2[Ω]となります。

また、リアクタンスX[Ω]と電圧V[V]が分かれば電流I[A]を求めることができ、リアクタンスX[Ω]と電流I[A]が分かれば電圧V[V]を求めることができます。

リアクタンスX[Ω]と電圧V[V]が分かっている時

\begin{eqnarray}
I=\frac{V}{X}{\mathrm{[A]}}
\end{eqnarray}

リアクタンスX[Ω]と電流I[A]が分かっている時

\begin{eqnarray}
V=XI{\mathrm{[V]}}
\end{eqnarray}

リアクタンスが大きいほど電流が流れにくくなる

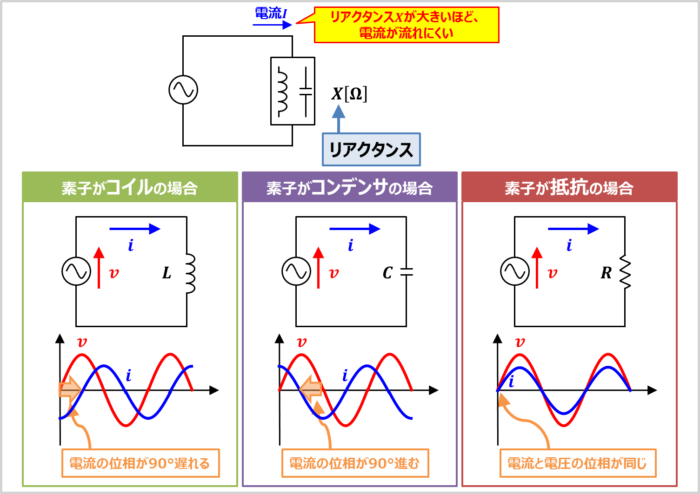
リアクタンスXは「交流回路における電流の流れにくさ」を表しています。そのため、リアクタンスXの大きさにより電流Iは以下のように変わります。

リアクタンスXが大きい

→電流Iが流れにくい

リアクタンスXが小さい

→電流Iが流れやすい

また、リアクタンスX[Ω]と電圧V[V]が分かっている時、流れる電流I[A]は「\(I=\displaystyle\frac{V}{X}{\mathrm{[A]}}\)」であることを説明しました。この式からリアクタンスX[Ω]が大きくなると、電流Iが小さくなることが分かりますね。

なお、交流には位相があります。素子がコイルやコンデンサの場合、電圧と電流の位相にずれが生じます。

素子がコイルの場合

電圧の位相に対して電流の位相が90°遅れます。

素子がコンデンサの時

電圧の位相に対して電流の位相が90°進みます。

素子が抵抗の時

電圧と電流の位相は同じです。

リアクタンスはインピーダンスの虚数部である

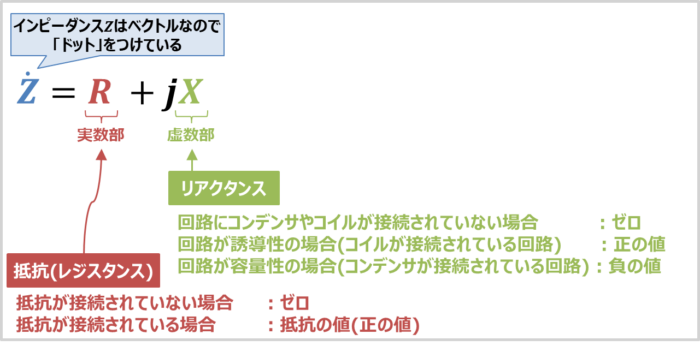
インピーダンスZは抵抗(レジスタンス)RとリアクタンスXを用いると次式で表されます。

\begin{eqnarray}
{\dot{Z}}=R+jX
\end{eqnarray}

上式より、リアクタンスXはインピーダンスZの虚数部であることが分かります。なお、抵抗(レジスタンス)Rは『ゼロ』または『正の値』となります。抵抗が接続されていない場合はゼロとなり、抵抗が接続されている場合は抵抗値の値(正の値)となります。

一方、リアクタンスXは『ゼロ』または『正の値』または『負の値』となります。回路にコイルやコンデンサが接続されていない場合はゼロとなります。また、回路が誘導性の場合(コイルが接続されている回路)は正の値となり、回路が容量性の場合(コンデンサが接続されている回路)は負の値となります。

『誘導性リアクタンスX_L』と『容量性リアクタンスX_C』がある

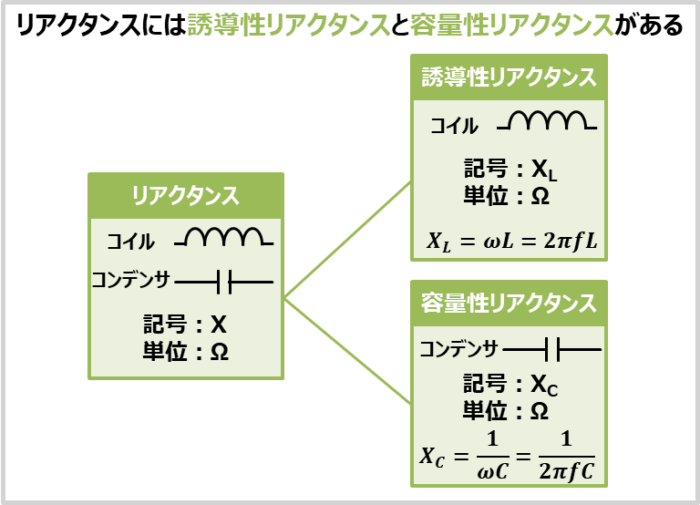
直流回路においては、電流を妨げるものは「抵抗器」が一般的です。一方、交流回路において、電流の流れを妨げるものは「抵抗器」に加えて「コイル(インダクタ)」と「コンデンサ(キャパシタ)」も含まれます。

このコイルとコンデンサの抵抗成分がリアクタンスとなります。なお、コイルのリアクタンスを「誘導性リアクタンス」といい、コンデンサのリアクタンスを「容量性リアクタンス」といいます。

次に『誘導性リアクタンスX_L』と『容量性リアクタンスX_C』について詳しく説明します。

コイルのリアクタンス(誘導性リアクタンス)

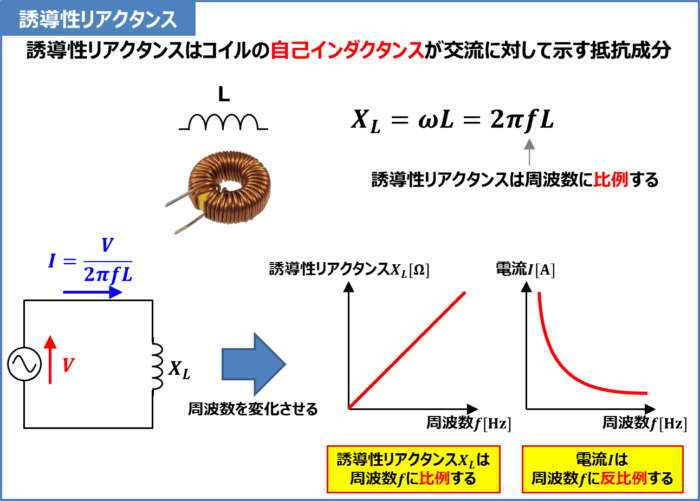
誘導性リアクタンスはコイルの自己インダクタンスが交流に対して示す抵抗成分です。

リアクタンスは記号Xで表しますが、誘導性リアクタンスは自己インダクタンスLによって生じる抵抗成分なので記号X_Lで表されることが多いです。

誘導性リアクタンスX_Lは次式で表されます。

\begin{eqnarray}
X_L={\omega}L=2{\pi}fL
\end{eqnarray}

\({\omega}\)：角周波数(\({\omega}=2{\pi}f\))[rad/s]
\(f\)：周波数[Hz]
\(L\)：コイルのインダクタンス[H](←ヘンリーと読みます)

上式より誘導性リアクタンスは周波数に比例します。そのため、交流回路の周波数が高いほど、誘導性リアクタンスは大きくなります。

なお、周波数fが0[Hz]の場合(直流回路の場合)、誘導性リアクタンスX_Lは0[Ω]となります。すなわち、直流ではコイルはショート状態(短絡状態)とみなすことができます。

また、「誘導性リアクタンスX_L、電流I、電圧Vの関係」は次式で表すことができます。

\begin{eqnarray}
X_L=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

この式を電流の式に置き換えると次式となります。

\begin{eqnarray}
I=\frac{V}{X_L}=\frac{V}{2{\pi}fL}{\mathrm{[A]}}
\end{eqnarray}

すなわち、周波数fが高くなると、誘導性リアクタンスX_Lが大きくなるため、回路に流れる電流Iが小さくなるということが分かります(回路に流れる電流Iは周波数fに反比例します)。

「インダクタンス」と「誘導性リアクタンス」

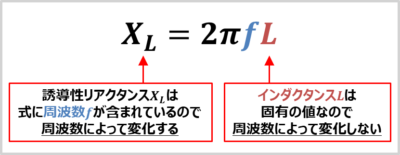
コイルのインダクタンスLはコイルの巻数や形によって決まる固有の値です。そのため、周波数fが変化しても、インダクタンスLは変化しません。

しかし、誘導性リアクタンスX_Lは「\(X_L={\omega}L=2{\pi}fL\)」の式で表れます。そのため、周波数fが変化すると、誘導性リアクタンスX_Lは変化します。

インダクタンスLと誘導性リアクタンスX_Lがごちゃごちゃにならないように注意しましょう。

コンデンサのリアクタンス(容量性リアクタンス)

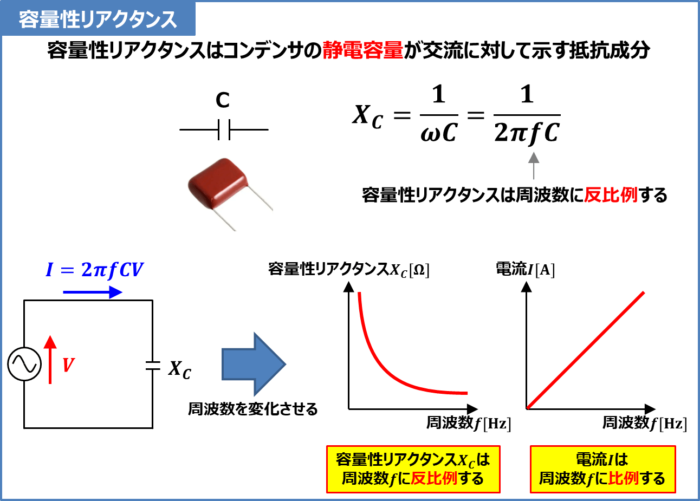
容量性リアクタンスはコンデンサの静電容量(キャパシタンス)が交流に対して示す抵抗成分です。

リアクタンスは記号Xで表しますが、容量性リアクタンスは静電容量Cによって生じる抵抗成分なので記号X_Cで表されることが多いです。

容量性リアクタンスX_Cは次式で表されます。

\begin{eqnarray}
X_C=\frac{1}{{\omega}C}=\frac{1}{2{\pi}fC}{\mathrm{[{\Omega}]}}
\end{eqnarray}

\({\omega}\)：角周波数(\({\omega}=2{\pi}f\))[rad/s]
\(f\)：周波数[Hz]
\(C\)：コンデンサの静電容量(キャパシタンス)[F](←ファラドと読みます)

上式より容量性リアクタンスは周波数に反比例します。そのため、交流回路の周波数が高いほど、容量性リアクタンスは小さくなります。

なお、周波数fが0[Hz]の場合(直流回路の場合)、容量性リアクタンスX_Cは∞[Ω](無限大)となります。すなわち、直流ではコンデンサはオープン状態(開放状態)とみなすことができます。

また、「容量性リアクタンスX_L、電流I、電圧Vの関係」は次式で表すことができます。

\begin{eqnarray}
X_C=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

この式を電流の式に置き換えると次式となります。

\begin{eqnarray}
I=\frac{V}{X_C}=2{\pi}fCV{\mathrm{[A]}}
\end{eqnarray}

すなわち、周波数fが高くなると、容量性リアクタンスX_Cが小さくなるため、回路に流れる電流Iが大きくなるということが分かります(回路に流れる電流Iは周波数fに比例します)。

「静電容量(キャパシタンス)」と「容量性リアクタンス」

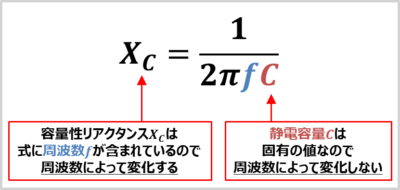
コイルの静電容量(キャパシタンス)Cはコンデンサによって決まる固有の値です。そのため、周波数fが変化しても、静電容量Cは変化しません。

しかし、容量性リアクタンスX_Cは「\(X_C=\displaystyle\frac{1}{{\omega}C}=\displaystyle\frac{1}{2{\pi}fC}\)」の式で表れます。そのため、周波数fが変化すると、容量性リアクタンスX_Cは変化します。

静電容量(キャパシタンス)Cと容量性リアクタンスX_Cがごちゃごちゃにならないように注意しましょう。

合成リアクタンス

『誘導性リアクタンスX_L』と『容量性リアクタンスX_C』の差を合成リアクタンスXということがあります。

合成リアクタンスは次式で表されます。

\begin{eqnarray}
X=X_L-X_C{\mathrm{[{\Omega}]}}
\end{eqnarray}

リアクタンスに関する例題

例題1

上図に示す周波数f=50[Hz],V=90[V]の交流電圧源に自己インダクタンスL=0.1[H]のコイルを接続した回路において、以下のものを求めてみましょう。なお、π=3とします。

誘導性リアクタンスX_Lの大きさ
回路に流れる電流I
交流電圧源Eと回路に流れる電流Iの位相差θ

解答

誘導性リアクタンスX_Lの大きさ

誘導性リアクタンスX_Lは以下の値となります。

\begin{eqnarray}
X_L&=&2{\pi}fL
&=&2×3×50×0.1
&=&30{\mathrm{[{\Omega}]}}
\end{eqnarray}

回路に流れる電流I

回路に流れる電流Iは以下の値となります。

\begin{eqnarray}
I=\frac{V}{X_L}=\frac{90}{30}=30{\mathrm{[A]}}
\end{eqnarray}

交流電圧源Eと回路に流れる電流Iの位相差θ

回路に流れる電流Iは交流電圧源Eより\({\theta}=\displaystyle\frac{{\pi}}{2}\)遅れる。

例題2

上図に示す周波数f=50[Hz],V=200[V]の交流電圧源に静電容量C=100[μF]のコンデンサを接続した回路において、以下のものを求めてみましょう。なお、π=3とします。

容量性リアクタンスX_Cの大きさ
回路に流れる電流I
交流電圧源Eと回路に流れる電流Iの位相差θ

解答

誘導性リアクタンスX_Lの大きさ

誘導性リアクタンスX_Lは以下の値となります。

\begin{eqnarray}
X_C&=&\frac{1}{2{\pi}fC}\\
&=&\frac{1}{2×3×50×100×10^{-6}}\\
&=&\frac{100}{3}{\mathrm{[{\Omega}]}}
\end{eqnarray}

回路に流れる電流I

回路に流れる電流Iは以下の値となります。

\begin{eqnarray}
I=\frac{V}{X_C}=\frac{200}{\displaystyle\frac{100}{3}}=6{\mathrm{[A]}}
\end{eqnarray}

交流電圧源Eと回路に流れる電流Iの位相差θ

回路に流れる電流Iは交流電圧源Eより\({\theta}=\displaystyle\frac{{\pi}}{2}\)進む。

まとめ

この記事では『リアクタンス』について、以下の内容を説明しました。

リアクタンスとは
リアクタンスの特徴
『誘導性リアクタンス』と『容量性リアクタンス』
リアクタンスに関する例題

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。

全記事一覧

【リアクタンスとは】『単位』や『計算方法』などのまとめ！

リアクタンスとは