この記事では『プリント基板の銅箔抵抗』について
- プリント基板の銅箔抵抗の計算
- プリント基板の銅箔抵抗の計算(温度を考慮した時)
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
プリント基板の銅箔抵抗
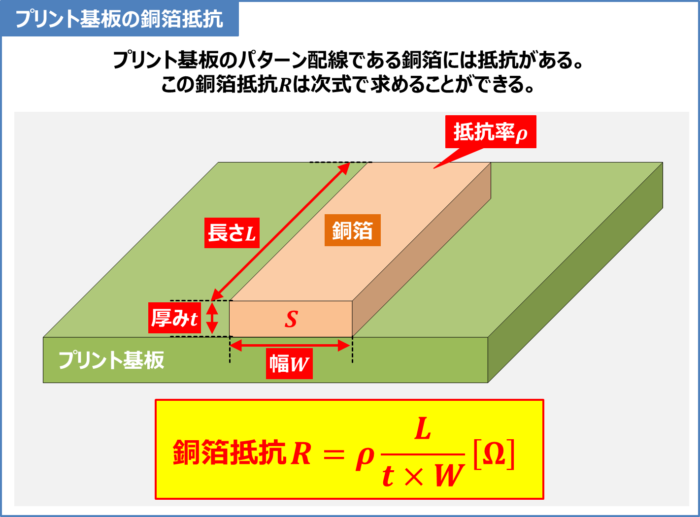
プリント基板のパターン配線である銅箔には抵抗があります。この抵抗は銅箔抵抗と呼ばれています。
導体の抵抗値\(R{\mathrm{[{\Omega}]}}\)は導体の長さ\(L{\mathrm{[m]}}\)に比例し、導体の断面積\(S{\mathrm{[m^2]}}\)に反比例するため、次式で表されます。
\begin{eqnarray}
R={\rho}\frac{L}{S}{\mathrm{[{\Omega}]}}\tag{1}
\end{eqnarray}
(1)式の「\(\displaystyle\frac{L}{S}\)」の前についている比例定数\({\rho}\)は抵抗率と呼ばれており、単位は\({\mathrm{[{\Omega}{\;}{\cdot}{\;}m]}}\)となります。
ここで、温度が25℃の時の銅箔の抵抗率を\({\rho}=1.7×10^{-8}{\mathrm{[{\Omega}{\;}{\cdot}{\;}m]}}\)、銅箔の長さを\(L{\mathrm{[m]}}\)、銅箔の厚みを\(t{\mathrm{[m]}}\)、銅箔の幅を\(W{\mathrm{[m]}}\)とすると、銅箔の断面積\(S{\mathrm{[m^2]}}\)は「\(S=t×W{\mathrm{[m^2]}}\)」となるため、プリント基板の銅箔抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表すことができます。
\begin{eqnarray}
R&=&{\rho}\frac{L}{S}\\
\\
&=&{\rho}\frac{L}{t×W}\\
\\
&=&1.7×10^{-8}×\frac{L}{t×W}{\mathrm{[{\Omega}]}}\tag{2}
\end{eqnarray}
(2)式から分かるように、プリント基板の銅箔抵抗\(R\)は銅箔の長さ\(L\)・厚み\(t\)・幅\(W\)によって変化します。
では、実際に銅箔抵抗\(R\)を計算してみましょう。例えば、
- 銅箔の長さ:\(L=1{\mathrm{[cm]}}=1×10^{-2}{\mathrm{[m]}}\)
- 銅箔の厚み:\(t=35{\mathrm{[μm]}}=35×10^{-6}{\mathrm{[m]}}\)
- 銅箔の幅:\(W=1{\mathrm{[mm]}}=1×10^{-3}{\mathrm{[m]}}\)
の時、銅箔抵抗\(R\)は以下の値になります。
\begin{eqnarray}
R&=&1.7×10^{-8}×\frac{L}{t×W}{\mathrm{[{\Omega}]}}\\
\\
&=&1.7×10^{-8}×\frac{1×10^{-2}}{(35×10^{-6})×(1×10^{-3})}{\mathrm{[{\Omega}]}}\\
\\
&=&4.86×10^{-3}{\mathrm{[{\Omega}]}}\\
\\
&=&4.86{\mathrm{[m{\Omega}]}}\tag{3}
\end{eqnarray}
例えば、この銅箔(パターン)に\(3{\mathrm{[A]}}\)の電流\(I\)が流れていたとすると、銅箔による電圧降下\(V\)はオームの法則より以下の値になります。
\begin{eqnarray}
V&=&RI\\
\\
&=&4.86×10^{-3}×3\\
\\
&=&14.58×10^{-3}{\mathrm{[V]}}\\
\\
&=&14.58{\mathrm{[mV]}}\tag{4}
\end{eqnarray}
また、この時、銅箔で生じる導通損失\(P\)は以下の値になります。
\begin{eqnarray}
P&=&RI^2\\
\\
&=&4.86×10^{-3}×3^2\\
\\
&=&43.74×10^{-3}{\mathrm{[W]}}\\
\\
&=&43.74{\mathrm{[mW]}}\tag{5}
\end{eqnarray}
このように、プリント基板に電流\(I\)が流れると、銅箔抵抗\(R\)によって、電圧降下\(V\)が生じます。また、導通損失\(P\)により銅箔が発熱します。そのため、大電流が流れる銅箔(パターン)に関しては、銅箔抵抗\(R\)を考慮する必要があります。
補足
プリント基板の銅箔の厚み\(t\)は18μm・35μm・70μmが一般的に使われています。
あわせて読みたい
『抵抗率\({\rho}\)』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
【抵抗率とは】『単位』や『導電率との違い』などを解説!
プリント基板の銅箔抵抗(温度による影響を考慮した場合)
(3)式~(5)式はプリント基板の温度が25℃の時における銅箔抵抗\(R\)・電圧降下\(V\)・導通損失\(P\)となります。銅は温度が上昇すると、銅箔抵抗\(R\)が増加する特徴を持っているため、厳密には温度による影響を考慮する必要があります。
温度による抵抗値の変化は抵抗温度係数\(α\)を用いて計算することができます。銅の抵抗温度係数を「\(α=0.000393\)」とすると、温度\(t{\mathrm{[{^{\circ}C}]}}\)の時におけるプリント基板の銅箔抵抗\(R_t{\mathrm{[{\Omega}]}}\)は次式で表すことができます。
\begin{eqnarray}
R_t&=&{\rho}\frac{L}{t×W}[1+α(t-25)]{\mathrm{[{\Omega}]}}\\
\\
&=&1.7×10^{-8}×\frac{L}{t×W}[1+0.00393(t-25)]{\mathrm{[{\Omega}]}}\tag{6}
\end{eqnarray}
では、実際に温度を考慮した時の銅箔抵抗\(R_t\)を計算してみましょう。例えば、
- 銅箔の長さ:\(L=1{\mathrm{[cm]}}=1×10^{-2}{\mathrm{[m]}}\)
- 銅箔の厚み:\(t=35{\mathrm{[μm]}}=35×10^{-6}{\mathrm{[m]}}\)
- 銅箔の幅:\(W=1{\mathrm{[mm]}}=1×10^{-3}{\mathrm{[m]}}\)
とすると、温度が「\(t=100{\mathrm{[{^{\circ}C}]}}\)」の時の銅箔抵抗\(R_{100}\)は以下の値になります。
\begin{eqnarray}
R_{100}&=&1.7×10^{-8}×\frac{L}{t×W}[1+0.00393(t-25)]{\mathrm{[{\Omega}]}}\\
\\
&=&1.7×10^{-8}×\frac{1×10^{-2}}{(35×10^{-6})×(1×10^{-3})}[1+0.00393(100-25)]{\mathrm{[{\Omega}]}}\\
\\
&=&6.29×10^{-3}{\mathrm{[{\Omega}]}}\\
\\
&=&6.29{\mathrm{[m{\Omega}]}}\tag{7}
\end{eqnarray}
そのため、温度が「\(t=100{\mathrm{[{^{\circ}C}]}}\)」の時において、銅箔(パターン)に\(3{\mathrm{[A]}}\)の電流\(I\)が流れていたとすると、銅箔による電圧降下\(V\)はオームの法則より以下の値になります。
\begin{eqnarray}
V&=&R_{100}I\\
\\
&=&6.29×10^{-3}×3\\
\\
&=&18.87×10^{-3}{\mathrm{[V]}}\\
\\
&=&18.87{\mathrm{[mV]}}\tag{8}
\end{eqnarray}
また、この時、銅箔で生じる導通損失\(P\)は以下の値になります。
\begin{eqnarray}
P&=&R_{100}I^2\\
\\
&=&6.29×10^{-3}×3^2\\
\\
&=&56.61×10^{-3}{\mathrm{[W]}}\\
\\
&=&56.61{\mathrm{[mW]}}\tag{9}
\end{eqnarray}
(8)式と(9)式から分かるように、温度が上がると、銅箔での電圧降下\(V\)や導通損失\(P\)が増加します。
銅箔の幅\(W\)を広くすれば、銅箔抵抗\(R\)が小さくなるため、電圧降下\(V\)や導通損失\(P\)を減らすことができますが、銅箔の幅\(W\)が広い場合、プリント基板上の銅箔の専有面積が増えてしまいますので、広くすれば良いということではありません。
あわせて読みたい
『抵抗温度係数\(α\)』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る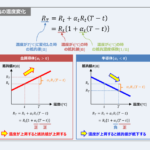


抵抗の温度特性について!抵抗温度係数ってなに?
まとめ
この記事では『プリント基板の銅箔抵抗』について、以下の内容を説明しました。
- プリント基板の銅箔抵抗の計算
- プリント基板の銅箔抵抗の計算(温度を考慮した時)
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






