【相互インダクタンスとは】『単位』や『例題』などを解説！

この記事では相互インダクタンスについて

相互インダクタンスとは
相互インダクタンスの『単位』
相互インダクタンスと誘導起電力
相互インダクタンスに関する例題

などを図を用いて分かりやすく説明しています。

相互インダクタンスとは

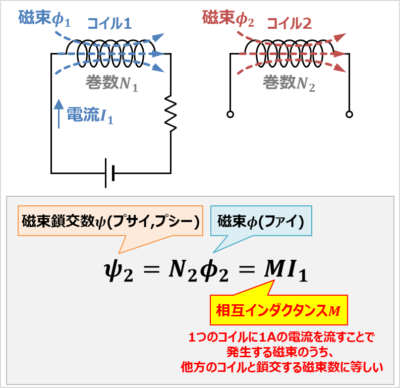
上図に示すように、巻数\(N_1\)のコイル1と巻数\(N_2\)のコイル2が近い位置にある時、コイル1に電流\(I_1{\mathrm{[A]}}\)を流した時、この電流\(I_1\)によってできる磁束\({\phi}_1\)の一部がコイル2を通ります。

このコイル2を通る磁束を\({\phi}_2{\mathrm{[wb]}}\)、磁束鎖交数を\({\psi}_2{\mathrm{[wb]}}\)とすると、磁束鎖交数\({\psi}_2\)は電流\(I_1\)に比例するため、次式で表されます。

\begin{eqnarray}
{\psi}_2=N_2{\phi}_2=MI_1\tag{1}
\end{eqnarray}

(1)式において、比例定数\(M\)が相互インダクタンスとなります。

(1)式より、コイルの相互インダクタンス\(M\)は1つのコイルに1Aの電流を流すことで発生する磁束のうち、他方のコイルと鎖交する磁束数に等しいということが分かります。

磁束鎖交数Ψと磁束Φの記号について

磁束鎖交数と磁束の記号は参考書やネットによって様々であり、磁束鎖交数の記号を\({\phi}\)(ファイ)や\({\psi}\)(プサイ,プシー)で表している場合もあります。

このサイトでは、

磁束鎖交数の記号：\({\psi}\)(プサイ,プシー)
磁束の記号；\({\phi}\)(ファイ)

で表示しています。

補足

相互インダクタンス\(L\)は『相互誘導係数』とも呼ばれています。

相互インダクタンスの『単位』

(1)式において、相互インダクタンス\(M\)の式に変形すると、次式となります。

\begin{eqnarray}
M=\frac{{\psi}_2}{I_1}=\frac{N_2{\phi}_2}{I_1}\tag{2}
\end{eqnarray}

(2)式において、磁束鎖交数\({\psi}_2\)の単位は\({\mathrm{[wb]}}\)であり、電流\(I_1\)の単位は\({\mathrm{[A]}}\)となるため、相互インダクタンス\(M\)の単位は\({\mathrm{[wb/A]}}\)となりますが、電気の世界では相互インダクタンス\(M\)の単位を\({\mathrm{[H]}}\)(←ヘンリー)とします。

相互インダクタンスと誘導起電力

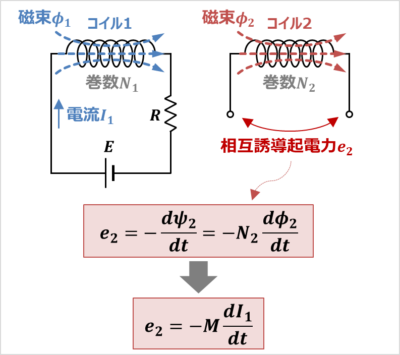
上図において、抵抗\(R\)の値や電圧源\(E\)の値を変えることによって、コイル1に流れる電流\(I_1\)を変化させると、コイル2の磁束鎖交数\({\psi}_2\)が変化します。その結果、コイル2に相互誘導起電力\(e_2\)が発生します。

相互誘導起電力\(e_2\)は次式で表されます。

\begin{eqnarray}
e_2=-\frac{d{\psi}_2}{dt}=-N_2\frac{d{\phi}_2}{dt}{\mathrm{[V]}}\tag{3}
\end{eqnarray}

この現象を相互誘導といいます。

ここで、(3)式に(1)式を代入すると、次式となります。

\begin{eqnarray}
e_2=-M\frac{dI_1}{dt}{\mathrm{[V]}}\tag{4}
\end{eqnarray}

(4)式より、コイルの相互インダクタンス\(M\)は1つのコイルに流れる電流を1秒間に1Aの割合で変化させた時において、他のコイルに発生する相互誘導起電力に等しいということが分かります。

つまり、相互インダクタンス\(M\)とは、コイルに生じる相互誘導起電力の大きさの目安を表す量であり、\(M\)が大きいほど、相互誘導起電力が大きくなります。

補足

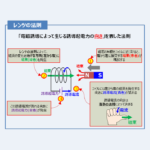
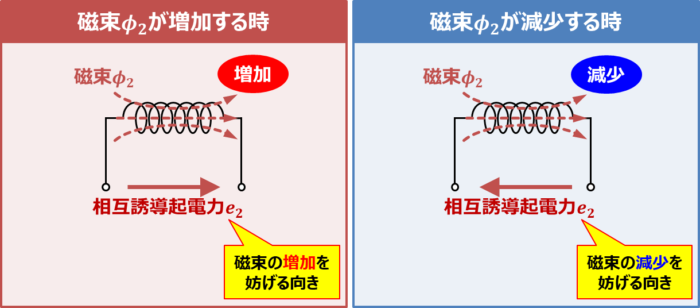
相互誘導起電力\(e_2\)はレンツの法則により、磁束\({\phi}_2\)の変化を妨げる方向となります。

磁束\({\phi}_2\)が増加する時

磁束\({\phi}_2\)の増加を妨げる向きに相互誘導起電力\(e_2\)が発生します。

磁束\({\phi}_2\)が減少する時

磁束\({\phi}_2\)の減少を妨げる向きに相互誘導起電力\(e_2\)が発生します。

そのため、(3)式と(4)式に「－(マイナス)」が付いています。

なお、レンツの法則については詳しくは以下の記事で説明していますので、参考にしてください。

: 【レンツの法則とは】起電力の向きについてわかりやすく解説！
続きを見る

相互インダクタンスに関する例題

では、これから相互インダクタンスに関する問題を2つ解いてみましょう。

相互インダクタンスに関する例題(その1)

問題文

巻数\(N_1=50\)のコイル1と巻数\(N_2=100\)のコイル2があり、コイル1に電流\(I_1=0.5{\mathrm{[A]}}\)を流すと、コイル2に\(3×10^{-4}{\mathrm{[wb]}}\)の磁束が鎖交する。この時の相互インダクタンス\(M\)を求めよ。

回答

相互インダクタンス\(M\)は(1)式を用いると以下の値となります。

\begin{eqnarray}
M&=&\frac{N_2{\phi}_2}{I_1}\\
&=&\frac{100×3×10^{-4}}{0.5}\\
&=&0.06{\mathrm{[H]}}
\end{eqnarray}

相互インダクタンスに関する例題(その2)

問題文

2つのコイルがあり、相互インダクタンス\(M\)が\(0.5{\mathrm{[H]}}\)とする。この時、コイル1に流れる電流\(I_1\)が\(0.2{\mathrm{[s]}}\)に\(3{\mathrm{[A]}}\)から\(1{\mathrm{[A]}}\)に変化した時、コイル2に発生する起電力\(e_2\)は何ボルトか？

回答

コイル2に発生する起電力\(e_2\)は(4)式を用いると以下の値となります。

\begin{eqnarray}
e_2&=&-M\frac{dI_1}{dt}{\mathrm{[V]}}\\
&=&-0.5×\frac{1-3}{0.2}\\
&=&5{\mathrm{[V]}}
\end{eqnarray}