ミルマンの定理とは？『公式の覚え方』や『例題』などを解説！

この記事では『ミルマンの定理』について

ミルマンの定理とは
ミルマンの定理の『公式の覚え方』と『例題』
ミルマンの定理とオームの法則の関係

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

ミルマンの定理とは

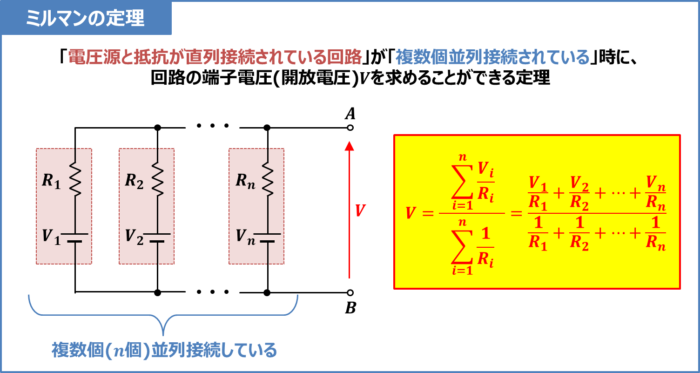
ミルマンの定理とは、「電圧源と抵抗が直列接続されている回路」が「複数個並列接続されている」時に、回路の端子電圧(開放電圧)\(V\)を求めることができる定理です。

例えば、上図に示すような「電圧源と抵抗が直列接続されている回路」が「\(n\)個並列接続されている」時、この回路の端子電圧(開放電圧)\(V\)は次式で表されます。

ミルマンの定理の公式

\begin{eqnarray}
V=\frac{\displaystyle\sum_{i=1}^n\displaystyle\frac{V_i}{R_i}}{\displaystyle\sum_{i=1}^n\displaystyle\frac{1}{R_i}}=\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{V_n}{R_n}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{1}{R_n}}\tag{1}
\end{eqnarray}

補足

ミルマンの定理は「全電圧の定理」や「帆足(ほあし)・ミルマンの定理」とも呼ばれています。
ミルマンの定理は英語では「Millman"s Theorem」と書きます。

ミルマンの定理の覚え方

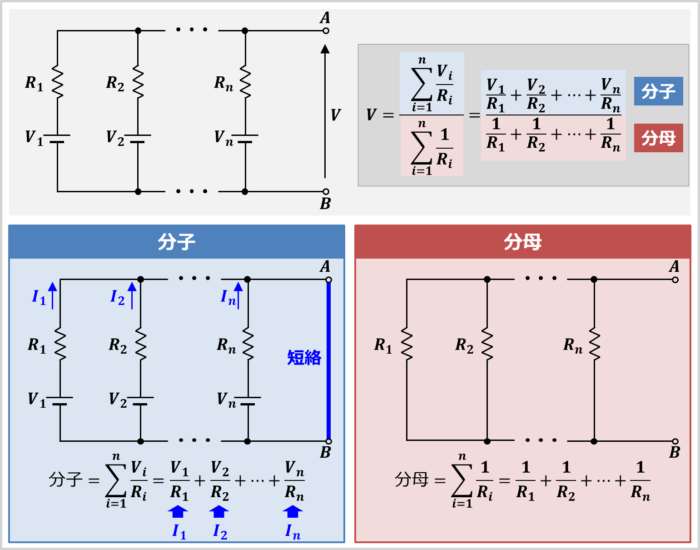
ミルマンの定理は覚えるのが大変ですが、分子と分母に分けて考えると覚えやすくなります。

分子

分子は次式となっており、「端子A-B間を短絡した時に流れる合成電流」を意味しています。

\begin{eqnarray}
(1)式の分子=\displaystyle\sum_{i=1}^n\displaystyle\frac{V_i}{R_i}=\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{V_n}{R_n}\tag{2}
\end{eqnarray}

分母

分母は次式となっており、「電圧源を取り除いた後の端子A-B間の合成抵抗の逆数(合成コンダクタンス)」を意味しています。

\begin{eqnarray}
(1)式の分母=\displaystyle\sum_{i=1}^n\displaystyle\frac{1}{R_i}=\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{1}{R_n}\tag{3}
\end{eqnarray}

このようにミルマンの定理において、「分子は短絡した時に流れる合成電流」、「分母は合成抵抗の逆数(合成コンダクタンス)」と考えると覚えやすくなります。

「ミルマンの定理」と「オームの法則」

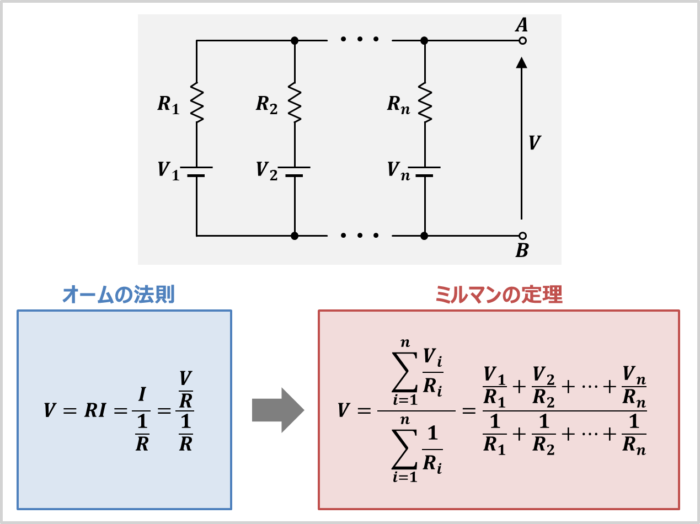
ミルマンの定理がやっていることは「オームの法則(\(V=RI\))」と変わりはありません。「オームの法則」を変形させると、次式に示すように「ミルマンの定理」となります。

\begin{eqnarray}
V&=&RI=\frac{I}{\displaystyle\frac{1}{R}}=\frac{\displaystyle\frac{V}{R}}{\displaystyle\frac{1}{R}}{\;}{\;}{\Rightarrow}{\;}{\;}V&=&\frac{\displaystyle\sum_{i=1}^n\displaystyle\frac{V_i}{R_i}}{\displaystyle\sum_{i=1}^n\displaystyle\frac{1}{R_i}}=\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{V_n}{R_n}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{1}{R_n}}\tag{4}
\end{eqnarray}

ミルマンの定理の例題

先ほど説明した回路だと、全ての枝で電圧源と抵抗が直列接続されていました。しかし、実際の回路では電圧源の数が少なかったり、逆向きの電源があったりしますよね。

なので、次に

「電圧源：3個」、「抵抗：3個」の回路の場合
「電圧源：2個」、「抵抗：3個」の回路の場合(←電圧源が少ない場合)
「逆向きの電源」がある回路の場合

の3パターンにおいて、ミルマンの定理の例題を解いてみましょう。

「電圧源：3個」、「抵抗：3個」の回路の場合

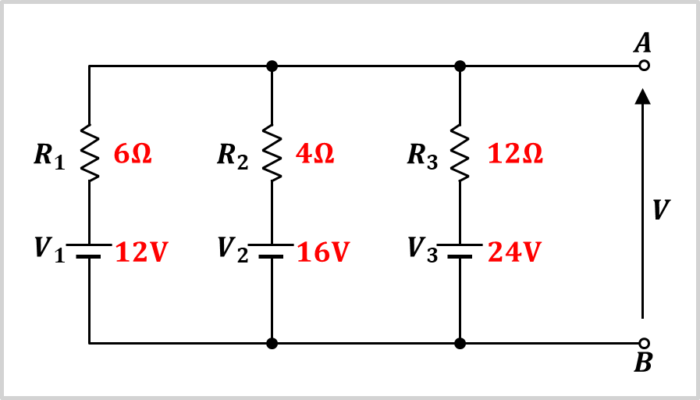
上図に示す回路の端子電圧(開放電圧)\(V\)は何\(V\)でしょうか。

解答

ミルマンの定理の公式は次式で表されます。

ミルマンの定理の公式

上図に示す回路では、各枝には全て電圧源と抵抗が直列接続されており、また、逆向きの電源もないため、電圧源\(V_1\),\(V_2\),\(V_3\)、抵抗\(R_1\),\(R_2\),\(R_3\)に各値を代入すると、端子電圧\(V\)を求めることができ、以下の値となります。

\begin{eqnarray}
V&=&\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+\displaystyle\frac{V_3}{R_3}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
\\
&=&\frac{\displaystyle\frac{12}{6}+\displaystyle\frac{16}{4}+\displaystyle\frac{24}{12}}{\displaystyle\frac{1}{6}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{12}}\\
\\
&=&\frac{2+4+2}{\displaystyle\frac{2+3+1}{12}}\\
\\
&=&\frac{8}{0.5}\\
\\
&=&16{\mathrm{[V]}}\tag{5}
\end{eqnarray}

「電圧源：2個」、「抵抗：3個」の回路の場合(←電圧源が少ない場合)

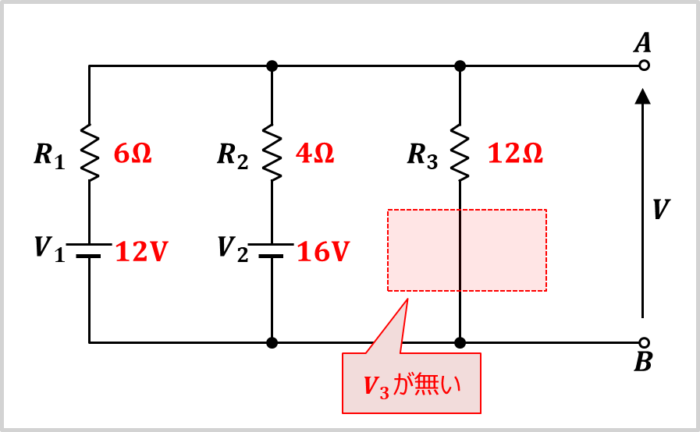
上図に示す回路の端子電圧(開放電圧)\(V\)は何\(V\)でしょうか。

解答

ミルマンの定理の公式は次式で表されます。

ミルマンの定理の公式

上図に示す回路には、電圧源が1個ありません。電圧源\(V_3\)が無くなっています。この場合、電圧源がないところには\(0{\mathrm{[V]}}\)の電圧源があるものと考えます(\(V_3=0{\mathrm{[V]}}\))。そのため、上式において、電圧源\(V_1\),\(V_2\)、抵抗\(R_1\),\(R_2\),\(R_3\)に各値を代入すると、端子電圧\(V\)を求めることができ、以下の値となります。

\begin{eqnarray}
V&=&\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+\displaystyle\frac{V_3}{R_3}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
\\
&=&\frac{\displaystyle\frac{12}{6}+\displaystyle\frac{16}{4}+\displaystyle\frac{0}{12}}{\displaystyle\frac{1}{6}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{12}}\\
\\
&=&\frac{2+4}{\displaystyle\frac{2+3+1}{12}}\\
\\
&=&\frac{6}{0.5}\\
\\
&=&12{\mathrm{[V]}}\tag{6}
\end{eqnarray}

「逆向きの電源」がある回路の場合

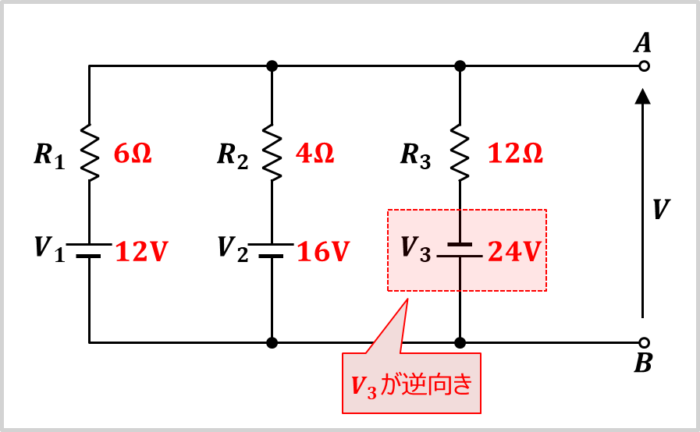
上図に示す回路の端子電圧(開放電圧)\(V\)は何\(V\)でしょうか。

解答

ミルマンの定理の公式は次式で表されます。

ミルマンの定理の公式

上図に示す回路では、「電圧源\(V_3\)の向き」は「他の電圧源\(V_1\)および\(V_2\)の向き」と比較すると、逆向きになっています。この場合、逆向きになってる電圧源にはマイナスの値を代入します。 (\(V_3=-24{\mathrm{[V]}}\))。そのため、上式において、電圧源\(V_1\),\(V_2\),\(V_3\)、抵抗\(R_1\),\(R_2\),\(R_3\)に各値を代入すると、端子電圧\(V_{AB}\)を求めることができ、以下の値となります。

\begin{eqnarray}
V&=&\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+\displaystyle\frac{V_3}{R_3}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
\\
&=&\frac{\displaystyle\frac{12}{6}+\displaystyle\frac{16}{4}+\displaystyle\frac{-24}{12}}{\displaystyle\frac{1}{6}+\displaystyle\frac{1}{4}+\displaystyle\frac{1}{12}}\\
\\
&=&\frac{2+4-2}{\displaystyle\frac{2+3+1}{12}}\\
\\
&=&\frac{4}{0.5}\\
\\
&=&8{\mathrm{[V]}}\tag{7}
\end{eqnarray}

ミルマンの定理(負荷抵抗\(R_L\)が接続されている時)

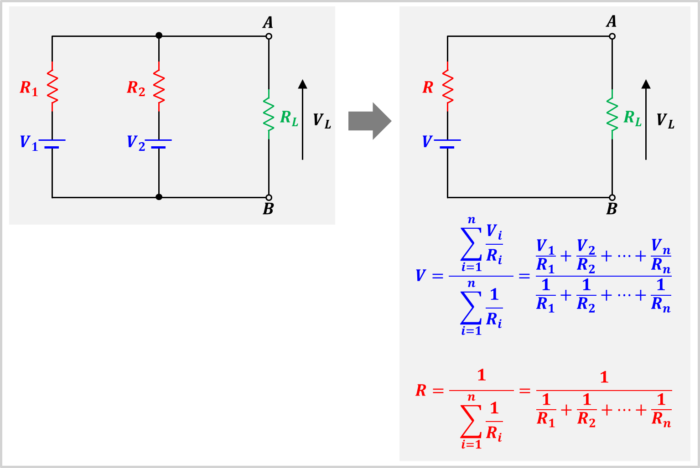
今までは、負荷が開放されている時の端子電圧(開放電圧)\(V\)を計算しましたが、負荷に抵抗\(R_L\)が接続されていても、負荷にかかる電圧\(V_L\)を求めることができます。

上図に示すように、回路に負荷抵抗\(R_L\)が接続されている時、等価電圧源\(V\)と等価抵抗\(R\)は次式で表されます。

\begin{eqnarray}
V&=&\frac{\displaystyle\sum_{i=1}^n\displaystyle\frac{V_i}{R_i}}{\displaystyle\sum_{i=1}^n\displaystyle\frac{1}{R_i}}=\frac{\displaystyle\frac{V_1}{R_1}+\displaystyle\frac{V_2}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{V_n}{R_n}}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{1}{R_n}}\tag{8}\\
\\
R&=&\frac{1}{\displaystyle\sum_{i=1}^n\displaystyle\frac{1}{R_i}}=\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+{\;}{\cdots}{\;}+\displaystyle\frac{1}{R_n}}\tag{9}
\end{eqnarray}

したがって、負荷抵抗\(R_L\)にかかる電圧\(V_L\)は次式で表されます。

\begin{eqnarray}
V_L=\frac{R_L}{R+R_L}V\tag{10}
\end{eqnarray}