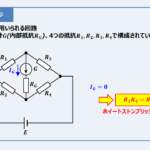
この記事では『メートルブリッジ』について
- メートルブリッジとは
- メートルブリッジの『平衡条件』・『原理』・『例題』
- 『メートルブリッジ』と『ホイートストンブリッジ』の違い
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
メートルブリッジとは
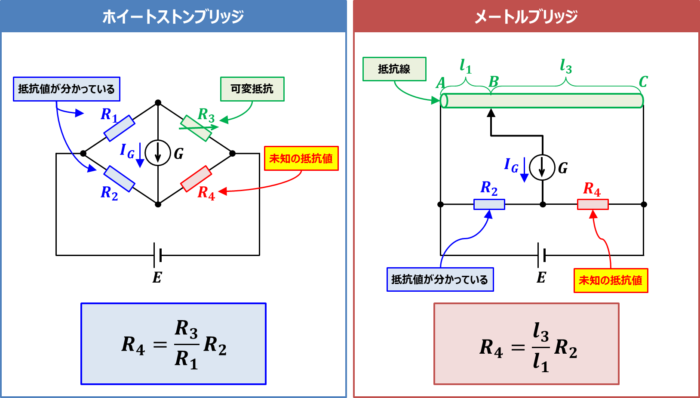
ホイートストンブリッジと同様の原理で抵抗値を測定できる回路に『メートルブリッジ』があります。
ホイートストンブリッジとは、電圧源\(E\)、検流計\(G\)、抵抗値が分かっている抵抗\(R_1\)と\(R_2\)、抵抗値を調整することができる可変抵抗\(R_3\)、抵抗値が未知の抵抗\(R_4\)から構成されている回路です。
可変抵抗\(R_3\)の値を調整して、検流計\(G\)に流れる電流\(I_G\)が0[A]になった時、次式で表される平衡条件が成り立つので、抵抗\(R_4\)の抵抗値を求めることができます。
\begin{eqnarray}
R_1R_4&=&R_2R_3\\
\\
{\Leftrightarrow}R_4&=&\frac{R_3}{R_1}R_2\tag{1}
\end{eqnarray}
一方、メートルブリッジは、電圧源\(E\)、検流計\(G\)、抵抗値が分かっている抵抗\(R_2\)、材質と太さが一様な抵抗線、抵抗値が未知の抵抗\(R_4\)から構成されている回路です。
抵抗線と検流計を接続する箇所をスライドさせ、検流計\(G\)に流れる電流\(I_G\)が0[A]になった時(この時、AB間の長さが\(l_1\)、BC間の長さが\(l_3\)とする)、次式で表される平衡条件が成り立つので、抵抗\(R_4\)の抵抗値を求めることができます。
\begin{eqnarray}
l_1R_4&=&R_2l_3\\
\\
R_4&=&\frac{l_3}{l_1}R_2\tag{2}
\end{eqnarray}
あわせて読みたい
ホイートストンブリッジについては下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

ホイートストンブリッジとは?平衡条件などを解説!
続きを見る
メートルブリッジとホイートストンブリッジの違い
メートルブリッジでは、ホイートストンブリッジで必要だった可変抵抗を用いずに、未知の抵抗値を測定することができます。
また、ホイートストンブリッジでは抵抗値が分かっている抵抗は\(R_1\)と\(R_2\)が必要でしたが、メートルブリッジでは、抵抗\(R_2\)のみ抵抗値が分かって入ればOKです。
その代わりに、材質と太さが一様の抵抗線が必要となります。
メートルブリッジの原理
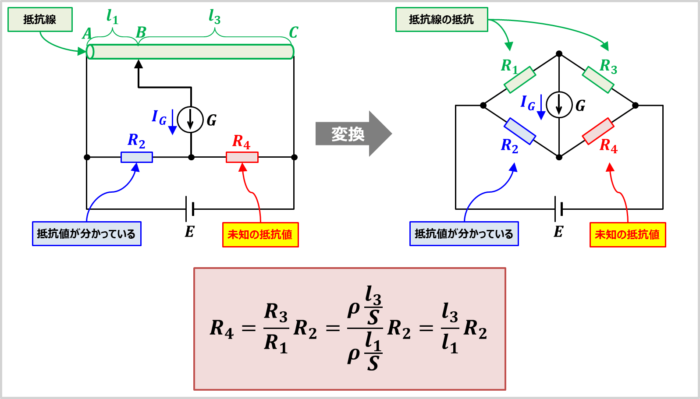

抵抗線の抵抗値\(R\)は抵抗線の長さ\(L\)に比例し、抵抗線の断面積\(S\)に反比例するため、次式で表されます。
\begin{eqnarray}
R={\rho}\frac{L}{S}\tag{3}
\end{eqnarray}
上式の\(\displaystyle\frac{L}{S}\)の前に付いている比例定数が抵抗率\({\rho}\)です。メートルブリッジでは、材質と太さが一様の抵抗線を用いているので、AB間とBC間は抵抗線の断面積\(S\)と抵抗率\({\rho}\)が等しくなります。
したがって、AB間の長さが\(l_1\)、BC間の長さが\(l_3\)の時、AB間の抵抗値\(R_1\)とBC間の抵抗値\(R_3\)は次式で表されます。
\begin{eqnarray}
R_1&=&{\rho}\frac{l_1}{S}\tag{4}\\
\\
R_3&=&{\rho}\frac{l_3}{S}\tag{5}
\end{eqnarray}
(4)式と(5)式を『ホイートストンブリッジの平衡条件である(1)式』に代入すると、次式が成り立ちます。
\begin{eqnarray}
R_1R_4&=&R_2R_3\\
\\
{\Leftrightarrow}R_4&=&\frac{R_3}{R_1}R_2\\
\\
&=&\frac{{\rho}\displaystyle\frac{l_3}{S}}{{\rho}\displaystyle\frac{l_1}{S}}R_2\\
\\
&=&\frac{l_3}{l_1}R_2\tag{6}
\end{eqnarray}
つまり、メートルブリッジでは、「長さ\(l_1\)と\(l_3\)の比\(\displaystyle\frac{l_3}{l_1}\)」と「抵抗\(R_2\)の抵抗値」が分かれば、抵抗\(R_4\)の抵抗値を求めることができます。
あわせて読みたい
抵抗率は電流の流れにくさを表す比例定数です。
抵抗率については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-



【抵抗率とは】『単位』や『導電率との違い』などを解説!
続きを見る
メートルブリッジの例題
メートルブリッジにおいて、抵抗\(R_4\)の抵抗値を求める例題を解いてみましょう。
例題
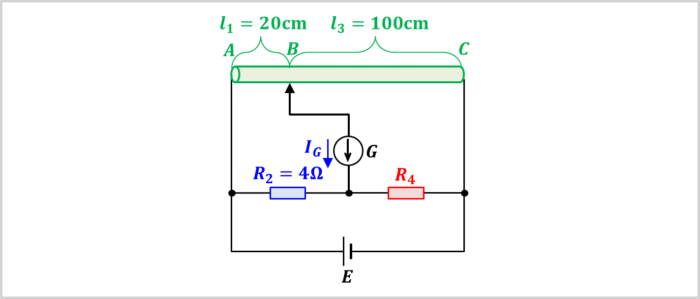

上図に示すようなメートルブリッジにおいて、
- 抵抗\(R_2\)の抵抗値:\(R_2=4Ω\)
- 抵抗線AB間の長さ\(l_1\):\(l_1=20{\mathrm{cm}}\)
- 抵抗線BC間の長さ\(l_3\):\(l_3=100{\mathrm{cm}}\)
の時、検流計\(G\)に流れる電流\(I_G\)が0Aとなった(平衡条件になった)。この時、抵抗\(R_4\)の抵抗値は何Ωでしょうか。
解答
『メートルブリッジの平衡条件である(2)式』に各値を代入すると、抵抗\(R_4\)の抵抗値は以下の値となります。
\begin{eqnarray}
R_4=\frac{l_3}{l_1}R_2=\frac{100}{20}×4=20{\mathrm{[{\Omega}]}}\tag{7}
\end{eqnarray}
まとめ
この記事では『メートルブリッジ』について、以下の内容を説明しました。
- メートルブリッジとは
- メートルブリッジの『平衡条件』・『原理』・『例題』
- 『メートルブリッジ』と『ホイートストンブリッジ』の違い
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。