【ローレンツ力のまとめ】『向き』・『公式』・『円運動』などを解説！

この記事ではローレンツ力について

ローレンツ力とは
ローレンツ力の『向き』
ローレンツ力の『公式』と『大きさ』
ローレンツ力による円運動
ローレンツ力と電磁力の関係

などを図を用いて分かりやすく説明しています。

ローレンツ力とは

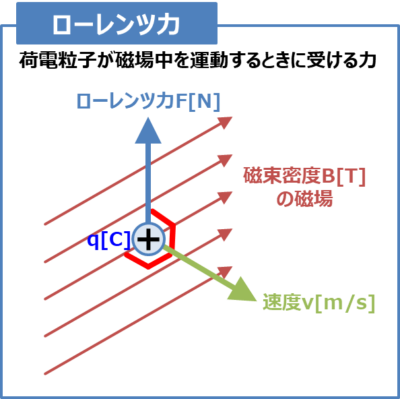
ローレンツ力とは、荷電粒子が磁場中を運動するときに受ける力です。

上図に示しているように、電気量\(+q{\mathrm{[C]}}\)の荷電粒子が速度\(v{\mathrm{[m/s]}}\)で磁束密度\(B{\mathrm{[T]}}\)の磁場中を磁場と垂直な向きで運動している時、荷電粒子は磁場の向きと速度の向きの両方に垂直な向きにローレンツ力\(F{\mathrm{[N]}}\)を受けます。

次に、ローレンツ力の向きはどのように決まるのか？ローレンツ力の大きさはどれくらいか？について説明します。

補足

荷電粒子とは、電荷を持つ粒子のことです。プラスの電荷(電気量\(+q{\mathrm{[C]}}\))を持った粒子とマイナスの電荷(電気量\(-q{\mathrm{[C]}}\))を持った粒子があります。
ローレンツ力は英語では「Lorentz Force」と書きます。
ローレンツ力はオランダの物理学者「ヘンドリック・アントーン・ローレンツ(Hendrik Antoon Lorentz)」により発見されました。

ローレンツ力の向き(フレミングの左手の法則との関係)

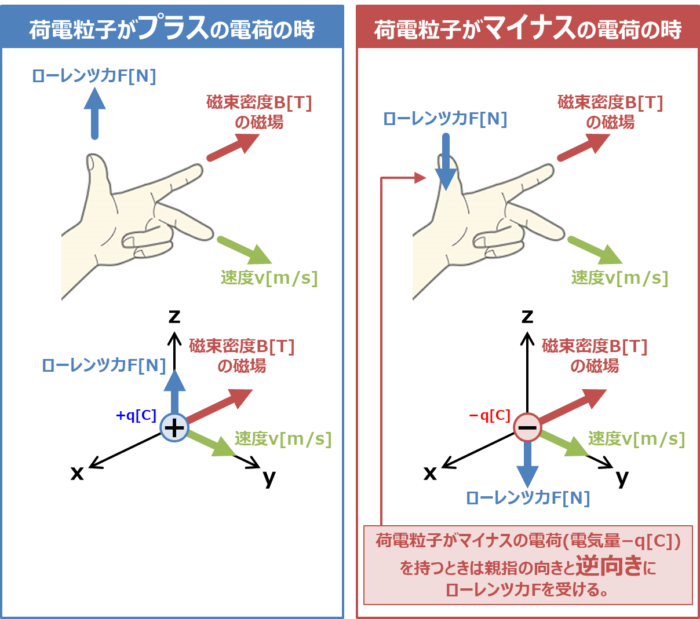
ローレンツ力の向きは左手を使って調べます。

荷電粒子がプラスの電荷(電気量\(+q{\mathrm{[C]}}\))を持つとき、ローレンツ力の向きはフレミングの左手の法則において、

親指

ローレンツ力\(F{\mathrm{[N]}}\)

人差し指

磁束密度\(B{\mathrm{[T]}}\)の磁場

中指

荷電粒子の速度\(v{\mathrm{[m/s]}}\)

となります。

なお、荷電粒子がマイナスの電荷(電気量\(-q{\mathrm{[C]}}\))を持つときは親指の向きと逆向きにローレンツ力\(F\)を受けます。

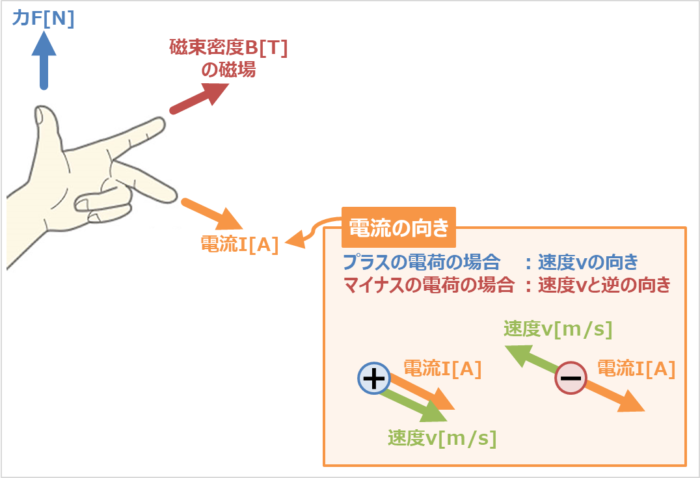
その他の方法としては、「荷電粒子の速度の向き」を「電流の向き」に変換して、フレミングの左手の法則を当てはめる方法があります。この場合、ローレンツ力\(F\)の向きは以下のようになります。

親指

ローレンツ力\(F{\mathrm{[N]}}\)

人差し指

磁束密度\(B{\mathrm{[T]}}\)の磁場

中指

電流\(I{\mathrm{[A]}}\)(プラスの電荷の場合は速度\(v\)の向き、マイナスの電荷の場合は速度\(v\)と逆向きの向き)

ローレンツ力の公式・大きさ

次にローレンツ力の大きさについて説明します。

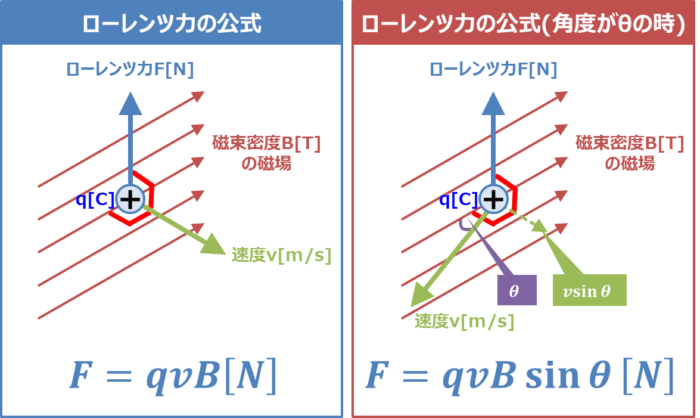
電気量\(+q{\mathrm{[C]}}\)の荷電粒子が速度\(v{\mathrm{[m/s]}}\)で磁束密度\(B{\mathrm{[T]}}\)の磁場中を磁場と垂直な向きで運動している時、荷電粒子に働くローレンツ力\(F{\mathrm{[N]}}\)は次式となります。

ローレンツ力の公式

\begin{eqnarray}
F=qvB{\mathrm{[N]}}\tag{1}
\end{eqnarray}

また、磁場の向きと速度の向きの角度が\({\theta}\)の時、荷電粒子に働くローレンツ力\(F{\mathrm{[N]}}\)は次式となります。

ローレンツ力の公式(角度がθの時)

\begin{eqnarray}
F=qvB{\sin}{\theta}{\mathrm{[N]}}\tag{2}
\end{eqnarray}

上式よりローレンツ力\(F\)は電気量の大きさ\(q\)、速度\(v\)、磁束密度\(B\)に比例することが分かります。

また、角度\({\theta}\)が直角(\({\theta}=90°\))に近いほど\({\sin}{\theta}\)は\(1\)に近づきます。そのため、\({\sin}{\theta}\)は「磁場の向きと速度の向きが直角(\({\theta}=90°\))に近いほどローレンツ力が大きくなるよ！」ということを意味しています。

電荷粒子が磁場と垂直な向きに運動するときは『\({\theta}=90°\)』より『\({\sin}{\theta}=1\)』となるので、(2)式は『\(F=qvB\)』となり、(1)式と同じになります。

ローレンツ力による円運動

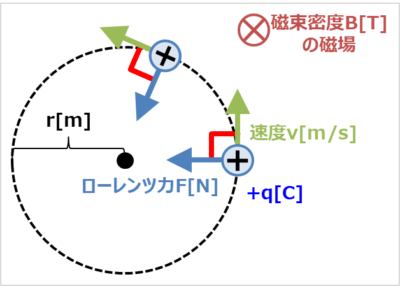
上図に示すように、電気量\(+q{\mathrm{[C]}}\)の荷電粒子が磁束密度\(B{\mathrm{[T]}}\)の一様な磁場中に速度\(v{\mathrm{[m/s]}}\)で飛び込んだ時を考えてみます。なお、磁場の向きは表から裏に向かう向きとします。

この時、荷電粒子はローレンツ力\(F\)を受けて、等速円運動を行います。

この理由について説明します。

フレミングの左手の法則を用いると、速度\(v\)で飛び込んだ荷電粒子は左向きにローレンツ力\(F\)を受け、速度の向きが変わります。

荷電粒子は常に速度の向きと垂直な向きにローレンツ力\(F\)を受けます。そのため、速度の向きが変わると、ローレンツ力の向きも変わります。その結果、以下の流れが繰り返され、円運動を行います。

速度の向きが変わる→ローレンツ力の向きが変わる→速度の向きが変わる→ローレンツ力の向きが変わる→・・・

また、ローレンツ力の向きと速度の向きは常に垂直なので、ローレンツ力は速度の向きを変えるだけであり、荷電粒子の運動エネルギーは変化しません。そのため、荷電粒子の速度は変わらず等速となります。これらの理由により、荷電粒子は等速円運動を行います。

ここで、円の半径を\(r{\mathrm{[m]}}\)とすると、円運動の加速度\(a\)は\(a=\displaystyle\frac{v^2}{r}\)となるため、以下の運動方程式を立てることができます。

\begin{eqnarray}
ma&=&F\\
{\Leftrightarrow}m\frac{v^2}{r}&=&qvB\tag{3}
\end{eqnarray}

(3)式において、左辺を半径\(r\)のみに変形すると、次式となります。

\begin{eqnarray}
r=\frac{mv}{qB}\tag{4}
\end{eqnarray}

また、回転の周期(円を1周回る時間)\(T\)は、半径\(r\)の円周\(2{\pi}r\)、速度\(v\)なので次式となります。

\begin{eqnarray}
T=\frac{2{\pi}r}{v}=\frac{2{\pi}\displaystyle\frac{mv}{qB}}{v}=\frac{2{\pi}m}{qB}\tag{5}
\end{eqnarray}

(4)式より、半径\(r\)の大きさは以下のように変化することが分かります。

質量\(m\)が大きい→半径\(r\)が大きい

質量\(m\)が重いほど、ローレンツ力\(F\)によって速度の向きが変化しにくい。

速度\(v\)が早い→半径\(r\)が大きい
電気量\(q\)が大きい→半径\(r\)が小さい

電気量\(q\)が大きいほど、ローレンツ力\(F=qvB\)が大きくなるため、半径が小さくなる。

磁束密度\(B\)が大きい→半径\(r\)が小さい

磁束密度\(B\)が大きいほど、ローレンツ力\(F=qvB\)が大きくなるため、半径が小さくなる。

また、(5)式より円運動の周期\(T\)は質量\(m\)、電気量\(q\)、磁束密度\(B\)に依存するが、速度\(v\)には依存しないことが分かります。

ローレンツ力と電磁力の関係

次式のローレンツ力\(F_{L}\)と電磁力\(F_{E}\)の関係について説明します。

ローレンツ力と電磁力

\begin{eqnarray}
F_{L}&=&qvB{\mathrm{[N]}}\\
F_{E}&=&IBl{\mathrm{[N]}}
\end{eqnarray}

ローレンツ力\(F_{L}\)は電磁力\(F_{E}\)をミクロの世界でみた時の力となります。そのため、個々の荷電粒子が受けるローレンツ力\(F_{L}\)の総和が電磁力\(F_{E}\)となります。

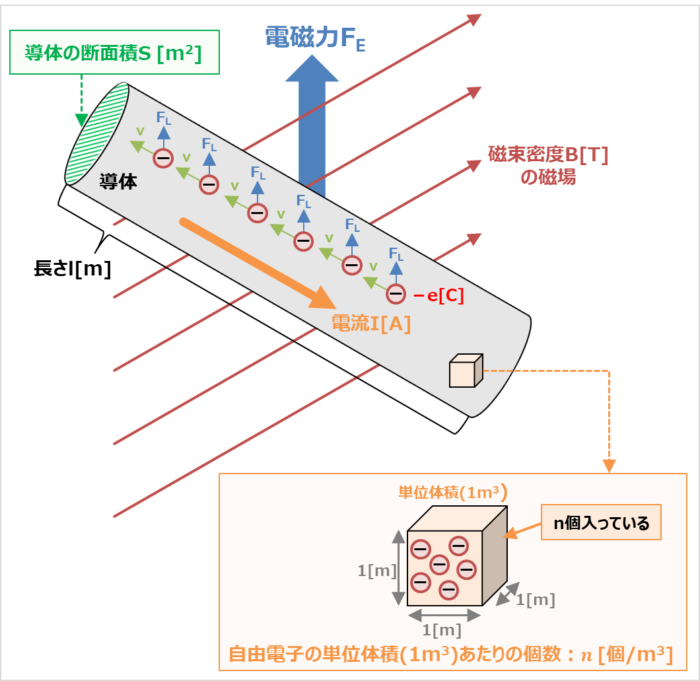
上図のように長さ\(l{\mathrm{[m]}}\)、断面積\(S{\mathrm{[m^2]}}\)の導体が磁束密度\(B{\mathrm{[T]}}\)の磁場中にあるとします。

導体に流れ散る電流の大きさを\(I{\mathrm{[A]}}\)、自由電子1個の電気量を\(-e{\mathrm{[C]}}\)、自由電子の速度を\(v{\mathrm{[m/s]}}\)、自由電子の単位体積(\({\mathrm{m^3}}\))あたりの個数(数密度と呼ばれる)を\(n{\mathrm{[個/m^3]}}\)とし、磁場の向きと導体が垂直であるとします。

この時、自由電子1個が受けるローレンツ力\(F_{L}\)の大きさは次式となります(\(q\)の箇所に\(e\)を代入します)。

\begin{eqnarray}
F_{L}&=&qvB\\
&=&evB{\mathrm{[N]}}\tag{6}
\end{eqnarray}

また、導体の体積\(V\)は次式となります。

\begin{eqnarray}
V=Sl{\mathrm{[m^3]}}\tag{7}
\end{eqnarray}

したがって、導体の中にある自由電子の数\(N\)は次式となります。

\begin{eqnarray}
N&=&n×V\\
&=&n×Sl\\
&=&nSl{\mathrm{[個]}}\tag{8}
\end{eqnarray}

電磁力\(F_{E}\)は導体の中にある自由電子が受けるローレンツ力\(F_{L}\)の総和なので、(6)式と(8)式を用いると、次式となります。

\begin{eqnarray}
F_{E}&=&F_{L}×N\\
&=&evB×nSl\\
&=&envS×Bl\tag{9}
\end{eqnarray}

一方、電流の大きさは『\(I＝envS\)』なので、(9)式は次式に変換することができます。

\begin{eqnarray}
F_{E}&=&envS×Bl\\
&=&IBl{\mathrm{[N]}}\tag{10}
\end{eqnarray}

この流れによって、ローレンツ力\(F_{L}\)から電磁力\(F_{E}\)を導出することができます。