LLCコンバータの設計方法【詳細説明】

この記事ではLLCコンバータの設計方法を詳しく説明します。

仕様

以下に今回設計するLLCコンバータの仕様を示します。この仕様を満たすように設計を進めます。

設計前の準備

【設計準備】LLCコンバータの等価回路

LLCコンバータの設計では、最初にLLCコンバータを簡単な等価回路に変形することから始めます。以下にLLCコンバータを示します。

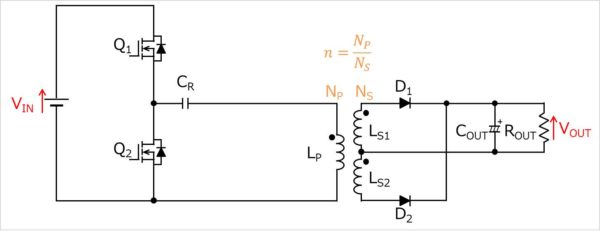
ここで、V_INは入力電圧、Q₁とQ₂はスイッチング素子(上図ではMOSFET)、N_Pは一次巻線の巻数、N_Sは二次巻線の巻数、nは巻数比、C_Rは共振キャパシタンス、L_Rは一次インダクタンス(オープンインダクタンス)、L_S1およびL_S2は二次インダクタンス、D₁とD₂は出力ダイオード、C_OUTは出力コンデンサ、R_OUTは出力抵抗となっています。

漏れインダクタンスと励磁インダクタンスを考慮すると以下の回路となります。

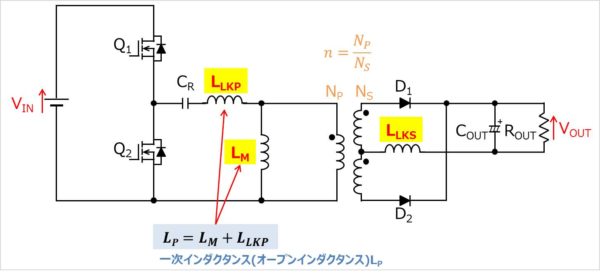
ここで、L_LKPは(一次)漏れインダクタンス、L_Mは励磁インダクタンス、L_LKSは(二次)漏れインダクタンスとなります。一次インダクタンス(オープンインダクタンス)L_Pは二次側トランスをオープンにして測定するインダクタンスのことであり、以下の式で表すことができます。
\begin{eqnarray}
L_{P}= L_{M}+L_{LKP}
\end{eqnarray}
(二次)漏れインダクタンスL_LKSを一次側に換算すると以下の回路となります。

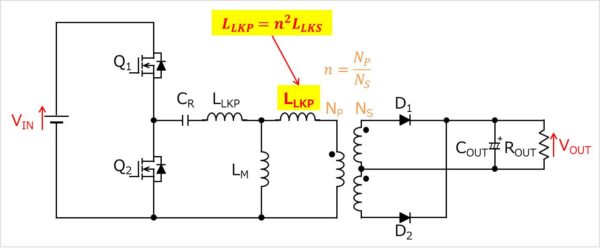
整流回路を交流等価抵抗R_ACに換算すると以下の回路となります。

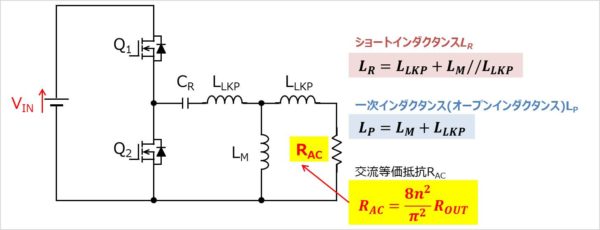
上図の回路において、交流等価抵抗R_ACは以下の式で表すことができます。
\begin{eqnarray}
R_{AC}=\frac{8n^2}{{\pi}^2}R_{OUT}
\end{eqnarray}

また、ショートインダクタンスL_Rは二次側トランスをショートにして測定するインダクタンスのことであり、以下の式で表すことができます。
\begin{eqnarray}
L_{R}= L_{LKP}+L_{M}//L_{LKP}
\end{eqnarray}

LLCコンバータは一般的には上図の等価回路を用いて設計を行います。なお、(二次)漏れインダクタンスL_LKSを考慮していない設計例もあります。

【設計準備】LLCコンバータの共振周波数

LLCコンバータには共振周波数が2つあります。以下に各共振周波数を示します。

• ショートインダクタンスL_Rと共振キャパシタンスC_Rによる共振周波数f₀と共振角周波数ω₀

\begin{eqnarray}
f_{0}=\frac{1}{2{\pi}\sqrt{L_{R}C_{R}}}\\
{\omega}_{0}=2{\pi} f_{0}=\frac{1}{\sqrt{L_{R}C_{R}}}
\end{eqnarray}

• 一次インダクタンス(オープンインダクタンス)L_Pと共振キャパシタンスC_Rによる共振周波数f_Pと共振角周波数ω_P

\begin{eqnarray}
f_{P}=\frac{1}{2{\pi}\sqrt{L_{P}C_{R}}}\\
{\omega}_{P}=2{\pi}f_{P}=\frac{1}{\sqrt{L_{P}C_{R}}}
\end{eqnarray}

【設計準備】伝達関数Mのグラフ

LLCコンバータの設計ではまず伝達関数Mの周波数特性から考えます。LC共振回路の特性インピーダンスZ₀は以下の式で表すことができます。
\begin{eqnarray}
Z_{0}=\sqrt{\displaystyle\frac{L_{R}}{C_{R}}}
\end{eqnarray}
また、Q値は交流等価抵抗R_ACとLC共振回路の特性インピーダンスZ₀の比であり、以下の式で表すことができます。
\begin{eqnarray}
Q=\displaystyle\frac{ Z_{0}}{R_{AC}}=\displaystyle\frac{\sqrt{\displaystyle\frac{L_{R}}{C_{R}}}}{R_{AC}}
\end{eqnarray}
また、ショートインダクタンスL_Rと共振キャパシタンスC_Rによる共振周波数f₀とスイッチング周波数f_SWの比を正規化周波数f_Nと定義します。
\begin{eqnarray}
f_{N}=\frac{f_{SW}}{ f_{0}}
\end{eqnarray}
この場合、LLCコンバータの伝達関数Mは以下の式で表すことができます。

上記の式は基本波近似法(FHA)を用いて近似計算することで求めることができます。

また、上式において、正規化周波数f_Nが変化した時の伝達関数Mをグラフ化すると、以下のように表すことができます。

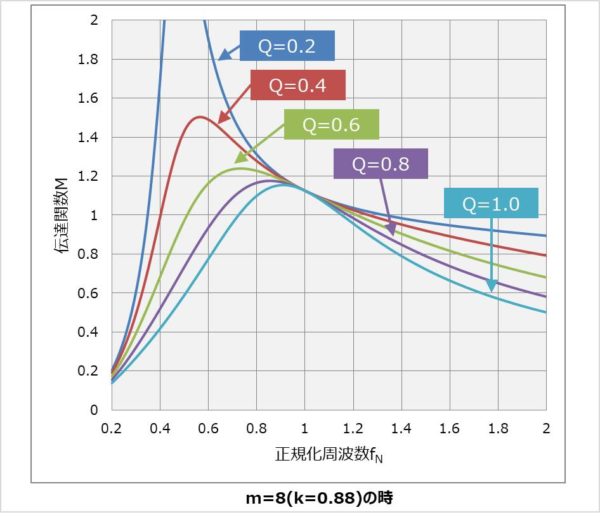
負荷が重くなると、交流等価抵抗R_ACが小さくなるため、Q値が小さくなります。負荷が軽くなると、交流等価抵抗R_ACが大きくなるため、Q値が大きくなります。

Q値の大小によって伝達関数Mのグラフは以下のように変化します。

• Q値が小さいほど、伝達関数Mのピーク値M_PEAKが低域に移動し、かつピーク値M_PEAKが高くなります。
• Q値が大きいほど、伝達関数Mのピーク値M_PEAKが高域に移動し、かつピーク値M_PEAKが低くなります。

また、正規化周波数f_Nが1の時(スイッチング周波数f_SWが共振周波数f₀と等しくなる時)ではQ値が変わっても伝達関数Mの値は変化しません。すなわち、LLCコンバータは共振周波数f₀を基準にして動作していることになります。

ではこれからLLCコンバータの設計方法について説明します。

LLCコンバータの設計

【設計1】励磁インダクタンスL_Mと漏れインダクタンスL_LKPの比ｍを選定する

まず、励磁インダクタンスL_Mと漏れインダクタンスL_LKPのインダクタンス比mを設計します。インダクタンス比mが変化した時における伝達関数Mのグラフを以下に示します(Q=0.31の時)。

インダクタンス比mの値が小さいほど、伝達関数Mのピーク値M_PEAKが高くなりますが、励磁インダクタンスL_Mが小さくなるため、トランスの結合が悪くなり、効率が悪化します。一般的にはインダクタンス比mの値は5～10を選定します。ここでは、mの値を
\begin{eqnarray}
m=\frac{L_{M}}{L_{LKP}}=8
\end{eqnarray}
として設計を進めます。
インダクタンス比mが分かれば、結合係数kを求めることができます。結合係数kは以下の値となります。
\begin{eqnarray}
k=\frac{L_{M}}{L_{P}}=\frac{L_{M}}{L_{M}+L_{LKP}}=\displaystyle \frac{\displaystyle\frac{ L_{M}}{ L_{LKP}}}{\displaystyle\frac{ L_{M}}{ L_{LKP}}+1 }==\frac{m}{m+1}=0.888
\end{eqnarray}

【設計2】伝達関数Mの最小値M_MINを求める

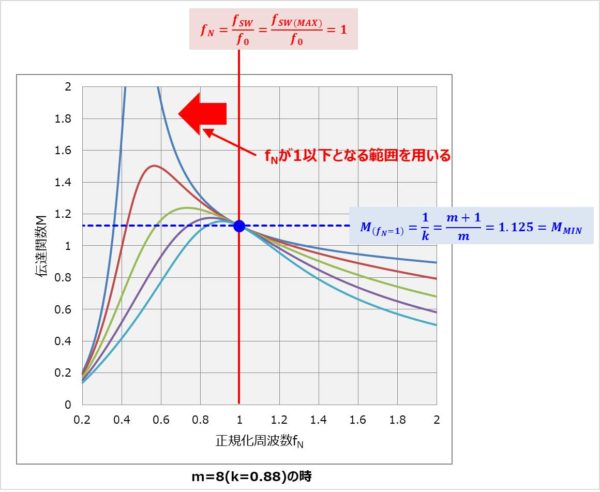
上図の伝達関数Mのグラフにおいて、負荷変動に対して、スイッチング周波数f_SWの変化を最小限にするためには、正規化周波数f_Nが1となる箇所で動作をするのが最適となります。正規化周波数f_Nが1となる時(スイッチング周波数f_SWが共振周波数f₀と等しくなる時)、伝達関数Mは以下の値となります。
\begin{eqnarray}
M_{(f_{N}=1)}=\frac{2n(V_{OUT}+ V_{F})}{V_{IN}}=\displaystyle\frac{1}{\sqrt{\left(\displaystyle\frac{1}{k}\left(1-\displaystyle\frac{1-k^2}{1}\right)\right)^2+\left(\displaystyle\frac{Q}{k}\left(1-\displaystyle\frac{1}{1}\right)\right)^2}}=\frac{1}{k}=\frac{m+1}{m}=1.125
\end{eqnarray}
また、上図の伝達関数Mのグラフにおいて通常用いるのは、正規化周波数f_Nが1以下となる範囲です。そのため、この記事の設計でもスイッチング周波数f_SWは正規化周波数f_Nが1以下となる範囲を用います。

この場合、正規化周波数f_Nが1となる時、スイッチング周波数f_SWが最大スイッチング周波数f_SW(MAX)であり、伝達関数Mが最小値M_MINとなります。

ここで、伝達関数Mの最小値M_MINは、「最大入力電圧V_IN(MAX)=400V」かつ「無負荷」の時において、出力電圧V_OUTを設計値(24V)まで下げられることができるように設定します。すなわち、伝達関数Mの最小値M_MINは以下の値となります。
\begin{eqnarray}
M_{MIN}=M_{(f_{N}=1)}= \frac{2n(V_{OUT}+ V_{F})}{V_{IN(MAX)}}=\frac{1}{k}=\frac{m+1}{m}=1.125
\end{eqnarray}

ここで、ショートインダクタンスL_Rと共振キャパシタンスC_Rによる共振周波数f₀を100[kHz]に設計します。最大スイッチング周波数f_S(MAX)は共振周波数f₀と等しいため100[kHz]となります。

この時、共振角周波数ω₀は以下の値となります。
\begin{eqnarray}
{\omega}_{0}=2{\pi}f_{0}=628318[rad/s]
\end{eqnarray}

以下にインダクタンス比mが5～10の時における結合係数k、伝達関数Mの最小値M_MIN、一次インダクタンスL_Pと励磁インダクタンスL_Mの比を示します。

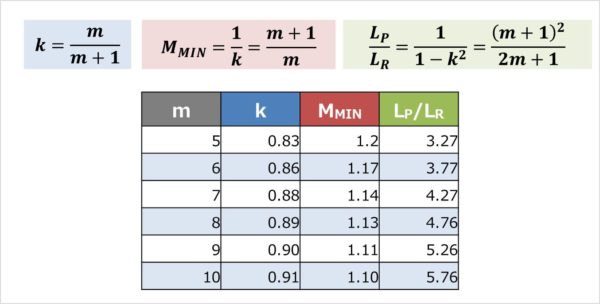
【設計3】巻数比nを求める

巻数比nは以下の式で表すことができます。
\begin{eqnarray}
n=\frac{N_P}{N_S}=\frac{ V_{IN(MAX)}}{2(V_{OUT}+ V_{F})} M_{MIN}=9.146
\end{eqnarray}

【設計4】伝達関数Mの最大値M_MAXを求める

伝達関数Mの最大値M_MAXは、計算した巻数比nにおいて、「最小入力電圧V_IN(MIN)=300V」かつ「定格負荷」の時においても、出力電圧V_OUTを設計値(24V)まで下げられることができるように設定します。
\begin{eqnarray}
M_{MAX}=\frac{2n(V_{OUT}+ V_{F})}{V_{IN(MIN)}}=1.5
\end{eqnarray}

【設計5】伝達関数Mのピーク値M_PEAKを求める

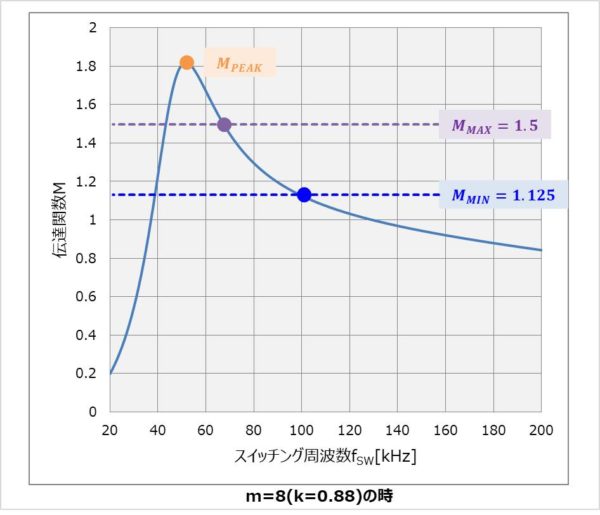
m=8(k=0.88)における伝達関数Mの最小値M_MINと最大値M_MAXを伝達関数Mのグラフにプロットすると上図のようになります。

• 「最大入力電圧V_IN(MAX)=400V」の時には伝達関数MをM_MIN=1.125に下げるためにスイッチング周波数f_SWを上げます。
• 「最小入力電圧V_IN(MIN)=300V」の時には伝達関数MをM_MAX=1.5に上げるためにスイッチング周波数f_SWを下げます。

伝達関数Mのグラフにおいて、伝達関数Mのピーク値M_PEAKの左側の領域で使用することがないように、伝達関数Mのピーク値M_PEAKは伝達関数Mの最大値M_MAXよりも大きくする必要があります。
伝達関数Mのピーク値M_PEAKをM_MAXの20%の余裕を取ると、ピーク値M_PEAKは以下の値となります。
\begin{eqnarray}
M_{PEAK}=1.2 M_{MAX}=1.8
\end{eqnarray}
余裕度は大きい方が良いが、大きくするほど、Q値が小さくなり、共振コンデンサC_Rを大きくする必要があり、損失が増加してしまいます。余裕度の最適値は10%～20%となります。

【設計6】Q値を選定する

伝達関数の式において、Q値と結合係数kを変えた時における伝達関数Mのピーク値M_PEAKをプロットすると、以下のグラフを作成することができます。

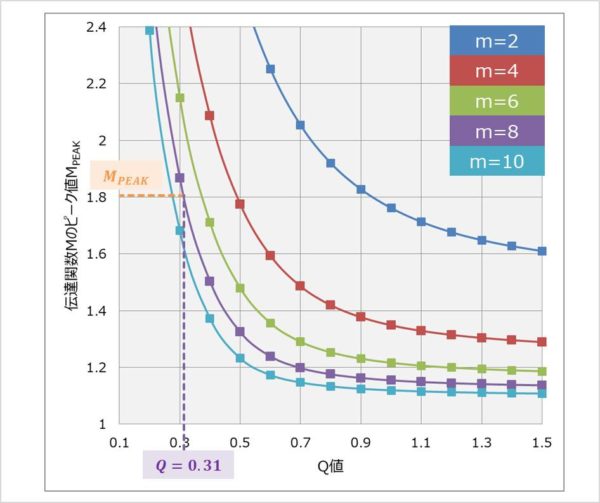
ここで、Q値を0.31付近に設定すれば、mが8の時におけるM_PEAKが1.8になることが分かります。

【設計7】出力抵抗R_OUTと等価直列抵抗R_ACを求める

出力抵抗R_OUTと等価直列抵抗R_ACは以下の式で求めることができます。
\begin{eqnarray}
R_{OUT}=\frac{V_{OUT}}{ I_{OUT}}=4.8[Ω]\\
R_{AC}=\frac{8n^2}{{\pi}^2}R_{OUT}=325.4[Ω]
\end{eqnarray}

【設計8】キャパシタンスとインダクタンスを求める

共振キャパシタンスC_Rは以下の式で求めることができます。
\begin{eqnarray}
C_{R}=\frac{1}{{\omega}_{0} R_{AC}Q}=0.0158[uF]
\end{eqnarray}
上記で求めた共振キャパシタンスC_Rに近い素子値を選定します。今回は共振キャパシタンスC_Rは0.015[uF]としました。

選定した共振キャパシタンスC_RにおいてはQ値は以下の値となります。
\begin{eqnarray}
Q=\frac{1}{{\omega}_{0}C_{R}R_{AC} }=0.326
\end{eqnarray}

ショートインダクタンスL_Rは以下の式で求めることができます。
\begin{eqnarray}
L_{R}=\frac{1}{{{\omega}_{0} }^2 C_{R}}=168.9[uH]
\end{eqnarray}

一次インダクタンス(オープンインダクタンス) L_Pは以下の式で求めることができます。
\begin{eqnarray}
L_{P}=\frac{1}{1-k^2}L_R=\frac{(m+1)^2}{2m+1}L_R=804.6[uH]
\end{eqnarray}

漏れインダクタンスL_LKPと励磁インダクタンスL_M以下の式で求めることができます。
\begin{eqnarray}
L_{LKP}=(1-k) L_{P}=89.4[uH]\\
L_{M}=kL_{M}=715.2[uH]
\end{eqnarray}

一次インダクタンス(オープンインダクタンス) L_Pと共振キャパシタンスC_Rとの共振周波数f_Pは以下の式で求めることができます。
\begin{eqnarray}
f_{P}=\frac{1}{2{\pi}\sqrt{L_{P}C_{R}}}=45.8[kHz]
\end{eqnarray}

結合係数k、Q値、巻数比n、共振周波数f₀の選定が終わったので、以下の式において、スイッチング周波数f_SWを変化させた時の出力電圧V_OUTを求めることができます。グラフにプロットすると以下のようになります。

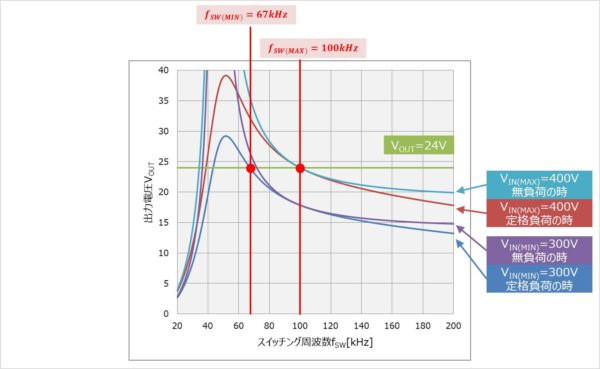
上図のグラフより、スイッチング周波数の最小値f_SW(MIN)は約67kHzになることが分かります。

【設計9】トランスのコアサイズの選定

今回はPC47材のEER28Lのコアを選定しました。EER28Lの実効断面積Aeは81.4[mm²]となります。以下にコアと実効断面積Aeの一覧表を示します。

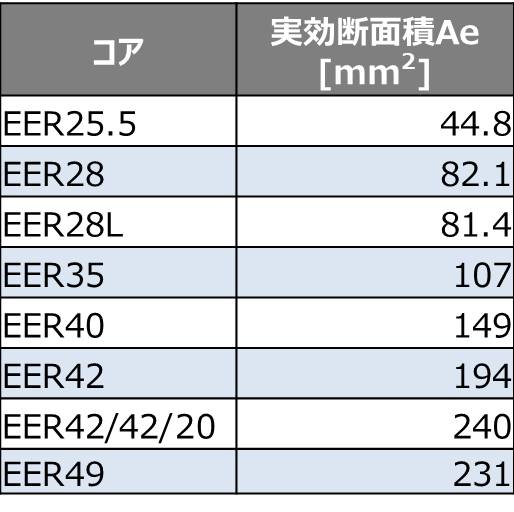
【設計10】選定したコアの磁束密度B_Mの確認

以下にPC47材のBH曲線を示します。ばらつきを含めてコアが飽和しないようにする必要があります。そこで余裕をみると使用する磁束密度B_Mは0.2T以下になるように設計する必要があります。

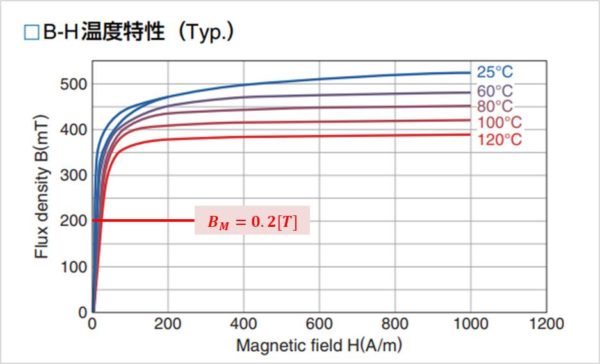
【設計11】トランスの最小一次巻線数N_P(MIN)の導出

LLCコンバータの場合、トランスには正負の電流が流れるため、磁束密度B_Mの2倍がΔBとなります。

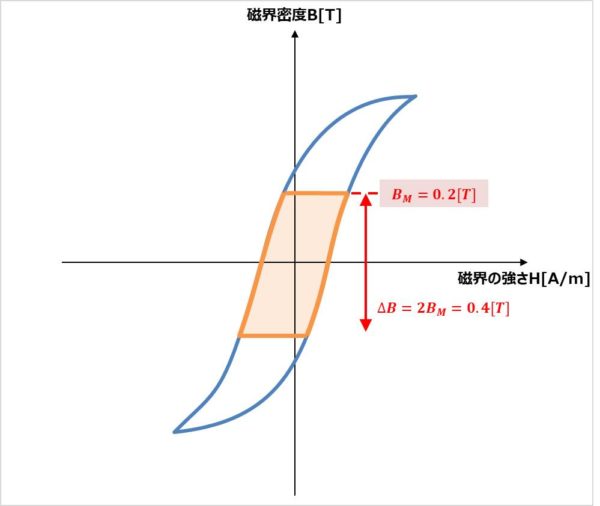
そのため、ΔBは以下の値となります。
\begin{eqnarray}
{\Delta}B=2B_{M}=0.4[T]
\end{eqnarray}
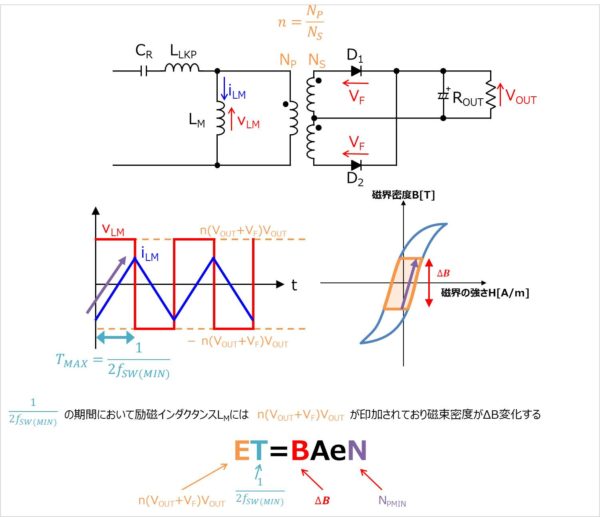
ここで、最小一次巻線数N_P(MIN)は以下の式で求めることができます。
\begin{eqnarray}
N_{P(MIN)}=\frac{n(V_{OUT}+V_{F})}{2f_{SW(MIN)}{\Delta}BAe}=51.1[turns]
\end{eqnarray}
上記で求めた最小一次巻線数N_P(MIN)よりも小さな値にすることで、ΔBの増加を抑えることが出来ます。
また上式はET=BAeNの式を用いることで導出することができます。

【設計12】トランスの二次巻線数N_Sの導出

巻数比nと最小一次巻線数N_P(MIN)が求まったので、二次巻線数N_Sを導出することができます。二次巻線数N_Sは以下の式で求める値よりも大きな値を選定します。
\begin{eqnarray}
N_{S}{>}\frac{N_{P(MIN)}}{n}=5.59[turns]
\end{eqnarray}
したがって、二次巻線数N_Sは6[turns]とします。

【設計13】トランスの一次巻線数N_Pの導出

一次巻線数N_Pは以下の式で求める値よりも大きな値を選定します。
\begin{eqnarray}
N_{P}{>}nN_{S}=54.88[turns]
\end{eqnarray}
したがって、一次巻線数N_Pは55[turns]とします。

選定した一次巻線数N_Pと二次巻線数N_Sより実際の巻数比nは以下の値となります。
\begin{eqnarray}
n=\frac{N_{P}}{N_{S}}=9.17
\end{eqnarray}

【設計14】励磁インダクタに流れる電流i_LMのピーク値I_LM(PEAK)

励磁インダクタに流れる電流i_LMのピーク値I_LM(PEAK)は以下の値となります。
\begin{eqnarray}
I_{LMPEAK}=\frac{n(V_{OUT}+V_{F})}{4L_{M}f_{SW(MIN)}}=1.18[A]
\end{eqnarray}

【設計15】二次巻線に流れる電流i_S

二次巻線に流れる電流i_Sのピーク値I_SPEAKや実行値I_SRMSは正弦波を全波整流した波形と近似して計算を行います。二次巻線に流れる電流i_Sの平均値I_SAVEが出力電流I_OUTと等しくなるため、以下の式で表すことができます。
\begin{eqnarray}
I_{SAVE}= I_{OUT}=5[A]
\end{eqnarray}
そのため、二次巻線に流れる電流i_Sのピーク値I_SPEAKは以下の値となります。
\begin{eqnarray}
I_{SPEAK}=\frac{{\pi} I_{OUT}}{2}=7.85[A]
\end{eqnarray}
二次巻線に流れる電流i_Sの実効値I_SRMSは以下の値となります。
\begin{eqnarray}
I_{SAVE}=\frac{1}{\sqrt{2}} I_{SPEAK}=\frac{{\pi} I_{OUT}}{2\sqrt{2}}=5.55[A]
\end{eqnarray}

【設計16】一次巻線に流れる電流i_P

巻数比nと二次巻線に流れる電流i_Sが分かるので、一次巻線に流れる電流i_Pののピーク値I_PPEAKと実行値I_PRMSを計算することができます。一次巻線に流れる電流i_Pのピーク値I_PPEAKは以下の値となります。
\begin{eqnarray}
I_{PPEAK}=\frac{I_{SPEAK}}{n}=\frac{{\pi}I_{OUT}}{2n}=0.86[A]
\end{eqnarray}
一次巻線に流れる電流流i_Pの実効値I_PRMSは以下の値となります。
\begin{eqnarray}
I_{PRMS}=\frac{I_{SRMS}}{n}=\frac{{\pi} I_{OUT}}{2\sqrt{2}n}=0.61[A]
\end{eqnarray}

【設計17】共振キャパシタC_Rに流れる電流i_R

共振キャパシタC_Rに流れる電流i_Rのピーク値I_RPEAKは以下の値となります。
\begin{eqnarray}
I_{PPEAK}=\sqrt{{I_{LMPEAK}}^2+{I_{PPEAK}}^2}=\sqrt{\left(\frac{n(V_{OUT}+V_{F})}{4L_{M}f_{SW(MIN)}}\right)^2+\left(\frac{{\pi} I_{OUT}}{2n}\right)^2}=1.46[A]
\end{eqnarray}
共振キャパシタC_Rに流れる電流i_Rの実効値I_RRMSは以下の値となります。
\begin{eqnarray}
I_{RRMS}=\frac{1}{\sqrt{2}}I_{RPEAK}=\sqrt{\left(\frac{n(V_{OUT}+V_{F})}{4\sqrt{2}L_{M}f_{SW(MIN)}}\right)^2+\left(\frac{{\pi} I_{OUT}}{2\sqrt{2}n}\right)^2}=1.03[A]
\end{eqnarray}
一次巻線と二次巻線の線径は計算で求めた実効値によって選択します。

【設計18】共振キャパシタC_Rにかかる電圧v_C

共振キャパシタC_Rにかかる電圧v_Cのピーク値V_CPEAKは以下の値となります。
\begin{eqnarray}
V_{CPEAK}=\frac{V_{IN(MAX)}}{2}+\frac{I_{RPEAK}}{2{\pi}f_{0}C_{R}}=346.8[V]
\end{eqnarray}
入力電圧が最大値V_IN(MAX)の時には、共振キャパシタC_Rに流れる電流i_Cはピーク値I_PPEAKまで達しないため、実際にはここまでピーク値は大きくなりません。

シミュレーションで動作確認

LTspiceを用いて設計値において正常に動作をするか確認してみます。
設計値を求めた後にシミュレーションで動作確認を行うと、電流電圧波形からピーク値等が計算できますし、設計に間違いがないかを確認することができます。以下に今回のパラメータにおけるシミュレーション結果を示します。

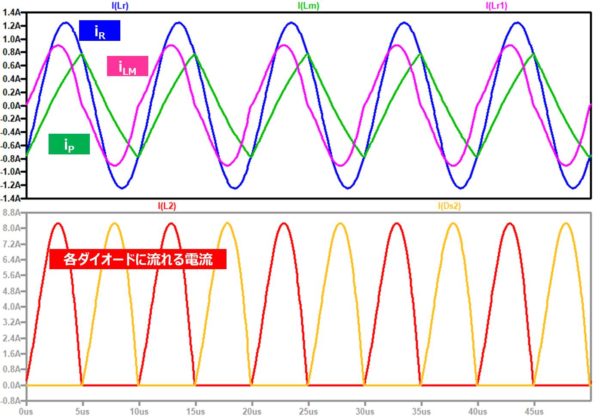
シミュレーションモデルは以下のようになっています。

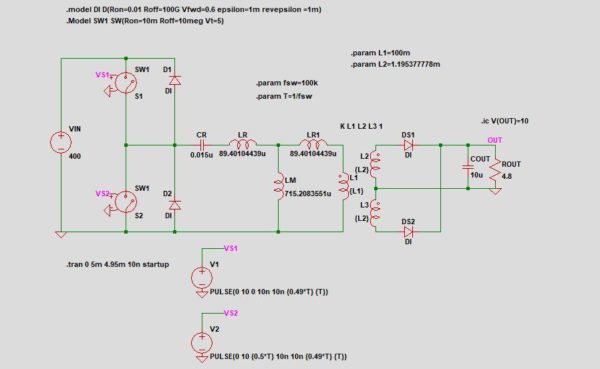
まとめ

この記事ではLLCコンバータについて、以下の内容を説明しました。

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。

全記事一覧