この記事では『キルヒホッフの法則』について
- キルヒホッフの法則(第1法則・第2法則)とは
- キルヒホッフの第1法則の説明
- キルヒホッフの第2法則の説明
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
キルヒホッフの法則とは
キルヒホッフの法則は、すべての電気回路で使用することのできる万能の法則です。
キルヒホッフの法則には「第1法則」と「第2法則」があります。
後ほど各法則について詳しく説明しますが、簡単にまとめると下記のようになります。
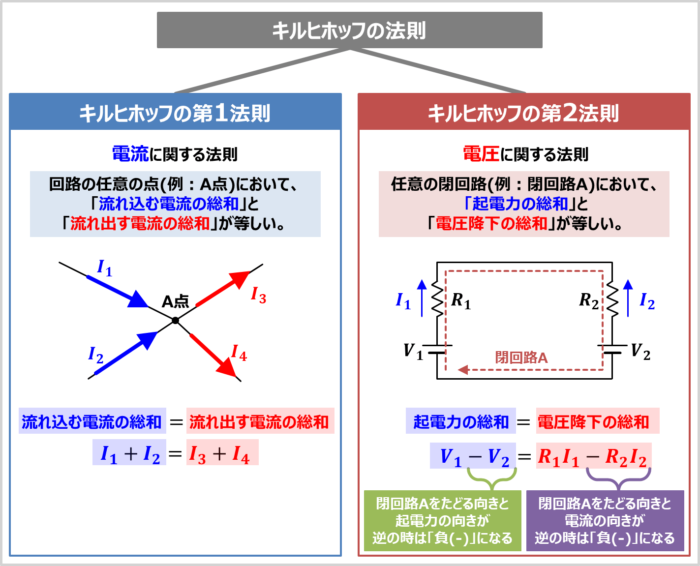
キルヒホッフの第1法則
電流に関する法則です。
回路の任意の点(上図の場合はA点)において、「流れ込む電流の総和」と「流れ出す電流の総和」が等しい。
キルヒホッフの第2法則
電圧に関する法則です。
任意の閉回路(上図の場合は閉回路A)において、「起電力の総和」と「電圧降下の総和」が等しい。
ではこれから「キルヒホッフの第1法則」と「キルヒホッフの第2法則」について個別に説明していきます(キルヒホッフの法則を用いる際の注意点なども詳しく説明します)。
キルヒホッフの第1法則
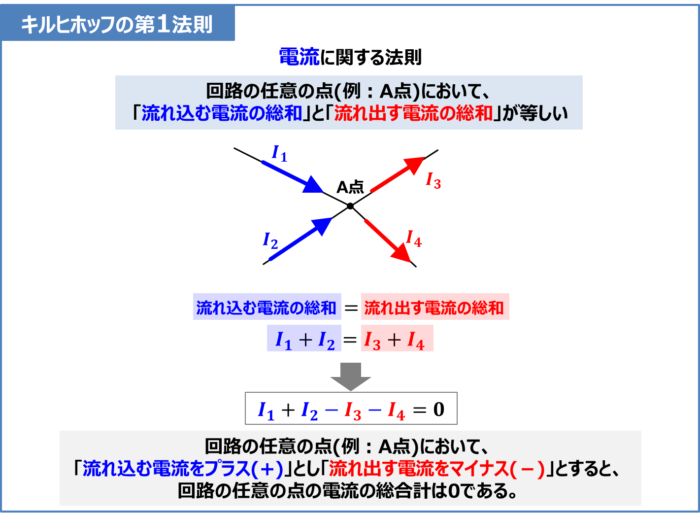
キルヒホッフの第1法則は電流に関する法則です。
キルヒホッフの第1法則
回路の任意の点(上図の場合はA点)において、「流れ込む電流の総和」と「流れ出す電流の総和」が等しい。
例えば、上図のように、「A点に流れ込んでいる電流が\(I_1\)と\(I_2\)」で「A点から流れ出している電流が\(I_3\)と\(I_4\)」の場合、キルヒホッフの第1法則より、次式が成り立ちます。
\begin{eqnarray}
\mbox{A点に流れ込む電流の総和}&=&\mbox{A点から流れ出す電流の総和}\\
\\
{\Leftrightarrow}I_1+I_2&=&I_3+I_4\tag{1-1}
\end{eqnarray}
ここで、(1-1)式を変形してみます。(1-1)式の右辺を左辺に移行すると、次式が成り立ちます。
\begin{eqnarray}
I_1+I_2-I_3-I_4=0\tag{1-2}
\end{eqnarray}
(1-2)式より、キルヒホッフの第1法則は、以下のように言い換えることもできます。
回路の任意の点(上図の場合はA点)において、「流れ込む電流をプラス(+)」とし「流れ出す電流をマイナス(-)」とすると、回路の任意の点(上図の場合はA点)の電流の総合計は0である。
【キルヒホッフの第1法則】電流の向きが分からない時にはどうするか?
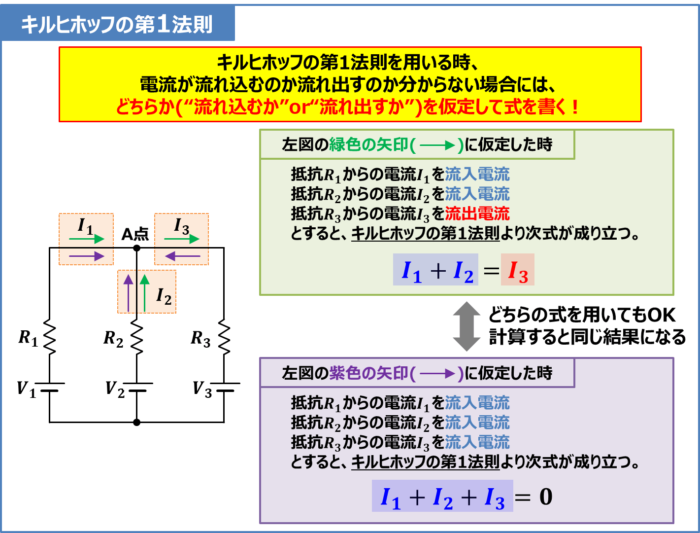
キルヒホッフの第1法則を用いる時、複雑な回路だと、回路の任意の点において、電流が流れ込むのか流れ出すのか分からない場合があります。
この場合、どちらか("流れ込むか"or"流れ出すか")を仮定して式を書きます。
例えば、上図のような回路において、A点への電流の向きが分からなかった場合を考えてみましょう。
抵抗\(R_1\)からの電流\(I_1\)を流入電流、抵抗\(R_2\)からの電流\(I_2\)を流入電流、抵抗\(R_3\)からの電流\(I_3\)を流出電流と仮定すると、キルヒホッフの第1法則より次式が成り立ちます。
\begin{eqnarray}
\mbox{A点に流れ込む電流の総和}&=&\mbox{A点から流れ出す電流の総和}\\
\\
{\Leftrightarrow}
I_1+I_2&=&I_3\tag{1-3}
\end{eqnarray}
抵抗\(R_1\)からの電流\(I_1\)を流入電流、抵抗\(R_2\)からの電流\(I_2\)を流入電流、抵抗\(R_3\)からの電流\(I_3\)を流入電流と仮定すると、キルヒホッフの第1法則より次式が成り立ちます。
\begin{eqnarray}
\mbox{A点に流れ込む電流の総和}&=&\mbox{A点から流れ出す電流の総和}\\
\\
{\Leftrightarrow}
I_1+I_2+I_3&=&0\tag{1-4}
\end{eqnarray}
キルヒホッフの第1法則を用いる時、(1-3)式を用いても(1-4)式を用いてもOKです。計算した結果、マイナス(-)の値となったら、仮定した電流の向きの方向と「逆向き」の電流が流れているということになります。
例えば、(1-4)式では、抵抗\(R_3\)からの電流\(I_3\)を流入電流と仮定して計算していますが、計算した結果、電流\(I_3\)の値がマイナス(-)の値になったら、抵抗\(R_3\)からの電流\(I_3\)はA点からの流出電流であるということになります。
流入電流と流出電流について
流入電流は「任意の点に流れ込む電流」、流出電流は「任意の点から流れ出す電流」のことを指します。
キルヒホッフの第2法則
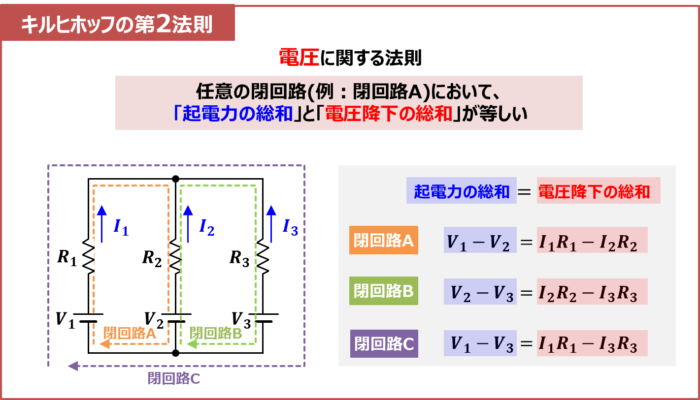
キルヒホッフの第2法則は電圧に関する法則です。
キルヒホッフの第2法則
任意の閉回路(上図の場合は閉回路A)において、「起電力の総和」と「電圧降下の総和」が等しい。
例えば、上図に示す回路において、閉回路A(オレンジ色の閉回路)に関してキルヒホッフの第2法則を用いて式を導出すると、次式となります。
\begin{eqnarray}
\mbox{起電力の総和}&=&\mbox{電圧降下の総和}\\
\\
V_1-V_2&=&I_1R_1-I_2R_2\tag{2-1}
\end{eqnarray}
(2-1)式をキルヒホッフの第2法則を用いて式を導出する手順は下記となります。
手順
- 閉回路をたどる向きを決める
- 各抵抗に流れる電流の向きを仮に決める
- 起電力の総和を求める
- 電圧降下の総和を求める
- 「キルヒホッフの第2法則」に当てはめる
ではこれから、各手順について順番に説明していきます。
【STEP1】閉回路をたどる向きを決める
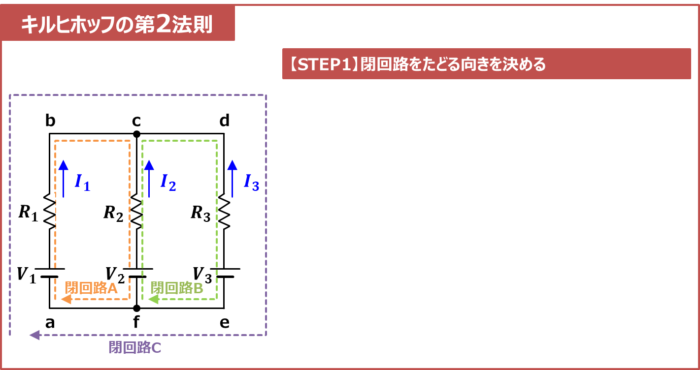
まず、閉回路をたどる向きを決めます。閉回路をたどる方向は自由に設定して頂いてOKです。今回は、時計回りの向きに閉回路Aをたどりましょう。
閉回路とは
閉回路は、回路の任意の出発点から、任意の経路を通って、出発点に戻る一巡の回路のことを指します。例えば、上図に示す回路の場合、閉回路は3つあります。
- 閉回路A
- a点を出発点とし、「a→b→c→f→a」と一巡したものが閉回路Aとなります。
- 閉回路B
- f点を出発点とし、「f→c→d→e→f」と一巡したものが閉回路Bとなります。
- 閉回路C
- a点を出発点とし、「a→b→c→d→e→f→a」と一巡したものが閉回路Cとなります。
【STEP2】各抵抗に流れる電流の向きを仮に決める
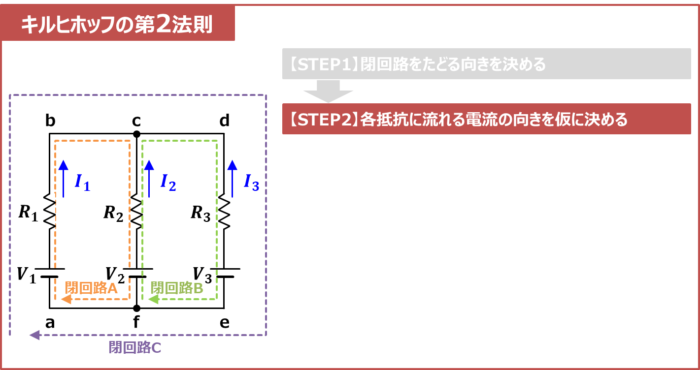
次に、各抵抗に流れる電流の向きを仮に決めます。今回は、上図に示すような向きに電流\(I_1\)~\(I_3\)を決めました。
【STEP3】起電力の総和を求める
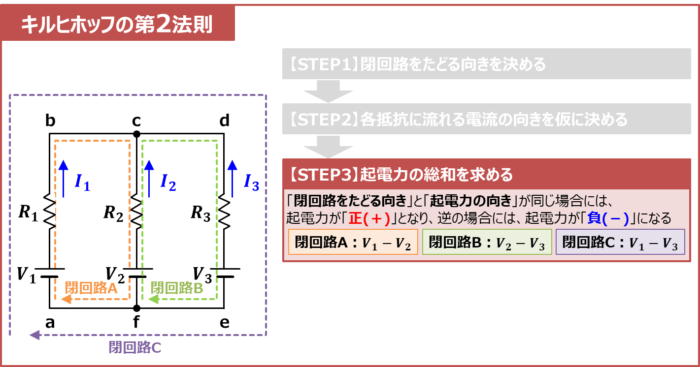
次に、起電力の総和を求めます。上図に示す回路の場合、起電力は電源電圧のことを指しています。
閉回路Aの経路を見ると、電源が2つあります(\(V_1\)と\(V_2\))。ここで注意点があります。
注意点
起電力の総和を単に足し算して「\(V_1+V_2\)」としてはいけません。
電源電圧(起電力)の総和を求める際、起電力の極性(正or負)を考える必要があります。
【STEP1】において決めた「閉回路をたどる向き」と「起電力の向き」が同じ場合には、起電力が「正(+)」となり、逆の場合には、起電力が「負(-)」となります。
上図に示す回路において、閉回路Aを見ると、電源電圧\(V_1\)は「閉回路をたどる向き」と同じなので「正(+)」、電源電圧\(V_2\)は「閉回路をたどる向き」と逆なので「負(-)」となります。そのため、起電力の総和は次式となります。
\begin{eqnarray}
\mbox{起電力の総和}=V_1-V_2\tag{2-2}
\end{eqnarray}
【STEP4】電圧降下の総和を求める
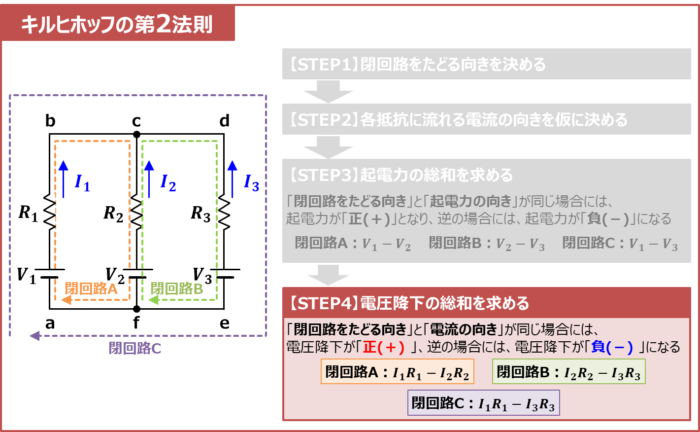
閉回路Aにおいて、電圧降下は2つあります(「抵抗\(R_1\)による電圧降下\(I_1R_1\)」と「抵抗\(R_2\)による電圧降下\(I_2R_2\)」)。ここでも注意点があります。
注意点
電圧降下の総和を単に足し算して「\(I_1R_1+I_2R_2\)」としてはいけません。
電圧降下の総和を求める際、電圧降下の向き(正or負)を考える必要があります。
【STEP1】において決めた「閉回路をたどる向き」と【STEP2】で決めた「電流の向き」が同じ場合には、電圧降下が「正(+)」、逆の場合には、電圧降下が「負(-)」となります。
に示す回路において、閉回路Aを見ると、電流\(I_1\)は「閉回路をたどる向き」と同じなので「抵抗\(R_1\)による電圧降下\(I_1R_1\)」は「正(+)」、電流\(I_2\)は「閉回路をたどる向き」と逆なので「抵抗\(R_2\)による電圧降下\(I_2R_2\)」は「負(-)」となります。そのため、電圧降下の総和は次式となります。
\begin{eqnarray}
\mbox{電圧降下の総和}=I_1R_1-I_2R_2\tag{2-3}
\end{eqnarray}
【STEP5】「キルヒホッフの第2法則」に当てはめる
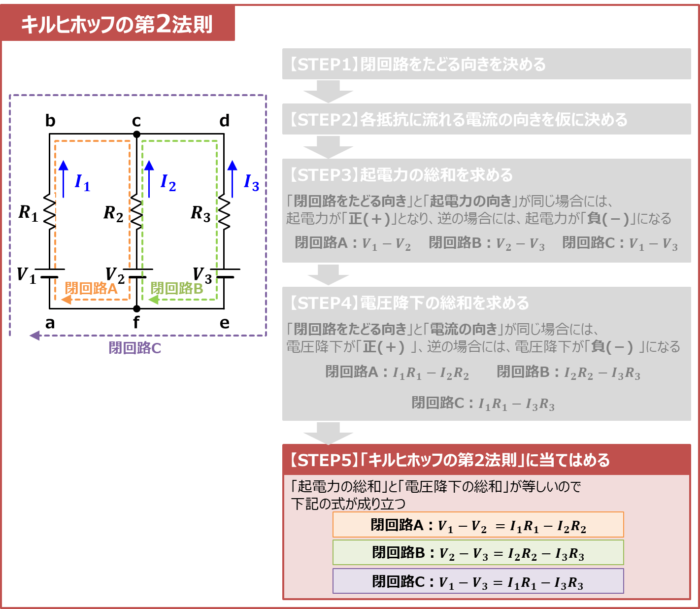
キルヒホッフの第2法則は、任意の閉回路において、「起電力の総和」と「電圧降下の総和」が等しいという法則でした。これは、【STEP3】で求めた「起電力の総和」と【STEP4】で求めた「電圧降下の総和」が等しいということを言っています。
すなわち、(2-2)式と(2-3)式が等しいということなので次式が成り立ちます。
\begin{eqnarray}
\mbox{起電力の総和}&=&\mbox{電圧降下の総和}\\
\\
{\Leftrightarrow}V_1-V_2&=&I_1R_1-I_2R_2\tag{2-4}
\end{eqnarray}
上式は閉回路Aに焦点を当てた時の式です。閉回路Bと閉回路Cについても同様の手順で式を導出することができます。
あわせて読みたい
これで「キルヒホッフの第1法則」と「キルヒホッフの第2法則」の説明は終わりです。
『キルヒホッフの法則を用いた例題』については下記の記事で別途詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。 続きを見る
キルヒホッフの法則(第1法則・第2法則)の例題
まとめ
この記事では『キルヒホッフの法則』について、以下の内容を説明しました。
- キルヒホッフの法則(第1法則・第2法則)とは
- キルヒホッフの第1法則の説明
- キルヒホッフの第2法則の説明
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






