【インピーダンスマッチングとは】『計算方法』などを分かりやすく解説！

この記事ではインピーダンスマッチングについて

インピーダンスマッチングとは
インピーダンスマッチングの計算

などを図を用いて分かりやすく説明しています。

インピーダンスマッチングとは

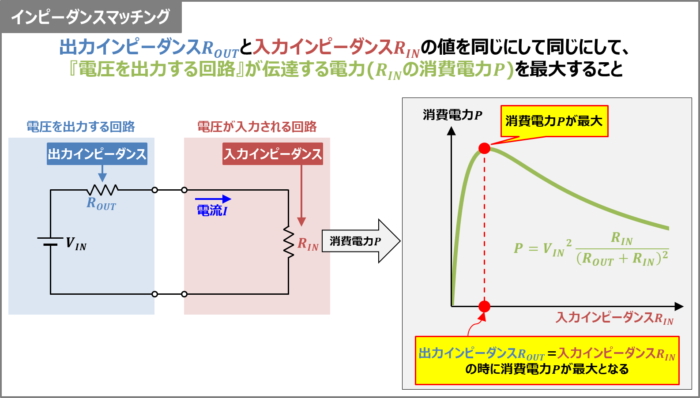
インピーダンスマッチングとは『電圧を出力する回路』の出力インピーダンス\(R_{OUT}\)と『電圧が入力される回路(負荷側)』の入力インピーダンス\(R_{IN}\)の値を同じにすることです。

出力インピーダンス\(R_{OUT}\)と入力インピーダンス\(R_{IN}\)を同じにすることで、『電圧を出力する回路』が伝達する電力を最大にすることができます。

インピーダンスマッチングはインピーダンス整合とも呼ばれています。

もう少し詳しく

このインピーダンスマッチングについて式を用いて詳しく説明します。なお、この記事では分かりやすく説明するため、『電圧を出力する回路』の電圧源は直流電圧源、インピーダンスは単純な抵抗として考えています。

上図において、\(V_{IN}\)は直流電圧源の電圧、\(R_{OUT}\)は出力インピーダンス、\(R_{IN}\)は入力インピーダンスを示しています。

この時、回路を流れる電流\(I\)はオームの法則より次式となります。

\begin{eqnarray}
I=\frac{V_{IN}}{R_{OUT}+R_{IN}}\tag{1}
\end{eqnarray}

したがって、入力インピーダンス\(R_{IN}\)の両端電圧は「抵抗×電流」より次式となります。

\begin{eqnarray}
V=R_{IN}×I=R_{IN}\frac{V_{IN}}{R_{OUT}+R_{IN}}\tag{2}
\end{eqnarray}

ゆえに、入力インピーダンス\(R_{IN}\)で消費される電力\(P\)は「電圧×電流」より次式となります。

\begin{eqnarray}
P=VI=R_{IN}×I={V_{IN}}^2\frac{{R_{IN}}}{(R_{OUT}+R_{IN})^2}\tag{3}
\end{eqnarray}

ここで、直流電圧源の電圧\(V_{IN}\)を\(50{\mathrm{[V]}}\)、出力インピーダンス\(R_{OUT}\)を\(50{\mathrm{[Ω]}}\)とした時において、入力インピーダンス\(R_{IN}\)を変えた時の消費電力\(P\)を下図に示します。消費電力\(P\)が最大になるのは、入力インピーダンス\(R_{IN}\)が\(50{\mathrm{[Ω]}}\)の時(出力インピーダンス\(R_{OUT}\)と同じ時)となります。

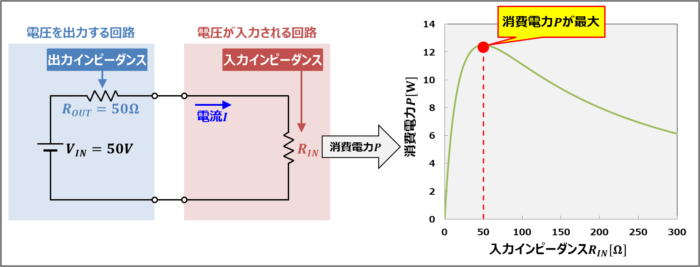
また、出力インピーダンス\(R_{OUT}\)に流れる電流と入力インピーダンス\(R_{IN}\)に流れる電流は同じなので、マッチングしている時(\(R_{OUT}\)=\(R_{IN}\)の時)は出力インピーダンス\(R_{OUT}\)での消費電力と入力インピーダンス\(R_{IN}\)での消費電力は等しくなります。

ポイント

このように、出力インピーダンス\(R_{OUT}\)と入力インピーダンス\(R_{IN}\)の値を同じにして、『電圧が出力される回路』が伝達する電力を最大すること(言い換えれば、『電圧が入力される回路』の消費電力を最大にすること)をインピーダンスマッチング(インピーダンス整合)と呼びます。

補足

グラフより、入力インピーダンス\(R_{IN}\)が出力インピーダンス\(R_{OUT}\)より小さくなると、急激に消費電力が低下します(\(50{\mathrm{[Ω]}}\)より下の領域)。そのため、入力インピーダンス\(R_{IN}\)が出力インピーダンス\(R_{OUT}\)より少し大きめになるように調整することで、部品がバラついた時でも消費電力の低下を抑えることができます。

インピーダンスマッチングの計算

入力インピーダンス\(R_{IN}\)を変えた時の消費電力\(P\)をプロットすると、消費電力\(P\)が最大になる箇所では、出力インピーダンス\(R_{OUT}\)と入力インピーダンス\(R_{IN}\)の値が同じになることを説明しました。

なお、グラフ上にプロットしなくても、(3)式から消費電力\(P\)が最大になる条件を求めることができます。

消費電力が最大となる箇所では曲線の傾きがゼロとなります。すなわち、(3)式を微分した値がゼロの時が消費電力が最大となる条件です。(3)式は以下の式に変形することができます。

\begin{eqnarray}
P={V_{IN}}^2\frac{{R_{IN}}}{(R_{OUT}+R_{IN})^2}={V_{IN}}^2{R_{IN}}(R_{OUT}+R_{IN})^{-2}
\end{eqnarray}

上式を\(R_{IN}\)で微分すると次式となります。

\begin{eqnarray}
\frac{dP}{dR_{IN}}&=&\frac{d}{dR_{IN}}\left[{V_{IN}}^2{R_{IN}}(R_{OUT}+R_{IN})^{-2}\right]\\
&=&{V_{IN}}^2\frac{d}{dR_{IN}}\left[{R_{IN}}(R_{OUT}+R_{IN})^{-2}\right]\\
&=&{V_{IN}}^2\left[1×(R_{OUT}+R_{IN})^{-2}+{R_{IN}}×-2(R_{OUT}+R_{IN})^{-3}\right]\\
&=&-{V_{IN}}^2\frac{{R_{IN}}-{R_{OUT}}}{(R_{OUT}+R_{IN})^3}\tag{4}
\end{eqnarray}

(4)式がゼロになるときは『\(R_{IN}=R_{OUT}\)』の時であることが分かります。