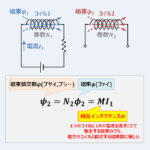
この記事では相互インダクタンスに関する様々な例題を解いています。
なお、相互インダクタンスについては下記の記事に詳しく説明しています。例題を解く前に以下の記事も参考にしていただければ幸いです。
-

【相互インダクタンスとは】『単位』や『例題』などを解説!
続きを見る
【例題1】『無限長ソレノイド』と『その外側に巻かれたコイル』との間の相互インダクタンス(その1)
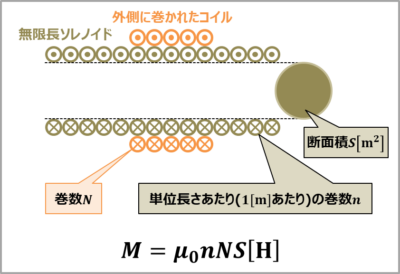

例題1
上図に示すように、単位長さあたり(\(1{\mathrm{[m]}}\)あたり)の巻数が\(n\)、断面積が\(S{\mathrm{[m^2]}}\)の『無限長ソレノイドコイル』の外側に巻数\(N\)のコイルが巻かれている時の両コイル間の相互インダクタンス\(M\)を求めてみましょう。
解答
ポイント
相互インダクタンス\(M\)を求めるためには、『無限長ソレノイドコイル』に電流\(I_1\)を流した時において、『外側に巻かれたコイル』と鎖交する磁束数\({\psi}_2\)を求めます。
『無限長ソレノイドコイル』に電流\(I_1{\mathrm{[A]}}\)が流れている時、ソレノイド内部の磁界\(H{\mathrm{[A/m]}}\)は次式となります。
\begin{eqnarray}
H=nI_1{\mathrm{[A/m]}}\tag{1-1}
\end{eqnarray}
そのため、磁束密度\(B{\mathrm{[T]}}\)は真空の透磁率\({\mu}_0=4{\pi}×10^{-7}\)を用いると、次式となります。
\begin{eqnarray}
B={\mu}_0H={\mu}_0nI_1{\mathrm{[T]}}\tag{1-2}
\end{eqnarray}
『外側に巻かれたコイル』の断面\(S\)と交わる磁束\({\phi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
{\phi}_2=BS={\mu}_0nI_1S{\mathrm{[wb]}}\tag{1-3}
\end{eqnarray}
したがって、『外側に巻かれたコイル』の巻数は\(N\)なので、磁束鎖交数\({\psi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
{\psi}_2=N{\phi}_2={\mu}_0nNI_1S{\mathrm{[wb]}}\tag{1-4}
\end{eqnarray}
『無限長ソレノイドコイル』に流れている電流\(I_1\)、『外側に巻かれたコイル』の磁束鎖交数\({\psi}_2\)、相互インダクタンス\(M\)の関係は『\({\psi}_2=MI_1\)』なので、『無限長ソレノイドコイル』と『その外側に巻かれたコイル』との間の相互インダクタンス\(M\)は次式となります。
\begin{eqnarray}
M=\frac{{\psi}_2}{I_1}=\frac{{\mu}_0nNI_1S}{I_1}={\mu}_0nNS=4{\pi}nNS×10^{-7}{\mathrm{[H]}}\tag{1-5}
\end{eqnarray}
【例題2】『円筒ソレノイド』と『その外側に巻かれたコイル』との間の相互インダクタンス(その2)
例題2
上図に示すように、単位長さあたり(\(1{\mathrm{[m]}}\)あたり)の巻数が\(n=500\)、断面積が\(S=0.5{\mathrm{[m^2]}}\)の無限長ソレノイドコイルの外側に巻数\(N=200\)のコイルが巻かれている時の両コイル間の相互インダクタンス\(M\)を求めてみましょう。
解答
『円筒ソレノイド』と『その外側に巻かれたコイル』との間の相互インダクタンス\(M\)は(1-5)式を用いると以下の値となります。
\begin{eqnarray}
M&=&4{\pi}nNS×10^{-7}\\
&=&4{\pi}×200×500×0.5×10^{-7}\\
&=&0.628{\mathrm{[H]}}\tag{2-1}
\end{eqnarray}
【例題3】『無限長の導線』と『導線から距離dの箇所にあるN巻の長方形コイル』との間の相互インダクタンス
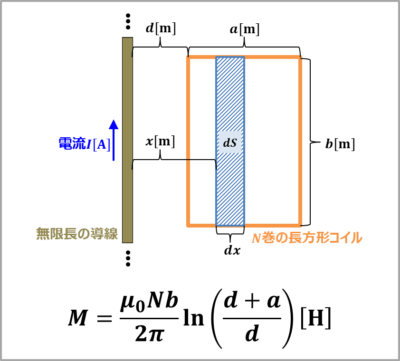

例題3
上図に示すように、『無限長の導線』と平行に距離\(d{\mathrm{[m]}}\)離れて、『同一平面に置かれた巻数\(N\)の長方形コイル(\(a×b{\mathrm{[m^2]}}\))』がある。この時の両コイル間の相互インダクタンス\(M\)を求めてみましょう。
解答
ポイント
相互インダクタンス\(M\)を求めるためには、『無限長の導線』に電流\(I_1\)を流した時において、『同一平面に置かれた巻数\(N\)の長方形コイル』と鎖交する磁束数\({\psi}_2\)を求めます。
『無限長の導線』に電流\(I_1{\mathrm{[A]}}\)が流れている時、距離\(x\)における磁界\(H{\mathrm{[A/m]}}\)は次式となります。
\begin{eqnarray}
H=\frac{I_1}{2{\pi}x}{\mathrm{[A/m]}}\tag{3-1}
\end{eqnarray}
そのため、磁束密度\(B{\mathrm{[T]}}\)は真空の透磁率\({\mu}_0=4{\pi}×10^{-7}\)を用いると、次式となります。
\begin{eqnarray}
B={\mu}_0H=\frac{{\mu}_0I_1}{2{\pi}x}{\mathrm{[T]}}\tag{3-2}
\end{eqnarray}
『長方形コイル』において、幅\(dx\)、長さ\(b\)の部分と交わる磁束\(d{\phi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
d{\phi}_2=B×dS=B×bdx=\frac{{\mu}_0I_1}{2{\pi}x}bdx{\mathrm{[wb]}}\tag{3-3}
\end{eqnarray}
したがって、『長方形コイル』の全体と鎖交する磁束\({\phi}_2\)は次式となります。
\begin{eqnarray}
{\phi}_2&=&{\displaystyle\int}_{d}^{d+a}d{\phi}_2\\
&=&{\displaystyle\int}_{d}^{d+a}\frac{{\mu}_0I_1}{2{\pi}x}bdx\\
&=&\frac{{\mu}_0I_1b}{2{\pi}}{\displaystyle\int}_{d}^{d+a}\frac{1}{x}dx\\
&=&\frac{{\mu}_0I_1b}{2{\pi}}{\ln}\left(\frac{d+a}{d}\right){\mathrm{[wb]}}\tag{3-4}
\end{eqnarray}
『長方形コイル』の巻数は\(N\)なので、磁束鎖交数\({\psi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
{\psi}_2=N{\phi}_2=\frac{{\mu}_0NI_1b}{2{\pi}}{\ln}\left(\frac{d+a}{d}\right){\mathrm{[wb]}}\tag{3-5}
\end{eqnarray}
『無限長の導線』に流れている電流\(I_1\)、『長方形コイル』の磁束鎖交数\({\psi}_2\)、相互インダクタンス\(M\)の関係は『\({\psi}_2=MI_1\)』なので、『無限長の導線』と『導線から距離\(d\)の箇所にある\(N\)巻の長方形コイル』との間の相互インダクタンス\(M\)は次式となります。
\begin{eqnarray}
M=\frac{{\psi}_2}{I_1}=\frac{{\mu}_0Nb}{2{\pi}}{\ln}\left(\frac{d+a}{d}\right){\mathrm{[H]}}\tag{3-6}
\end{eqnarray}
【例題4】『円形コイル』と『円筒ソレノイド』との間の相互インダクタンス
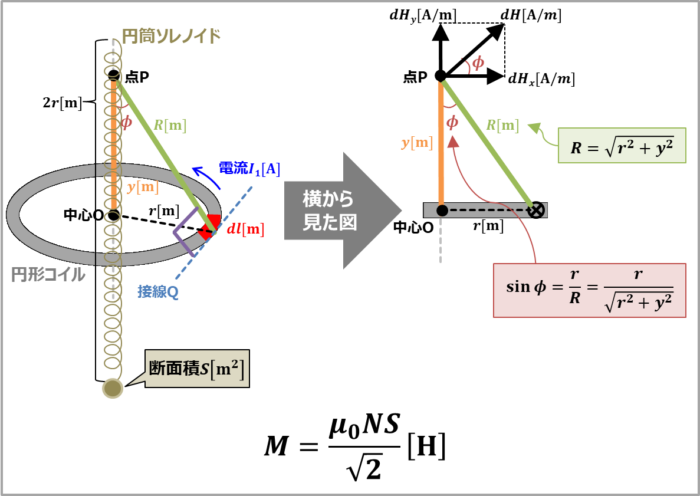

例題4
上図に示すように、半径\(r{\mathrm{[m]}}\)の『円形コイル』の中心に長さ\(2r{\mathrm{[m]}}\)、単位長さあたり(\(1{\mathrm{[m]}}\)あたり)の巻数が\(n\)、断面積が\(S{\mathrm{[m^2]}}\)の『円筒ソレノイドコイル』がある。この時の両コイル間の相互インダクタンス\(M\)を求めてみましょう。
解答
ポイント
相互インダクタンス\(M\)を求めるためには、『円形コイル』に電流\(I_1\)を流した時において、『円筒ソレノイドコイル』と鎖交する磁束数\({\psi}_2\)を求めます。
円形コイルにおいて、導体の微小部分\(dl\)から点\(P\)に対して直線を引きます。ここで、
- 円形コイルの微小部分\(dl\)と点\(P\)との距離を\(R{\mathrm{[m]}}\)
- 円形コイルの中心\(O\)と点\(P\)との距離を\(y{\mathrm{[m]}}\)
- 円形コイルの中心\(O\)と導体の微小部分\(dl\)との距離を\(r{\mathrm{[m]}}\)
- 円形コイルの微小部分\(dl\)と点\(P\)との角度を\({\phi}\)
とします。この時、導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH\)はビオ・サバールの公式より次式となります。
\begin{eqnarray}
dH=\frac{1}{4{\pi}}{\cdot}\frac{I_1dl{\sin}{\theta}}{R^2}{\mathrm{[A/m]}}\tag{4-1}
\end{eqnarray}
ここで、円形コイルの微小部分\(dl\)の接線\(Q\)は点\(P\)に対して常に垂直(\({\theta}=90°=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\))となるため、『(\({\sin}{\theta}=1\))』となります。したがって、(4-1)式は次式となります。
\begin{eqnarray}
dH&=&\frac{1}{4{\pi}}{\cdot}\frac{I_1dl{\sin}{\theta}}{R^2}\\
&=&\frac{1}{4{\pi}}{\cdot}\frac{I_1dl×1}{R^2}\\
&=&\frac{I_1dl}{4{\pi}R^2}\tag{4-2}
\end{eqnarray}
ここで、上図より\(dH\)のx成分\(dH_{x}\)は微小部分\(dl\)が一周すると全て打ち消し合って『0』となるため、y成分\(dH_{y}\)のみを考えます。\(dH_{y}\)は次式で表されます。
\begin{eqnarray}
dH_{y}&=&dH{\sin}{\phi}\\
&=&\frac{I_1dl}{4{\pi}R^2}{\sin}{\phi}\tag{4-3}
\end{eqnarray}
導体の微小部分\(dl\)が作る磁界の強さ\(dH_{y}\)を積分することで、導体全体が作る磁界の強さ\(H_y\)を求めます。今回、円形コイルの導体全体を考えます。半径\(r\)の円形コイルの円周は\(2{\pi}r\)より、積分範囲は\(0~2{\pi}r\)となるため、(4-3)式を積分すると次式となります。
\begin{eqnarray}
H_y={\displaystyle\int}_{0}^{2{\pi}r}dH_{y}={\displaystyle\int}_{0}^{2{\pi}r}\frac{I_1}{4{\pi}R^2}{\sin}{\phi}dl{\mathrm{[A/m]}}\tag{4-4}
\end{eqnarray}
また、上図より以下の(4-5)式と(4-6)式を得ることができます。
\begin{eqnarray}
R=\sqrt{r^2+y^2}\tag{4-5}
\end{eqnarray}
\begin{eqnarray}
{\sin}{\phi}=\frac{r}{R}=\frac{r}{\sqrt{r^2+y^2}}\tag{4-6}
\end{eqnarray}
したがって、(4-5)式と(4-6)式を(4-4)式に代入すると、次式となります。
\begin{eqnarray}
H_y&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{I_1}{4{\pi}R^2}{\sin}{\phi}dl\\
&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{I_1}{4{\pi}\left(\sqrt{r^2+y^2}\right)^2}\frac{r}{\sqrt{r^2+y^2}}dl\\
&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{rI_1}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}dl\\
&=&\frac{rI_1}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}{\displaystyle\int}_{0}^{2{\pi}r}dl\\
&=&\frac{rI_1}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}\left[l\right]_{0}^{2{\pi}r}\\
&=&\frac{rI_1}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}×2{\pi}r\\
&=&\frac{r^2I_1}{2\left(r^2+y^2\right)^\frac{3}{2}}\tag{4-7}
\end{eqnarray}
そのため、磁束密度\(B_y{\mathrm{[T]}}\)は真空の透磁率\({\mu}_0=4{\pi}×10^{-7}\)を用いると、次式となります。
\begin{eqnarray}
B_y={\mu}_0H_y=\frac{{\mu}_0r^2I_1}{2\left(r^2+y^2\right)^\frac{3}{2}}\tag{4-8}
\end{eqnarray}
したがって、『円筒ソレノイドコイル』と交わる磁束\(d{\phi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
d{\phi}_2=B_yS=\frac{{\mu}_0r^2I_1S}{2\left(r^2+y^2\right)^\frac{3}{2}}\tag{4-9}
\end{eqnarray}
『円筒ソレノイドコイル』の微小部分\(dy\)の巻数は\(Ndy\)なので、『円筒ソレノイドコイル』の微小部分\(dy\)の磁束鎖交数\(d{\psi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
d{\psi}_2=Ndy×d{\phi}_2=\frac{{\mu}_0r^2I_1NS}{2\left(r^2+y^2\right)^\frac{3}{2}}dy\tag{4-10}
\end{eqnarray}
『円筒ソレノイドコイル』の長さは\(2r{\mathrm{[m]}}\)であり、その中心に『円形コイル』があるため、『円筒ソレノイドコイル』の全体の磁束鎖交数\({\psi}_2{\mathrm{[wb]}}\)は次式となります。
\begin{eqnarray}
{\psi}_2&=&{\displaystyle\int}_{-r}^{r}d{\psi}_2\\
&=&\frac{{\mu}_0r^2INS}{2}{\displaystyle\int}_{-r}^{r}\frac{1}{\left(r^2+y^2\right)^\frac{3}{2}}dy\\
&=&\frac{{\mu}_0NSI_1}{\sqrt{2}}\tag{4-11}
\end{eqnarray}
『円形コイル』に流れている電流\(I_1\)、『円筒ソレノイドコイル』の磁束鎖交数\({\psi}_2\)、相互インダクタンス\(M\)の関係は『\({\psi}_2=MI_1\)』なので、『円形コイル』と『円筒ソレノイドコイル』との間の相互インダクタンス\(M\)は次式となります。
\begin{eqnarray}
M=\frac{{\psi}_2}{I_1}=\frac{\displaystyle\frac{{\mu}_0NSI_1}{\sqrt{2}}}{I_1}=\frac{{\mu}_0NS}{\sqrt{2}}{\mathrm{[H]}}\tag{4-12}
\end{eqnarray}
まとめ
この記事では相互インダクタンスに関する様々な例題について説明しました。
相互インダクタンス\(M\)は、1つのコイルに電流\(I_1\)を流した時において、他方のコイルと鎖交する磁束数\({\psi}_2\)を求めて、『\({\psi}_2=MI_1\)』の式に代入することで、求めることができます。
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。