【ガウスの発散定理とは？】『公式』や『意味』などを解説！

この記事では『ガウスの発散定理』について

『ガウスの発散定理』の公式と意味

などを図を用いて分かりやすく説明しています。

ガウスの発散定理とは

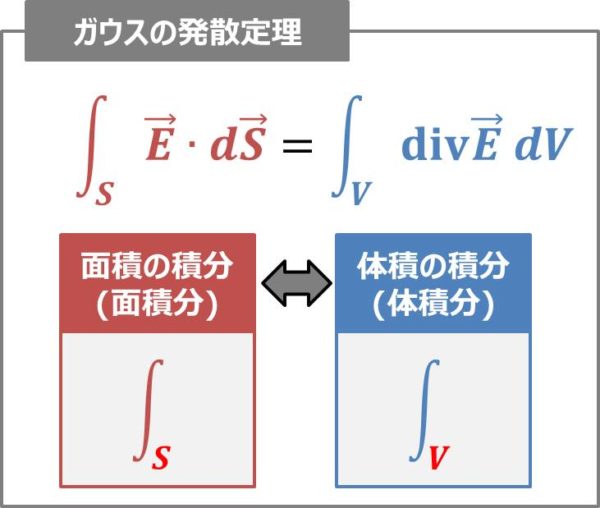
ガウスの発散定理とは、面積の積分(面積分)と体積の積分(体積分)の関係を表す公式であり、次式となります。

ガウスの発散定理の公式

面積ベクトル\(d{\vec{S}}\)を用いる場合

\begin{eqnarray}
\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

法線ベクトル\({\vec{n}}\)を用いる場合

\begin{eqnarray}
\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}{\vec{n}}{\;}dS=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

上式の左辺は面積分、右辺は体積分を表しています。このガウスの発散定理は、式から分かるように『面積分⇔体積分』の変換に用います。

上式だけだとイメージが湧かないと思いますので、次にガウスの発散定理の意味について説明します。

補足

ガウスの発散定理は英語では「Gauss's divergence theorem」と書きます。

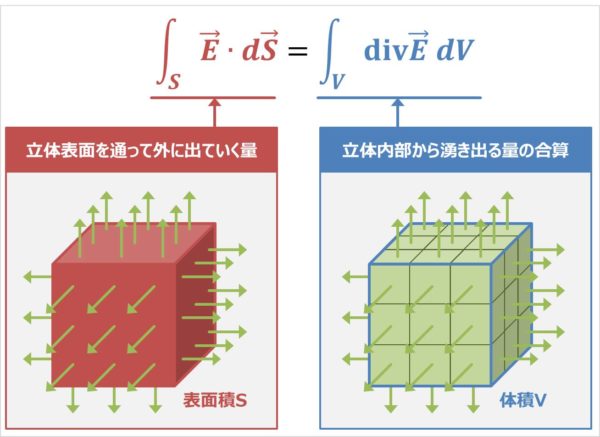
ガウスの発散定理の意味

ガウスの発散定理の意味ですが、分かりやすく解釈すると、

ガウスの発散定理の意味

ある立体があって、立体内部から何らかの量(例えば、水や電気力線など)が湧き出ているとします。その時、立体内部から湧き出る量の合算\(\left(\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV\right)\)は、立体表面を通って外に出ていく量\(\left(\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\right)\)と同じになる。というのがガウスの発散定理の意味となっています。

湧きだしたものが外に出ていく・・・当たり前といえば当たり前ですね。

では次に、立体内部から湧き出る量の合算\(\left(\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV\right)\)と立体表面を通って外に出ていく量\(\left(\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\right)\)について少し詳しく説明します。

立体内部から湧き出る量の合算

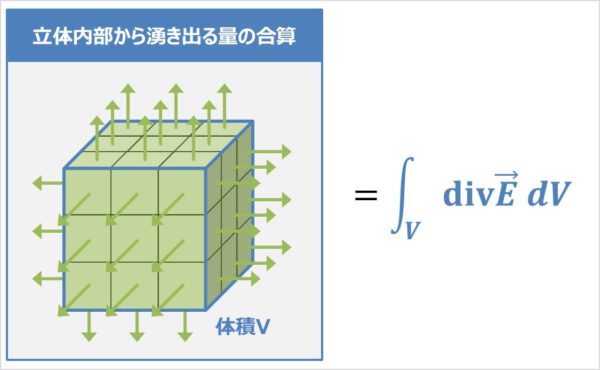
体積\(V\)の立体内部から湧き出る\({\vec{E}}\)の量の合算は次式で表されます。

\begin{eqnarray}
体積Vの立体内部から湧き出る{\vec{E}}の量の合算=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

上式の意味

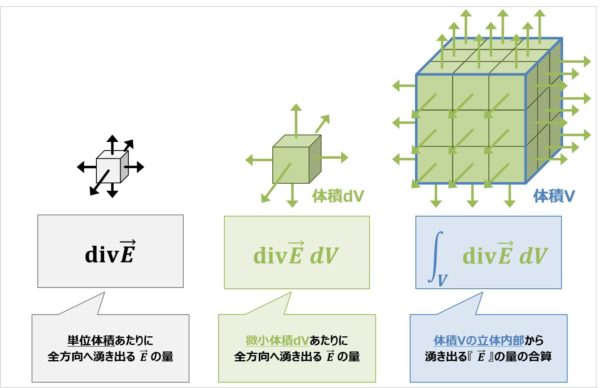
まず『\({\mathrm{div}}{\vec{E}}\)』について説明します。

『\({\mathrm{div}}{\vec{E}}\)』とは、単位体積あたりに全方向へ湧き出る\({\vec{E}}\)の量のことを意味しています。

そのため、微小体積\(dV\)の立体から全方向へ湧き出る\({\vec{E}}\)の量は『\({\mathrm{div}}{\vec{E}}\)』に微小体積の『\(dV\)』を掛ければよいので、

\begin{eqnarray}
微小体積dVの立体から全方向へ湧き出る{\vec{E}}の量={\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

となります。

したがって、体積\(V\)の立体内部から湧き出る\({\vec{E}}\)の量の合算は、微小体積\(dV\)の立体から湧き出る\({\vec{E}}\)の量(\({\mathrm{div}}{\vec{E}}{\;}dV\))を足し合わせる(=体積分する)と求めることができ、

\begin{eqnarray}
体積Vの立体内部から湧き出る{\vec{E}}の量の合算=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

となります。

ここで、上式について、少し詳細に説明します。

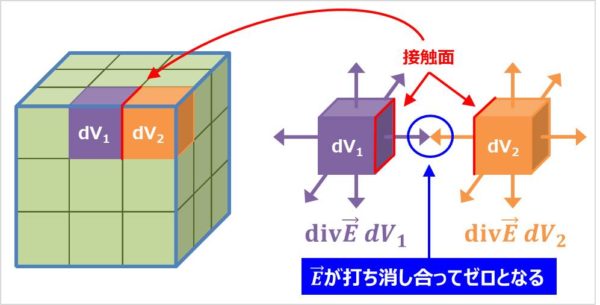
体積\(V\)は、微小体積\(dV\)の足し合わせでできています。

ここで、微小体積\(dV_{1}\)から湧き出る\({\vec{E}}\)の量(\({\mathrm{div}}{\vec{E}}{\;}dV_{1}\))と隣り合っている微小体積\(dV_{2}\)から湧き出る\({\vec{E}}\)の量(\({\mathrm{div}}{\vec{E}}{\;}dV_{2}\))を考えてみます。

微小体積\(dV_{1}\)の『\({\mathrm{div}}{\vec{E}}{\;}dV_{1}\)』と微小体積\(dV_{2}\)の『\({\mathrm{div}}{\vec{E}}{\;}dV_{2}\)』の接触面においては\({\vec{E}}\)の向きが反対となっています。そのため、隣り合っている箇所においては、湧き出ている\({\vec{E}}\)が打ち消し合ってゼロとなるのです。

つまり、何がいいたいのかというと・・・

体積\(V\)の立体内部から湧き出る\({\vec{E}}\)の量の合算は、微小体積\(dV\)から湧き出る\({\vec{E}}\)の量(\({\mathrm{div}}{\vec{E}}{\;}dV\))を足し合わせる(=積分する)ことで求めることができますが、隣り合っている箇所においては湧き出ている\({\vec{E}}\)が互いに打ち消し合うため、結局のところ、立体の表面からのみ\({\vec{E}}\)が湧き出ているということになる。

ということです。では、次に立体の表面から湧き出ている\({\vec{E}}\)の量(立体表面を通って外に出ていく\({\vec{E}}\)の量)を式で表してみましょう。

立体表面を通って外に出ていく量

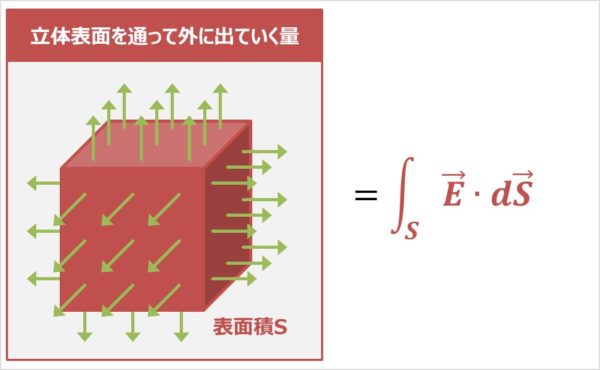
表面積\(S\)の立体表面から湧き出ている\({\vec{E}}\)の量(立体表面を通って外に出ていく\({\vec{E}}\)の量)は次式で表されます。

\begin{eqnarray}
表面積Sの立体表面を通って外に出ていく{\vec{E}}の量=\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}
\end{eqnarray}

上式の意味

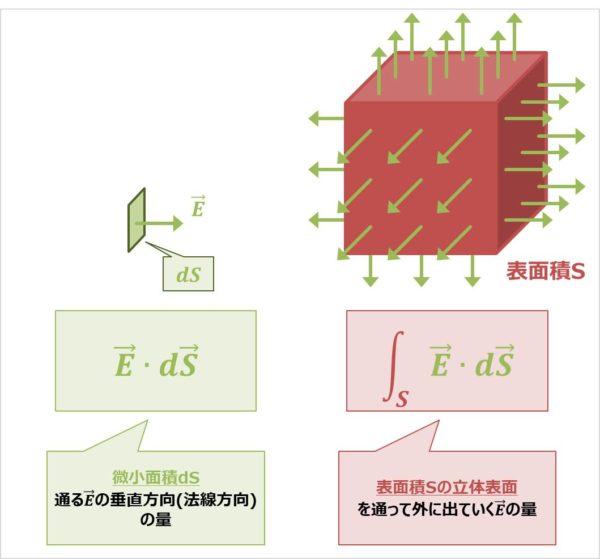
まず、『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』について説明します。

『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』とは、微小面積\(dS\)を通る\({\vec{E}}\)の垂直方向(法線方向)の量のことを意味しています。

したがって、表面積\(S\)の立体表面を通って外に出ていく\({\vec{E}}\)の量は、微小面積\(dS\)を通る\({\vec{E}}\)の垂直方向(法線方向)の量(\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\))を足し合わせる(=面積分する)と求めることができ、

\begin{eqnarray}
表面積Sの立体表面を通って外に出ていく{\vec{E}}の量=\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}
\end{eqnarray}

となります。

したがって、今までのことをまとめると、

体積\(V\)の立体内部から湧き出る\({\vec{E}}\)の量の合算\(\left(\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV\right)\)は、微小体積\(dV\)から湧き出る\({\vec{E}}\)の量(\({\mathrm{div}}{\vec{E}}{\;}dV\))を足し合わせる(=積分する)ことで求めることができますが、隣り合っている箇所においては湧き出ている\({\vec{E}}\)が互いに打ち消し合うため、結局のところ、表面積\(S\)の立体表面から湧き出ている\({\vec{E}}\)の量(立体表面を通って外に出ていく\({\vec{E}}\)の量)\(\left(\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\right)\)になる。

となります。これを式で表したのがガウスの発散定理の公式であり、

ガウスの発散定理の公式

\begin{eqnarray}
\displaystyle\int_{S}{\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}=\displaystyle\int_{V}{\mathrm{div}}{\vec{E}}{\;}dV
\end{eqnarray}

となるのです。

【補足】E・dSって何？

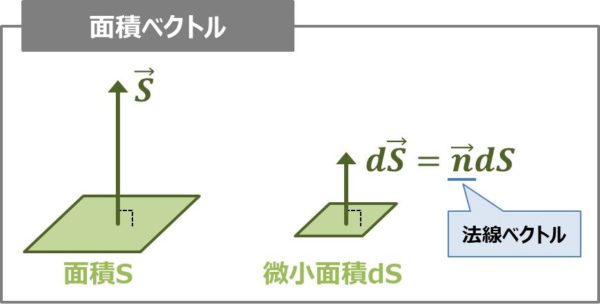
ここでは、『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』について説明します。

まず、面積である\(S\)にベクトルが付いた\({\vec{S}}\)について説明します。

これは、面積ベクトルと呼ばれるものであり、向きが面に垂直な方向(法線方向)で、大きさが\(S\)に等しいベクトルのことを指します。すなわち、\(d{\vec{S}}\)とは、向きが微小体積\(dS\)に垂直な方向(法線方向)で、大きさが\(dS\)に等しいベクトルのことを指します。法線ベクトル\({\vec{n}}\)を用いると次式で表されます。

\begin{eqnarray}
d{\vec{S}}={\vec{n}}dS
\end{eqnarray}

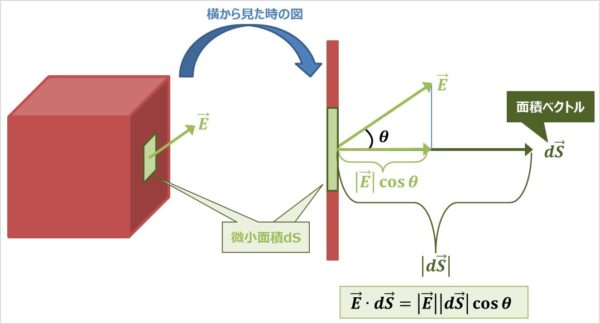
また、立体表面から湧き出ている\({\vec{E}}\)は立体表面から必ずしも垂直に出ているとは限りません。そのため、\({\vec{E}}\)の垂直成分の大きさを求める必要があります。例えば、上図の場合では、\({\vec{E}}\)の垂直成分の大きさは

\begin{eqnarray}
{\vec{E}}の垂直成分の大きさ=|{\vec{E}}|{\;}{\cos{\theta}}
\end{eqnarray}

となります。また、面積ベクトル\(d{\vec{S}}\)の大きさは

\begin{eqnarray}
d{\vec{S}}の大きさ=|d{\vec{S}}|
\end{eqnarray}

となります。これを掛け算すると、微小面積\(dS\)を通る\({\vec{E}}\)の垂直方向(法線方向)の量を求めることができます。

\begin{eqnarray}
微小面積dSを通る{\vec{E}}の垂直方向(法線方向)の量=|{\vec{E}}||d{\vec{S}}|{\;}{\cos{\theta}}
\end{eqnarray}

上式は内積の公式によって、
\begin{eqnarray}
微小面積dSを通る{\vec{E}}の垂直方向(法線方向)の量=|{\vec{E}}||d{\vec{S}}|{\;}{\cos{\theta}}={\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}
\end{eqnarray}
に変形できます。

これより、『\({\vec{E}}{\;}{\cdot}{\;}d{\vec{S}}\)』は、微小面積\(dS\)を通る\({\vec{E}}\)の垂直方向(法線方向)の量のことを意味しているということになります。