フィルタ回路(ローパスフィルタやハイパスフィルタなど)において、カットオフ周波数(遮断周波数)でゲインが-3dBになる理由と、ゲインが-3dBとなる時の電力と電圧について説明します。
カットオフ周波数における電力利得(ゲイン)について
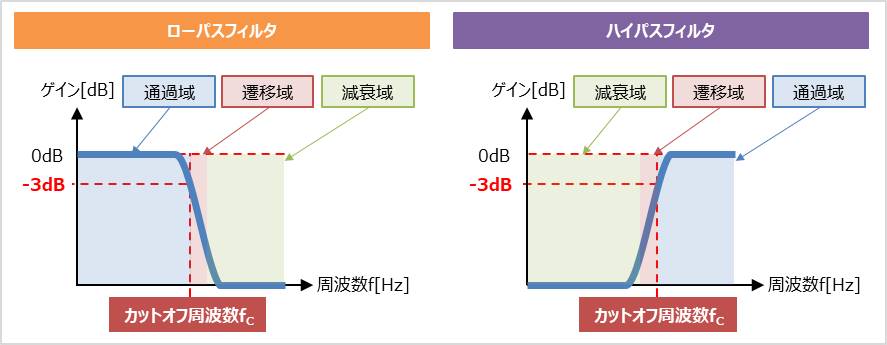
カットオフ周波数(遮断周波数、コーナー周波数、3dBポイント)とは、フィルタ回路において、通過域と遷移域の境界となる周波数です。なお、参考書によっては、遷移域の箇所も減衰域と定義している場合があります。この場合、通過域と減衰域の境界となる周波数がカットオフ周波数となります。
ローパスフィルタに入力する電圧の周波数を上げると、出力電圧はやがて減少し始めます(つまり減衰します)。一方、ハイパスフィルタでは、入力する電圧の周波数を上げると、出力電圧はやがて増加し始めます(つまり増幅します)。カットオフ周波数\(f_{C}\)では、出力電圧の振幅が通過域平坦部の0.707倍、電力で考えると出力電力が通過域平坦部の半分になり、この時、ゲインが-3dBとなります。
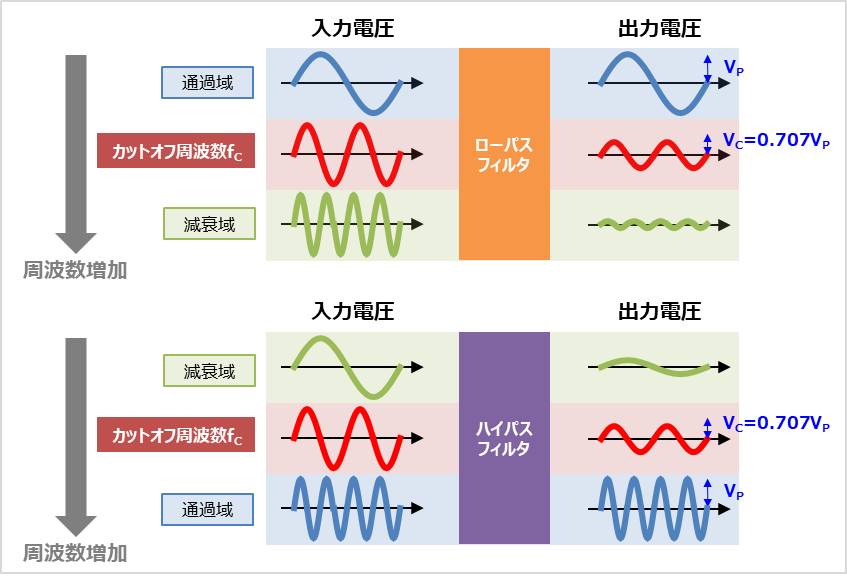
これから、ゲインが-3dBになる理由を式を用いて説明します。
ある基準となる電力\(P_{1}\)に対して、比較対象となる電力\(P_{2}\)が何倍になったかを表す電力比(電力利得、ゲイン)\(G_{V}\)をデシベル(dB)で表現すると以下の式となります。
G_{P}=10{\log_{10}}\left(\frac{P_{2}}{P_{1}}\right)
\end{eqnarray}
今回、ある基準となる電力を通過域(Pass Band)での電力\(P_{P}\)、比較対象となる電力をカットオフ周波数\(f_{C}\)での電力\(P_{C}\)とすると、ゲインは以下の式となります。
\begin{eqnarray}
G_{P}=10{\log_{10}}\left(\frac{P_{C}}{P_{P}}\right) \tag{1}
\end{eqnarray}
ここで、カットオフ周波数\(f_{C}\)での電力\(P_{C}\)は通過域(Pass Band)での電力\(P_{P}\)の半分なので、(1)式は以下の式となります。
\begin{eqnarray}
G_{P}&=&10{\log_{10}}\left(\frac{P_{C}}{P_{P}}\right)\\
&=&10{\log_{10}}\left(\frac{1}{2}\right)\\
&=&-3[dB] \tag{2}
\end{eqnarray}
ゲインが-3dBとなりました。このように、カットオフ周波数\(f_{C}\)は電力で考えると、フィルタ回路に入力する電力の半分がフィルタ回路を通過し、半分が遮断される時の周波数となります。つまり、電力の半分がフィルタ回路を通過できなくなるポイントを表します。
カットオフ周波数における電圧利得(ゲイン)について
ある基準となる電圧\(V_{1}\)に対して、比較対象となる電圧\(V_{2}\)が何倍になったかを表す電圧比(電圧利得、ゲイン)\(G_{V}\)をデシベル(dB)で表現すると以下の式となります。
G_{V}=20{\log_{10}}\left(\frac{V_{2}}{V_{1}}\right)
\end{eqnarray}
今回、ある基準となる電圧を通過域(Pass Band)での電圧振幅\(V_{P}\)、比較対象となる電圧をカットオフ周波数\(f_{C}\)での電圧振幅\(V_{C}\)とすると、ゲインは以下の式となります。
\begin{eqnarray}
G_{V}=20{\log_{10}}\left(\frac{V_{C}}{V_{P}}\right) \tag{3}
\end{eqnarray}
また、カットオフ周波数\(f_{C}\)では、ゲイン\(G_{V}\)は-3dBとなるので、(3)式は以下の式となります。
\begin{eqnarray}
-3dB&=&20{\log_{10}}\left(\frac{V_{C}}{V_{P}}\right)\\
{\Leftrightarrow}V_{C}&=&\frac{1}{\sqrt{2}}V_{P}=0.707V_{P}
\end{eqnarray}
このように、カットオフ周波数\(f_{C}\)は電圧で考えると、フィルタ回路に入力する電圧の振幅(通過域での電圧振幅\(V_{P}\))が0.707倍になるとき時の周波数となります。






