この記事ではカレントミラー(Current Mirror)について基本的な内容から等価回路や原理まで詳しく説明します。
カレントミラーとは?
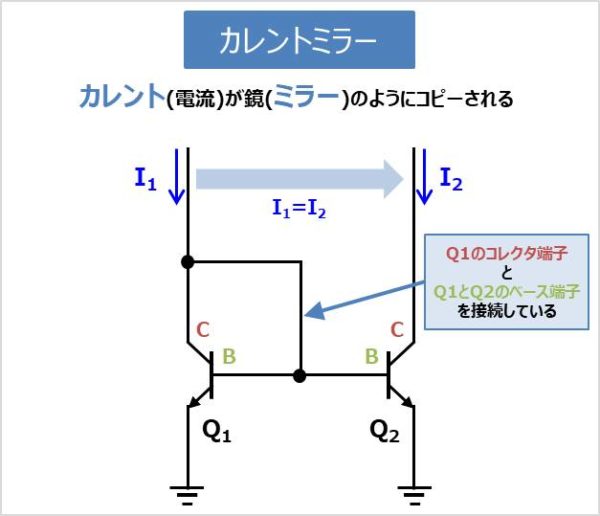
カレントミラー(Current Mirror)とは、名前の通り、カレント(電流)をミラー(鏡)のようにコピーする回路となります。カレントミラー回路で一番有名で基本的な回路を上図に説明します。バイポーラトランジスタ\(Q_{1}\)のコレクタ端子とバイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のベース端子を接続している構成となっています。
カレントミラー回路の原理は後ほど説明しますが、カレントミラー回路に対して、電流\(I_{1}\)を流すと、バイポーラトランジスタ\(Q_{2}\)のコレクタにも電流\(I_{2}\)が流れます。電流\(I_{1}\)がミラー(鏡)のように電流\(I_{2}\)にコピーされるので、カレントミラー回路と呼ばれています。
カレントミラーの等価回路
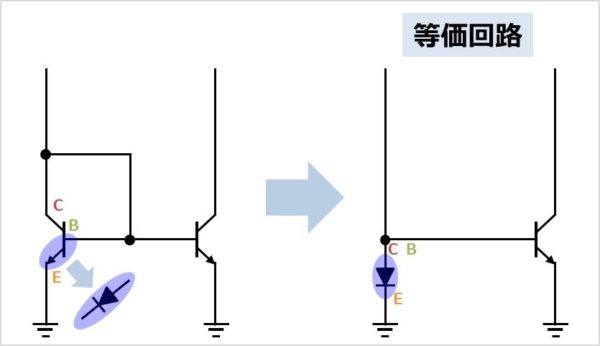
バイポーラトランジスタ\(Q_{1}\)のベース(B)とエミッタ(E)はPN接合なので、ダイオードのように表されます。そして、コレクタ(C)とベース(B)を接続してるので等価回路は上図のようになります。このように、バイポーラトランジスタのコレクタ(C)とベース(B)を結合している場合、コレクタ(C)とベース(B)がダイオードのアノードとなり、エミッタがカソードとなります。
カレントミラーの原理と計算方法
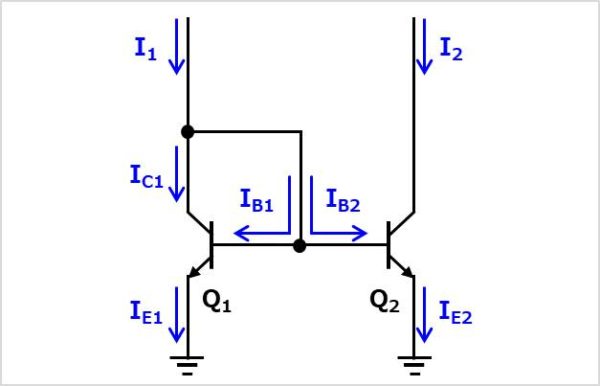
少し計算が複雑ですが、電流\(I_{1}\)と電流\(I_{2}\)が等しくなる原理を計算式を用いて説明します。
電流\(I_{1}\)の値の導出
バイポーラトランジスタ\(Q_{1}\)のエミッタ電流\(I_{E1}\)はバイポーラトランジスタ\(Q_{1}\)のコレクタ電流\(I_{C1}\)とベース電流\(I_{B1}\)の合計値となりますので、以下の式が成り立ちます。
\begin{eqnarray}
I_{E1}= I_{C1}+ I_{B1} \tag{1}
\end{eqnarray}
電流\(I_{1}\)はバイポーラトランジスタ\(Q_{1}\)のコレクタ電流\(I_{C1}\)とベース電流\(I_{B1}\)、バイポーラトランジスタ\(Q_{2}\)のベース電流\(I_{B2}\)の合計値となりますので、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}= I_{C1}+ I_{B1}+ I_{B2}= I_{E1}+ I_{B2}\tag{2}
\end{eqnarray}
電流\(I_{2}\)の値の導出
バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のベース電圧は等しいため、バイポーラトランジスタ\(Q_{1}\)とバイポーラトランジスタ\(Q_{2}\)の特性が等しい場合、バイポーラトランジスタ\(Q_{1}\)のエミッタ電流\(I_{E1}\)とバイポーラトランジスタ\(Q_{2}\)のエミッタ電流\(I_{E2}\)が等しくなりますので、以下の式が成り立ちます。
\begin{eqnarray}
I_{E1}= I_{E2} \tag{3}
\end{eqnarray}
電流\(I_{2}\)とバイポーラトランジスタ\(Q_{2}\)のベース電流\(I_{B2}\)の合計がコレクタ電流\(I_{E2}\)の合計値となりますので、以下の式が成り立ちます。
\begin{eqnarray}
I_{E2}&=&I_{2}+ I_{B2}\\
{\Leftrightarrow}I_{2}&= &I_{E2}- I_{B2}= I_{E1}- I_{B2} \tag{4}
\end{eqnarray}
電流\(I_{1}\)と電流\(I_{2}\)の関係
(2)式と(4)式を用いると、電流\(I_{1}\)と電流\(I_{2}\)の関係式は以下のようになります。
\begin{eqnarray}
I_{1}- I_{2}=2I_{B2}\tag{5}
\end{eqnarray}
ここで、バイポーラトランジスタ\(Q_{2}\)の直流電流増幅率hFEが大きく、ベース電流\(I_{B2}\)を無視すると、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}=I_{2} \tag{6}
\end{eqnarray}
これよりカレントミラーにおいて電流\(I_{1}\)と電流\(I_{2}\)が等しくなりました。
補足
- 式の導出では、バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)の直流電流増幅率hFEが大きいと仮定し、ベース電流\(I_{B2}\)を無視しましたが、厳密には、(5)式より電流\(I_{1}\)は電流\(I_{2}\)よりも\(2I_{B2}\)だけ大きくなります。電流\(I_{1}\)に電流\(I_{2}\)を近づけるには、バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)に高い直流増幅率hFEを持つものを使用する必要があります。
- バイポーラトランジスタ\(Q_{1}\)のエミッタ電流\(I_{E1}\)とバイポーラトランジスタ\(Q_{2}\)のエミッタ電流\(I_{E2}\)を等しくするためには、バイポーラトランジスタ\(Q_{1}\)とバイポーラトランジスタ\(Q_{2}\)の特性を等しくすることが、重要となります。バイポーラトランジスタは温度特性を持っており、温度によって、エミッタ電流が変化してしまうため、バイポーラトランジスタ\(Q_{1}\)とバイポーラトランジスタ\(Q_{2}\)を熱結合して、温度条件を同一にそろえる必要があります。そのため、2素子を1つのシリコン基板上に実装してあるモノリシック・デュアルタイプのトランジスタを利用することをオススメします。
- バイポーラトランジスタ\(Q_{1}\)のコレクタ電圧とバイポーラトランジスタ\(Q_{2}\)のベース電圧が同電位です。そのため、バイポーラトランジスタ\(Q_{2}\)のコレクターエミッタ間電圧はバイポーラトランジスタ\(Q_{1}\)のコレクターエミッタ間電圧より大きくなります。また、バイポーラトランジスタ\(Q_{2}\)にかかる電圧が変化すると、電流\(I_{2}\)はアーリー効果の影響を受けて変化します。
PNP型のカレントミラー
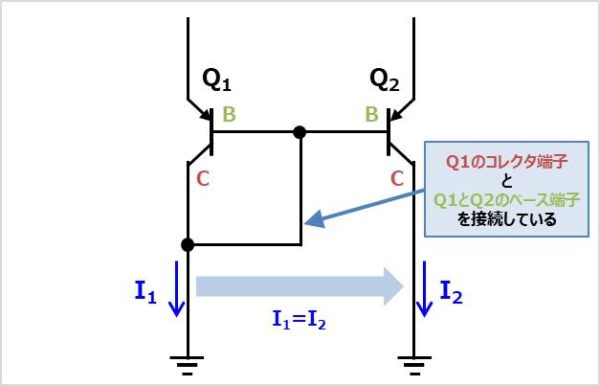
PNP型のカレントミラーを上図に示します。NPN型と同じく、バイポーラトランジスタ\(Q_{1}\)のコレクタ端子とバイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のベース端子を接続している構成となっています。






