カレントミラーには様々な種類があります。この記事では8種のカレントミラーについて特徴を説明します。
カレントミラー
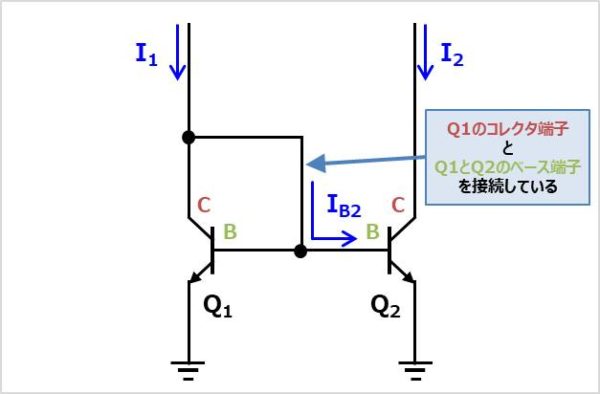
カレントミラー(current mirror)とは、名前の通り、カレント(電流)をミラー(鏡)のように映しコピーする回路となります。カレントミラーで一番有名で基本的な回路を上図に説明します。バイポーラトランジスタ\(Q_{1}\)のコレクタ端子とバイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のベース端子を接続している構成となっており、電流\(I_{1}\)と電流\(I_{2}\)が等しくなるのが特徴です。
このタイプのカレントミラーについては、以下の記事で詳しく説明しています。 続きを見る

『カレントミラー』とは?等価回路や原理について詳しく説明します!
このカレントミラー回路は厳密には電流\(I_{1}\)と電流\(I_{2}\)が等しくならず、電流\(I_{1}\)は電流\(I_{2}\)によりも\(2I_{B2}\)だけ大きくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}= I_{2}+2I_{B2}
\end{eqnarray}
また、バイポーラトランジスタ\(Q_{2}\)にかかる電圧が変化すると、電流\(I_{2}\)はアーリー効果の影響を受けて変化するという欠点があります。
エミッタ抵抗接続型カレントミラー
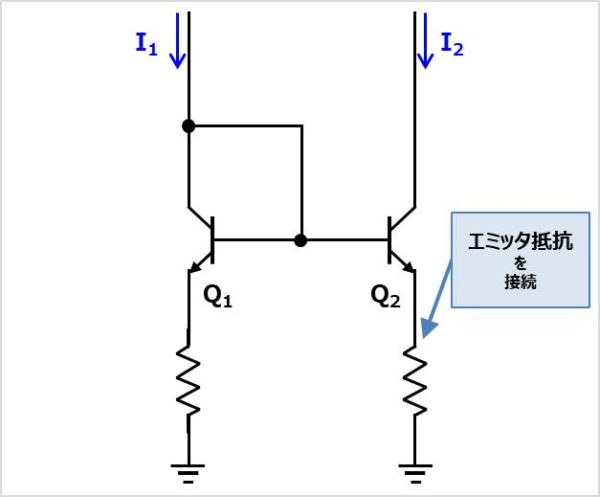

2つのバイポーラトランジスタにおいて、特性や温度のズレがあると、電流\(I_{1}\)と電流\(I_{2}\)の値が大きく異なってしまいます。そこでエミッタに抵抗を接続することで精度と安定性を高めた回路となっています。
ベース電流補償型カレントミラー
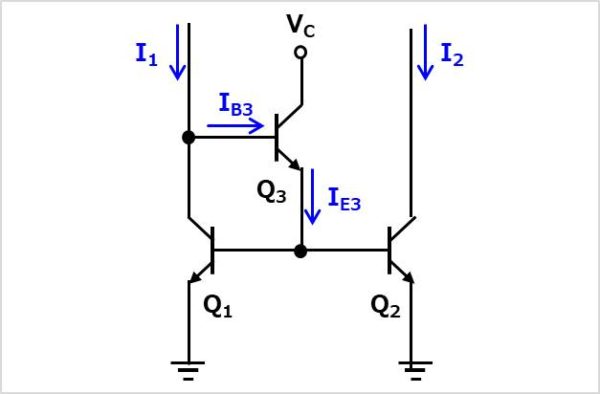

ベース電流供給用のバイポーラトランジスタ\(Q_{3}\)を追加した回路です。ベース電流\(I_{B3}\)よりもエミッタ電流\(I_{E3}\)の方が大きいため、電流\(I_{1}\)の分流量が小さくなり、誤差が小さくなります。
MOSFETを使用したカレントミラー
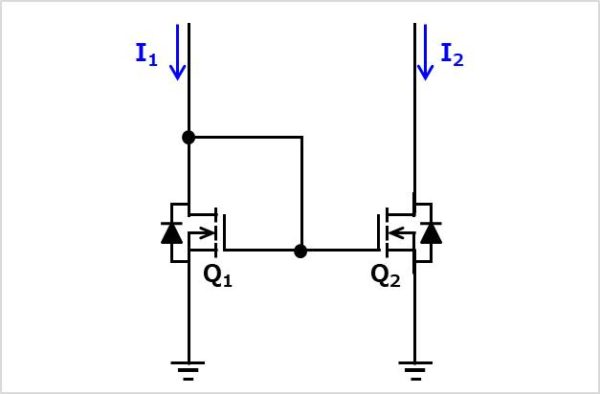

バイポーラトランジスタを使用したカレントミラー回路では、ベース電流による誤差があります。このベース電流の誤差を無くすためにバイポーラトランジスタをMOSFETに変更した回路です。しかし、MOSFETはバイポーラトランジスタよりもバラツキが大きいという欠点があります。
ウィルソンカレントミラー
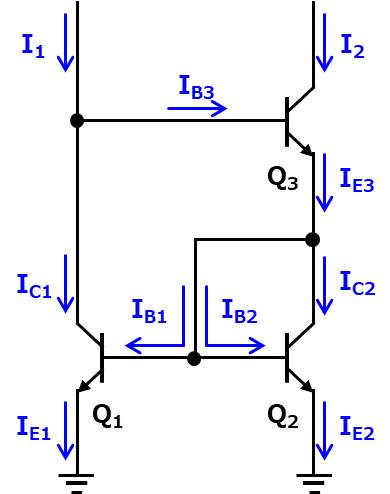

一般的なカレントミラーで問題となるアーリー効果やベース電流の影響を低減した回路です。バイポーラトランジスタ\(Q_{3}\)によって、バイポーラトランジスタ\(Q_{2}\)のコレクタ電圧をほとんど一定にすることで、アーリー効果を対策しています。
ウィルソンカレントミラーでは、ベース電流\(I_{B3}\)とベース電流\(I_{B1}\)が等しい場合に、電流\(I_{1}\)と電流\(I_{2}\)が等しくなります。
電流\(I_{1}\)と電流\(I_{2}\)が等しくなる原理を説明します。
バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のベース電圧は等しいため、バイポーラトランジスタ\(Q_{1}\)とバイポーラトランジスタ\(Q_{2}\)の特性が等しい場合、バイポーラトランジスタ\(Q_{1}\)のエミッタ電流\(I_{E1}\)とバイポーラトランジスタ\(Q_{2}\)のエミッタ電流\(I_{E2}\)が等しくなりますので、以下の式が成り立ちます。
\begin{eqnarray}
I_{E1}= I_{E2} \tag{1}
\end{eqnarray}
また、電流\(I_{1}\)はバイポーラトランジスタ\(Q_{1}\)のコレクタ電流\(I_{C1}\)とバイポーラトランジスタ\(Q_{3}\)のベース電流\(I_{B3}\)に分流します。そのため、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}= I_{C1}+ I_{B3}\tag{2}
\end{eqnarray}
バイポーラトランジスタ\(Q_{1}\)のエミッタ電流\(I_{E1}\)はバイポーラトランジスタ\(Q_{1}\)のコレクタ電流IC1とバイポーラトランジスタ\(Q_{3}\)のベース電流\(I_{B1}\)の足し算なので以下の式が成り立ちます。
\begin{eqnarray}
I_{E1}= I_{C1}+ I_{B1} \tag{3}
\end{eqnarray}
ここで、ベース電流\(I_{B1}\)とベース電流\(I_{B1}\)が等しい場合、以下の式が成り立ちます。
\begin{eqnarray}
I_{E1}= I_{C1}+ I_{B1} = I_{C1}+ I_{B3}= I_{1}\tag{4}
\end{eqnarray}
また、ベース電流\(I_{B2}\)とベース電流\(I_{B1}\)が等しいため、キルヒホッフの電流則より、バイポーラトランジスタ\(Q_{2}\)のエミッタ電流\(I_{E2}\)と電流\(I_{2}\)が等しくなります。
\begin{eqnarray}
I_{E2}= I_{2} \tag{5}
\end{eqnarray}
しががって、(1)式、(4)式、(5)式より
\begin{eqnarray}
I_{1}= I_{2} \tag{6}
\end{eqnarray}
となります。
高精度ウィルソンカレントミラー
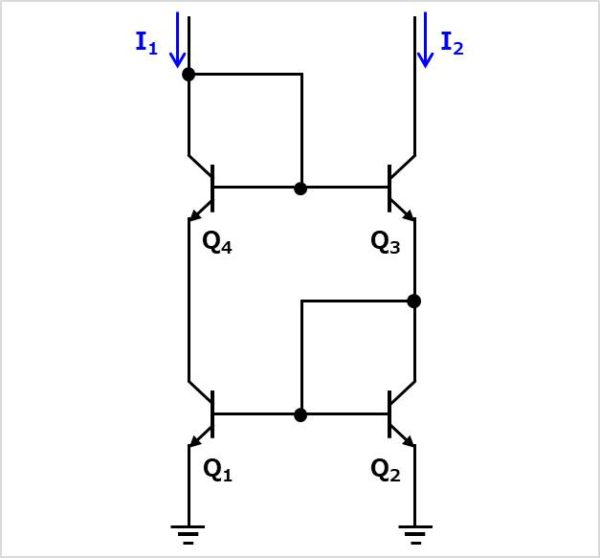

バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のコレクタ電圧を等しくするために、ウィルソンカレントミラーに対してバイポーラトランジスタ\(Q_{4}\)を追加した回路です。バイポーラトランジスタ\(Q_{1}\)と\(Q_{2}\)のコレクタ電圧が等しくなることで、温度ドリフトが減り、「\(I_{1}= I_{2}\)」が高精度で達成できるようになります。
多出力のカレントミラー
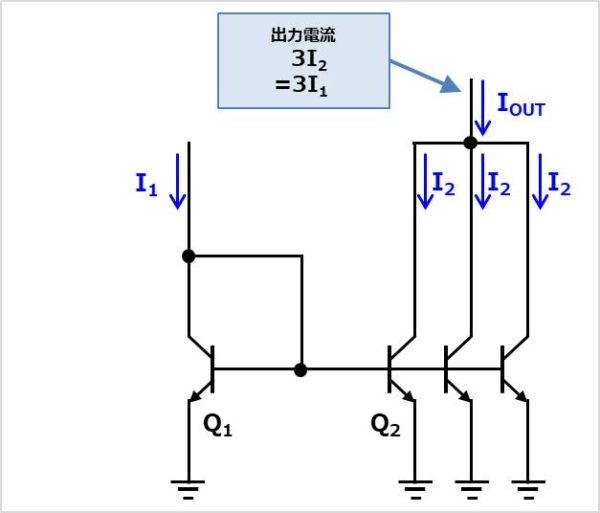

入力側のバイポーラトランジスタ、出力側のバイポーラトランジスタを並列接続した回路です。例えば、出力側のバイポーラトランジスタ\(Q_{2}\)を上図のように3個並列にすると、出力電流\(I_{OUT}\)は以下の式で表されます。
\begin{eqnarray}
I_{OUT}= 3I_{2}= 3I_{1}
\end{eqnarray}
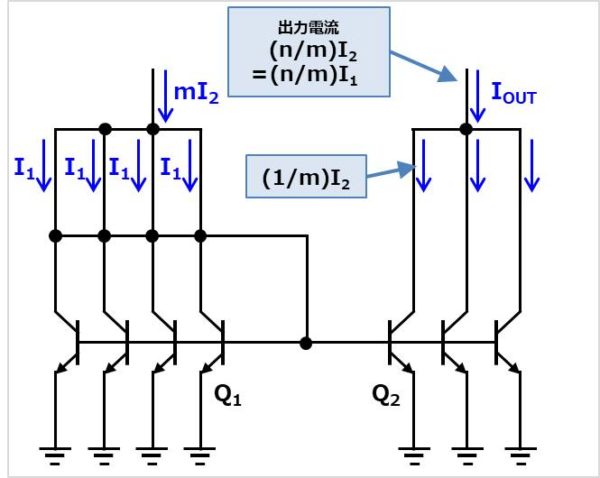

また、上図のように、入力側のバイポーラトランジスタ\(Q_{1}\)をm個、出力側のバイポーラトランジスタ\(Q_{2}\)をn個並列に接続すると、出力電流\(I_{OUT}\)は以下の式で表されます。
\begin{eqnarray}
I_{OUT}= \frac{n}{m} I_{2}=\frac{n}{m}I_{1}
\end{eqnarray}






