電流の有名な公式の1つに『I=envS』という式があります。
この『I=envS』とはどのような意味を持つか知っていますでしょうか?
この記事では、『I=envS』の導出や覚え方などを図を用いて分かりやすく説明しています。
『I=envS』については、式の導出過程が出題されることもあれば、『I=envS』の公式を用いた計算問題が出題されることもありますので、しっかり理解していきましょう!
『I=envS』の公式
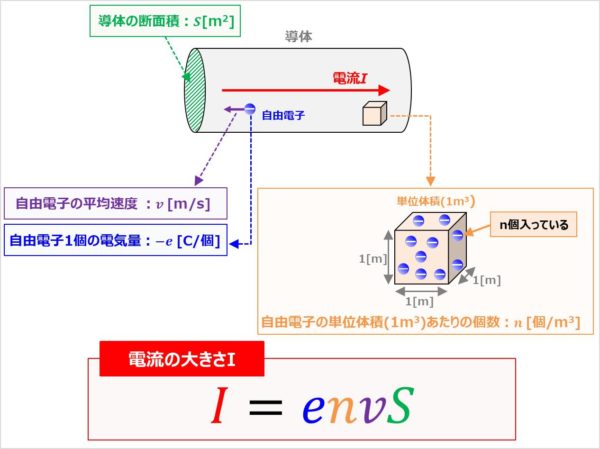
自由電子の単位体積(1m3)あたりの個数(数密度と呼ばれる)をn[個/m3]、自由電子の平均速度をv[m/s]、導体の断面積をS[m2]とすると、電流の大きさIは次式となります。
I=envS
なお、上式のeは『負電荷の自由電子1個の電気量の絶対値または正電荷の陽子1個の電気量』であり、電子素量と呼ばれるものです。
- 負電荷の自由電子1個が持つ電気量:-e=-1.6×10-19[C/個]
- 正電荷の陽子1個が持つ電気量:e=1.6×10-19[C/個]
となります。
では、次に、『I=envS』の導出について図を用いて分かりやすく説明します。
補足
- 電子素量の単位は[C]で表すのが一般的です。本記事では自由電子1個の電荷量を表すために、[C/個]で表しています。単位を[C/個]にすることで、この後に説明する『I=envS』の導出が分かりやすくなります。
- 電気素量は素電荷とも呼ばれています。
『I=envS』の導出
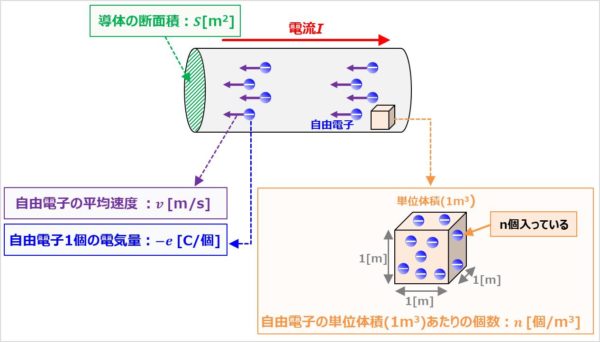
上図は断面が円の銅線に多くの自由電子が流れているイメージ図となっています。
『I=envS』の導出においては、自由電子の単位体積(1m3)あたりの個数(数密度)をn[個/m3]、自由電子の平均速度をv[m/s]、導体の断面積をS[m2]とします。
この『I=envS』の導出について以下の流れで説明していきます。
- 1秒間に自由電子が進む距離を求める
- 1秒間に導体の断面を通過する体積を求める
- 1秒間に導体の断面を通過する自由電子の数を求める
- 1秒間に導体の断面を通過する電気量を求める
- 電流の大きさの式『I=envS』が完成!
①1秒間に自由電子が進む距離を求める
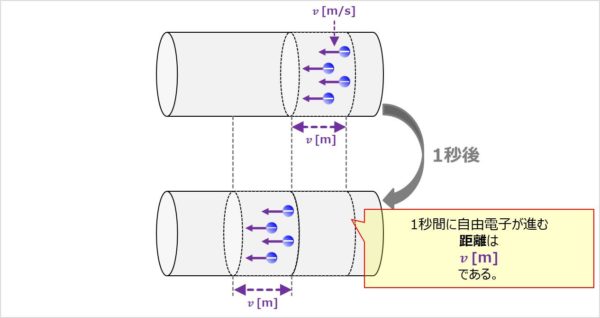
自由電子の平均速度はv[m/s]なので、1秒間(t=1[s])に自由電子が進む距離は
\begin{eqnarray}
v{\mathrm{[m/s]}}×1{\mathrm{[s]}}=v{\mathrm{[m]}}
\end{eqnarray}
となります。
①1秒間に導体の断面を通過する体積を求める
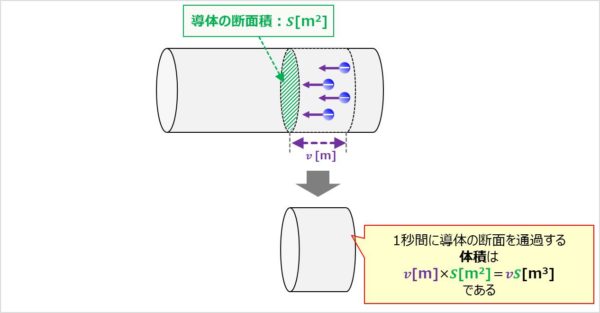
導体の断面積はS[m2]なので、1秒間に導体の断面を通過する体積は、
\begin{eqnarray}
v{\mathrm{[m]}}×S{\mathrm{[m^2]}}=vS{\mathrm{[m^3]}}
\end{eqnarray}
となります。
③1秒間に導体の断面を通過する自由電子の数を求める
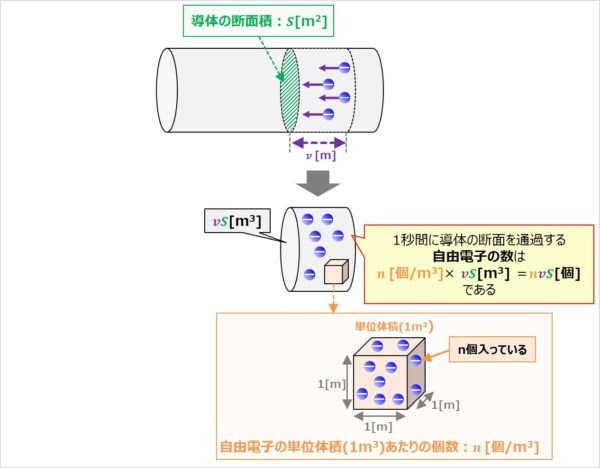
自由電子の単位体積(1m3)あたりの個数(数密度)はn[個/m3]なので、1秒間に導体の断面を通過する自由電子の数は、
\begin{eqnarray}
n{\mathrm{[個/m^3]}}×vS{\mathrm{[m^3]}}=nvS{\mathrm{[個]}}
\end{eqnarray}
となります。
④1秒間に導体の断面を通過する電気量を求める
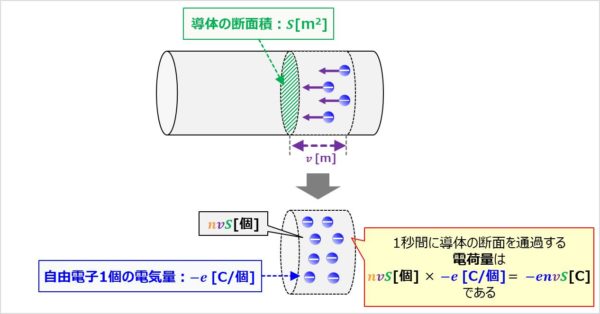
自由電子1個の電気量は-e[C/個]なので、1秒間に導体の断面を通過する電気量は、
\begin{eqnarray}
-e{\mathrm{[C/個]}}×nvS{\mathrm{[個]}}=-envS{\mathrm{[C]}}
\end{eqnarray}
となります。
⑤電流の大きさの式『I=envS』が完成!

この電流の大きさついては以下のように定義されています。
つまり、電流の大きさIは
\begin{eqnarray}
I=|-e|nvS=envS
\end{eqnarray}
となります。求めるのは電流の大きさですから、電気量の絶対値|-e|=eを使うことに注意してください。
また、この自由電子の流れる向きが左向きに移動しているとすれば、電流の流れる向きは自由電子の流れる向きと逆のため、右向きに流れているということになります。
『I=envS』の覚え方
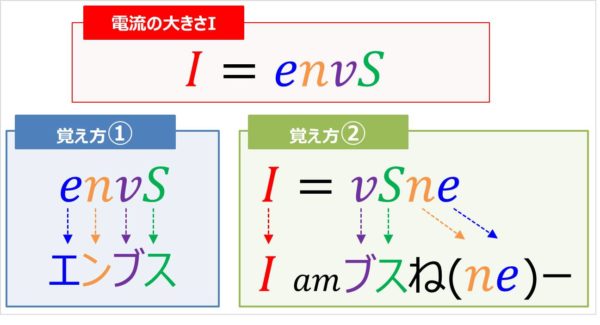
『I=envS』は有名な式なので様々な覚え方があります。
覚え方①:エンブス!
右辺の『envS』をそのまま『エンブス』と覚えます。この覚え方が一番オススメです。
なぜかというと、自由電子1個の電気量の大きさe[C/個]を1秒間に導体の断面を通過する自由電子の数nvS[個]に掛けるという、『I=envS』の導出の流れを崩さないからです。
覚え方②:I am ブス ね
『I=envS』の右辺を並び替えると、『I=vSne』となります。
イコール(=)をbe動詞の「am」に置き換えると、なんとなく英語で『I am ブス ね』と読むことができますね。
覚え方③:単純にイー・エヌ・ブイ・エス
右辺の『envS』のアルファベットをそのまま読むと、『イー・エヌ・ブイ・エス』となります。『イー・エヌ・ブイ・エス』を繰り返し発していると、暗記することができいます。私はこの覚え方で覚えました。
『I=envS』と『I=ΔQ/Δt』の関係
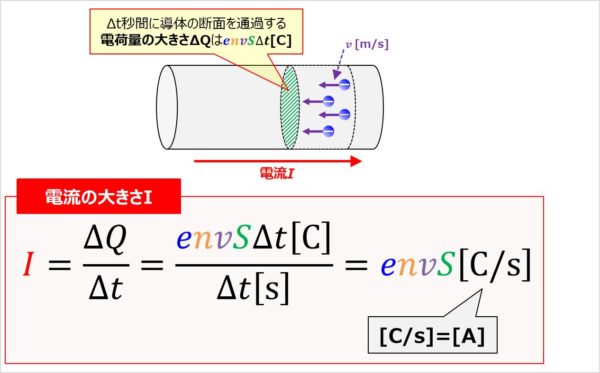
『I=envS』の導出方法において、先ほど、『1秒間に導体の断面を通過する電気量が-envS[C]なので、電流の大きさIがI=envSになる』と説明しました。
では、Δt秒間に導体の断面を通過する電気量の大きさΔQはどれくらいでしょうか。
1秒間で導体の断面を通過する電気量が『-envS[C]』なので、Δt秒間だと、
\begin{eqnarray}
{\Delta}Q=|-envS{\Delta}t|=envS{\Delta}t{\mathrm{[C]}}
\end{eqnarray}
となります。なお、電気量の大きさなので、絶対値を使っています。
上式を電流の有名な公式の1つである
\begin{eqnarray}
I=\frac{{\Delta}Q}{{\Delta}t}
\end{eqnarray}
に代入すると、
\begin{eqnarray}
I=\frac{{\Delta}Q}{{\Delta}t}=\frac{envS{\Delta}t}{{\Delta}t}=envS
\end{eqnarray}
となります。つまり、『I=ΔQ/Δt』と『I=envS』が同じということが分かりますね。この『I=envS』は電流を自由電子の動きを追うミクロな視点で考えた時の式となっています。
まとめ
この記事では『電流の大きさI=envS』について、以下の内容を説明しました。
当記事のまとめ
- 『I=envS』の公式
- 『I=envS』の導出
- 『I=envS』の覚え方
- 『I=envS』と『I=ΔQ/Δt』の関係
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






