コイルに流れる電流の位相が遅れる理由

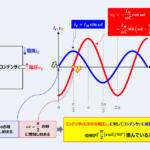
コイルに交流電圧を印加すると、コイルに流れる電流の位相が90度遅れます。

なぜ、電流の位相が90度遅れるのでしょうか。

この記事では、電流の位相が90度遅れる理由を『式』・『波形』・『覚え方』で説明します。

コイルに流れる電流の位相が遅れる理由

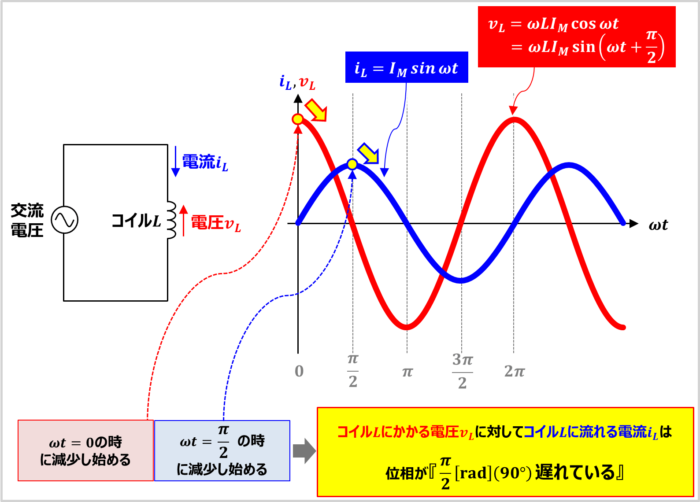
交流電圧にコイル\(L\)(自己インダクタンスを\(L{\mathrm{[H]}}\)とする)のみ接続した回路を上図に示しています。

コイル\(L\)に交流電圧を印加した時、次式で表される電流\(i_L\)がコイルに流れたとします。

\begin{eqnarray}
i_L=I_M{\sin}{\omega}t{\mathrm{[A]}}\tag{1}
\end{eqnarray}

この時、コイル\(L\)にかかる電圧\(v_L\)は次式で表されます。

\begin{eqnarray}
v_L&=&L×\frac{di_L}{dt}\\
&=&L×\frac{d}{dt}I_M{\sin}{\omega}t\\
&=&{\omega}LI_M{\cos}{\omega}t\\
&=&{\omega}LI_M{\sin}\left({\omega}t+\frac{{\pi}}{2}\right){\mathrm{[V]}}\tag{2}
\end{eqnarray}

(1)式と(2)式より、コイル\(L\)に流れる電流\(i_L\)とコイル\(L\)にかかる電圧\(v_L\)は上図に示すような波形となります。

コイル\(L\)に流れる電流\(i_L\)とコイル\(L\)にかかる電圧\(v_L\)の波形を見れば、位相の『進み』と『遅れ』を簡単に見分けることができます。

コイル\(L\)にかかる電圧\(v_L\)は\({\omega}t=0{\mathrm{[rad]}}\)の時に減少し始めます。

一方、コイル\(L\)に流れる電流\(i_L\)は\({\omega}t=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)の時に減少し始めます。

そのため、コイル\(L\)にかかる電圧\(v_L\)に対してコイル\(L\)に流れる電流\(i_L\)は位相が90度\((=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}})\)遅れていることが分かります。

補足

言い換えれば、コイル\(L\)に流れる電流\(i_L\)に対してコイル\(L\)にかかる電圧\(v_L\)は位相が90度\((=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}})\)進んでいるということになります。

コイルに流れる電流の『位相の覚え方』

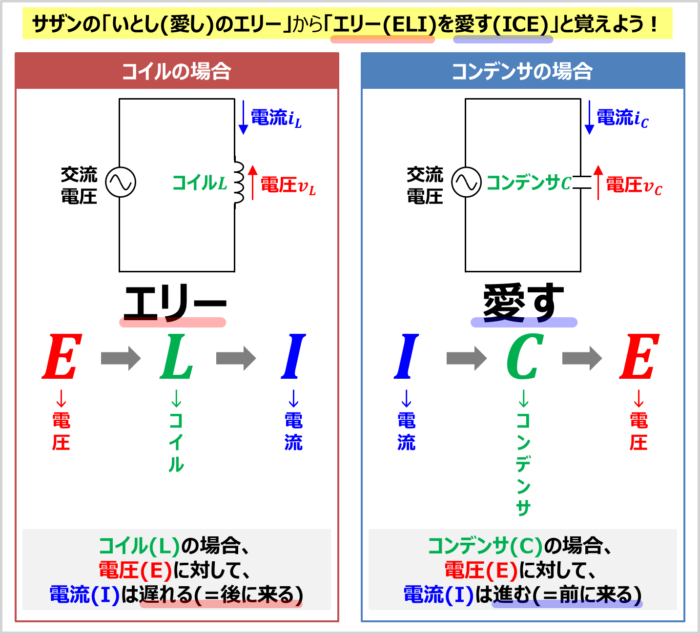
コイルに流れる電流の『位相の覚え方』としては、サザンオールスターズの「いとし(愛し)のエリー」から「エリー(ELI)を愛す(ICE)」と覚えましょう。

コイルの場合

コイル\(L\)に流れる電流\(i_L\)とコイル\(L\)にかかる電圧\(v_L\)の位相関係は「エリー(ELI)」となります。

「エリー(ELI)」のE、L、Iは以下の意味を表します。

E：電圧
L：コイル
I：電流

E(電圧)→L(コイル)→I(電流)の順番となっていますね。

そのため、『コイル(L)の場合、電圧(E)に対して、電流(I)は遅れる(=後に来る)』と覚えることができます。

コンデンサの場合

ついでに、コンデンサに流れる電流の『位相の覚え方』も説明します。

コンデンサ\(C\)に流れる電流\(i_C\)とコンデンサ\(C\)にかかる電圧\(v_C\)の位相関係は「愛す(ICE)」となります。

「愛す(ICE)」のI、C、Eは以下の意味を表します。

I：電流
C：コンデンサ
E：電圧

I(電流)→C(コンデンサ)→E(電圧)の順番となっていますね。

そのため、『コンデンサ(C)の場合、電圧(E)に対して、電流(I)は進む(=前に来る)』と覚えることができます。

コイルの特性から電流と電圧の位相関係を考えてみよう

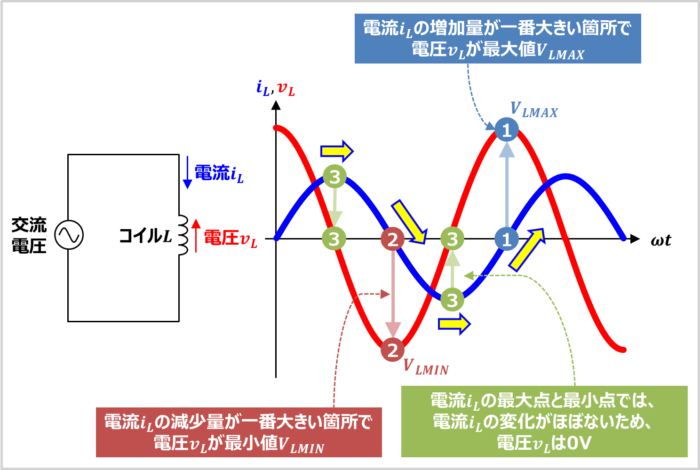
先ほど、(1)式と(2)式からコイル\(L\)に流れる電流\(i_L\)とコイル\(L\)にかかる電圧\(v_L\)の波形をプロットしましたが、コイルの特性を理解していれば、波形と簡単に描くことができます。

まず、コイル\(L\)に流れる電流\(i_L\)を正弦波でプロットします。

コイル\(L\)は電流\(i_L\)の変化を妨げる方向に電圧\(v_L\)が生じる特性があります。

そのため、下記のように電圧\(v_L\)の波形をプロットすることができます。

電流\(i_L\)の増加量が一番大きい箇所で電圧\(v_L\)が最大値\(V_{LMAX}\)
電流\(i_L\)の減少量が一番大きい箇所で電圧\(v_L\)が最小値\(V_{LMIN}\)
電流\(i_L\)の最大点と最小点では、電流\(i_L\)の変化がほぼないため、電圧\(v_L\)は0V

すると、コイル\(L\)に流れる電流\(i_L\)とコイル\(L\)にかかる電圧\(v_L\)の波形は上図に示すようになり、コイル\(L\)にかかる電圧\(v_L\)に対してコイル\(L\)に流れる電流\(i_L\)は位相が90度\((=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}})\)遅れていることが分かります。