この記事では『コンデンサに蓄えられるエネルギー』について
- 『コンデンサに蓄えられるエネルギー』の式と求め方
- 『コイルに蓄えられるエネルギー』との関係
などを図を用いて分かりやすく説明しています。
コンデンサに蓄えられるエネルギー

静電容量(キャパシタンス)がC[F]のコンデンサにV[V]の電圧がかかっている時、コンデンサに蓄えられるエネルギーU[J]は次式で表されます。
コンデンサに蓄えられるエネルギー
\begin{eqnarray}
U=\frac{1}{2}CV^2{\mathrm{[J]}}
\end{eqnarray}
U[J]:コンデンサに蓄えられるエネルギー
C[F]:コンデンサの静電容量
V[V]:コンデンサにかかっている電圧
単位は[J](ジュール)となります。次に上式の求め方について説明します。
補足
- コンデンサに蓄えられるエネルギーの記号には「U」ではなく下記式のように「W」を用いる場合もあります。
\begin{eqnarray}
W=\frac{1}{2}CV^2{\mathrm{[J]}}
\end{eqnarray}
コンデンサに蓄えられるエネルギーの求め方
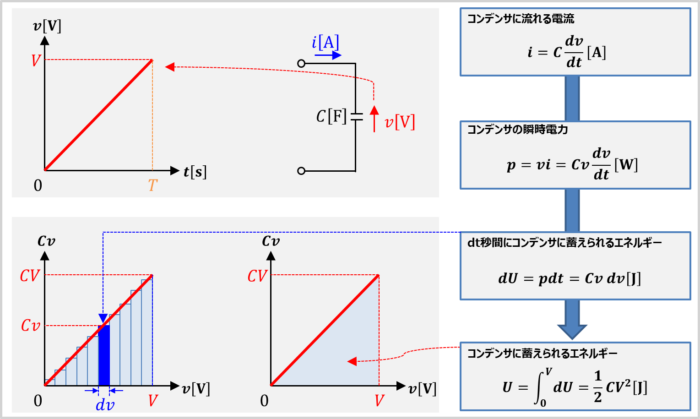
導出を簡単にするために、以下のようにコンデンサにかかる電圧vが変化した場合を考えます。
- t=0[s]の時:v=0[V]
- t=T[s]の時:v=V[V]
静電容量C[F]のコンデンサに電圧v[V]がかかっている時、dt秒間においてコンデンサにかかる電圧v[V]がdV[V]だけ変化すると、コンデンサに流れる電流i[A]は次式で表されます。
\begin{eqnarray}
i=C\frac{dv}{dt}{\mathrm{[V]}}
\end{eqnarray}
したがって、コンデンサに生じる瞬時電力p[W]は次式で表されます。
\begin{eqnarray}
p=vi=v×C\frac{dv}{dt}=Cv\frac{dv}{dt}
\end{eqnarray}
電力に時間を掛けるとエネルギーとなります。そのため、コンデンサがdt秒間に(コンデンサにかかる電圧がdv[V]変化した時に)蓄えられるエネルギーdU[J]は次式で表されます。
\begin{eqnarray}
dU=p×dt=Cv\frac{dv}{dt}×dt=Cv{\;}dv
\end{eqnarray}
上式はグラフでいうと青色の部分の面積となります。したがって、コンデンサにかかる電圧vが0[V]からV[V]まで増加した時、コンデンサに蓄えられるエネルギーU[J}は次式となります。
\begin{eqnarray}
U={\displaystyle\int}_0^V dU={\displaystyle\int}_0^V Cv{\;}dv=C{\displaystyle\int}_0^V v{\;}dv=C\left[\frac{1}{2}v^2\right]_0^V=\frac{1}{2}CV^2{\mathrm{[J]}}
\end{eqnarray}
上式はグラフでいると、三角形の面積となります。このようにしてコンデンサに蓄えられるエネルギーを求めます。
『コンデンサに蓄えられるエネルギー』と『コイルに蓄えられるエネルギー』の関係
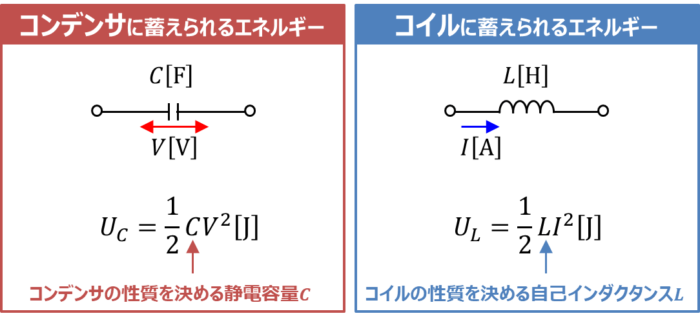
『コンデンサに蓄えられるエネルギーUC』と『コイルに蓄えられるエネルギーUL』の式は似ています。下記に各エネルギーの式を示します。
\begin{eqnarray}
U_C&=&\frac{1}{2}CV^2{\mathrm{[J]}}\\
U_L&=&\frac{1}{2}LI^2{\mathrm{[J]}}
\end{eqnarray}
コンデンサは電圧がかかることでエネルギーが蓄えられるので、式に電圧のVが付いています。一方、コイルは電流が流れることでエネルギーが蓄えられるので、式に電流のIが付いています。
また『コンデンサの性質を決める静電容量C』と『コイルの性質を決める自己インダクタンスL』がそれぞれの式に付いています。
このように式を並べると似ていることが分かります。なお、コンデンサに蓄えられるエネルギーには「静電エネルギー」という名前が付けられていますが、コイルに蓄えられるエネルギーには特に名前が付けられていません。
まとめ
この記事では『コンデンサに蓄えられるエネルギー』について、以下の内容を説明しました。
- 『コンデンサに蓄えられるエネルギー』の式と求め方
- 『コイルに蓄えられるエネルギー』との関係
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






