【昇圧コンバータの設計】出力コンデンサのESRによるリプルの導出

この記事では『昇圧コンバータ』において

などを図を用いて分かりやすく説明しています。

出力コンデンサのESRによるリプルについて

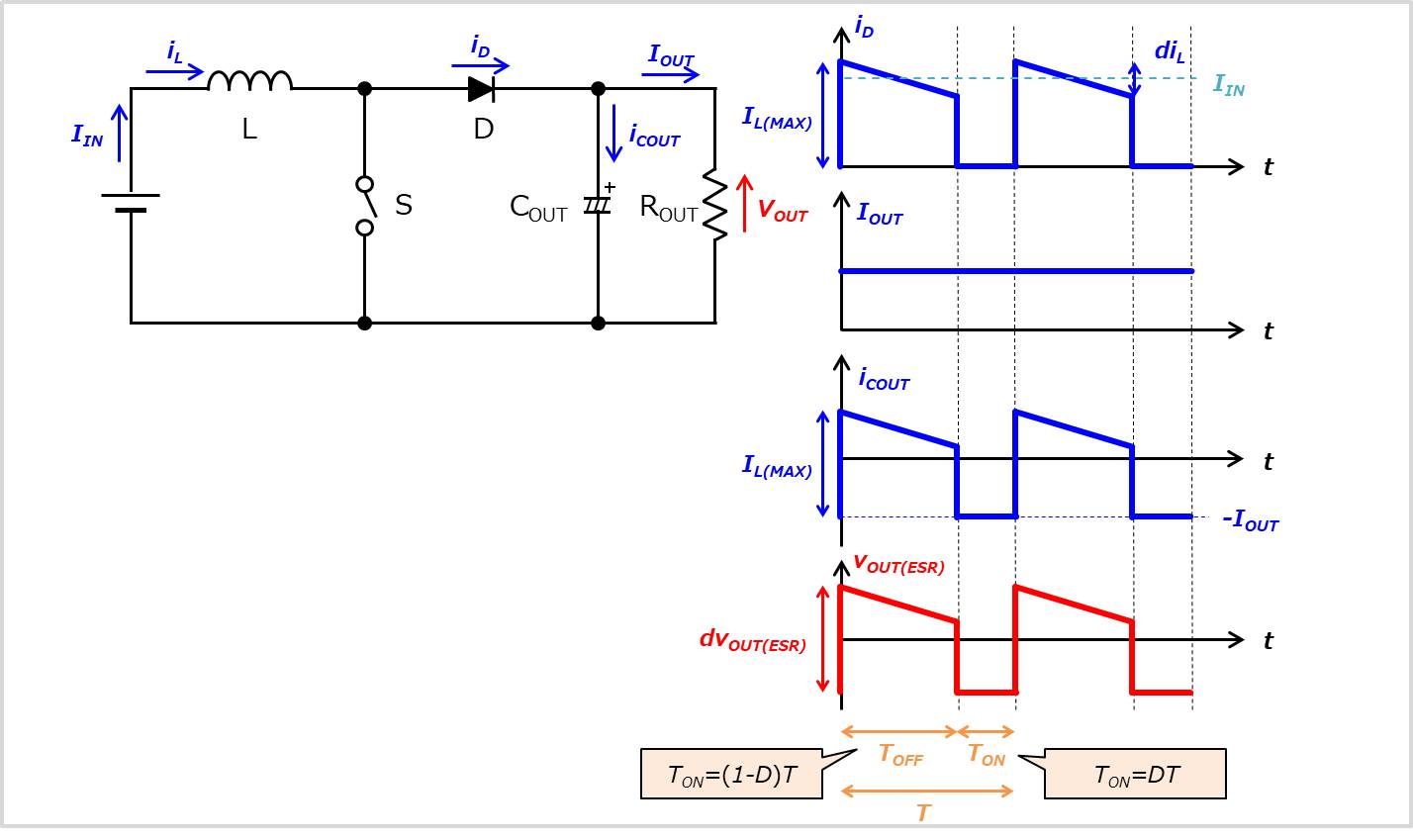
出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)により、出力電圧\(V_{OUT}\)にリプルが生じます。

この出力電圧\(V_{OUT}\)のリプルには、出力コンデンサの充放電によって生じるリプル\(dV_{OUT}\)以外にも出力コンデンサ\(C_{OUT}\)の等価直列抵抗(ESR)によって生じるリプル\(dV_{OUT(ESR)}\)があります。

実際のリプルは\(dV_{OUT}\)と\(dV_{OUT(ESR)}\)が合わさったものとなっています。

ではこれから、出力コンデンサ\(C_{OUT}\)のESRによって生じるリプル\(dV_{OUT(ESR)}\)の大きさと計算方法について説明します。

出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は回路図より、ダイオード\(D\)に流れる電流\(i_{D}\)と出力電流\(I_{OUT}\)の差分になっています。スイッチ\(S\)のオン時はダイオード\(D\)に電流が流れないため、出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は
\begin{eqnarray}
i_{COUT}= -I_{OUT}\tag{1}
\end{eqnarray}
となります。スイッチ\(S\)のオフ時はダイオード\(D\)に電流\(i_{D}\)が流れているため、出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は
\begin{eqnarray}
i_{COUT}= i_{D}-I_{OUT}\tag{2}
\end{eqnarray}

となります。

また、ダイオード\(D\)に流れる電流\(i_{D}\)の最大値はインダクタ\(L\)に流れる電流\(i_{L}\)のピーク値\(I_{L(MAX)}\)と等しくなるため、出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)のリプルはインダクタ\(L\)に流れる電流\(i_{L}\)のピーク値\(I_{L(MAX)}\)と等しくなります(グラフから考えるとわかりやすいと思います)。

そのため、出力コンデンサ\(C_{OUT}\)のESRによって生じるリプル\(dV_{OUT(ESR)}\)は

となります。
インダクタ電流\(i_{L}\)のピーク値\(I_{L(MAX)}\)は入力電流\(I_{IN}\)を用いると以下の式となります。
\begin{eqnarray}
I_{L(MAX)}= \frac{1}{2}di_{L}+ I_{IN}\tag{4}
\end{eqnarray}

そのため、(3)式は以下の式となります。

さらに、入力電流\(I_{IN}\)は出力電流\(I_{OUT}\)とオンデューティ\(D\)を用いると以下の式となります。
\begin{eqnarray}
I_{IN}= \frac{ I_{OUT}}{1-D}\tag{6}
\end{eqnarray}

そのため、(5)式は以下の式となります。