【昇圧コンバータの設計】出力コンデンサに流れる電流の実効値(RMS)の計算

この記事では『昇圧コンバータ』において

などを図を用いて分かりやすく説明しています。

出力コンデンサに流れる電流の実効値(RMS)の計算方法と式

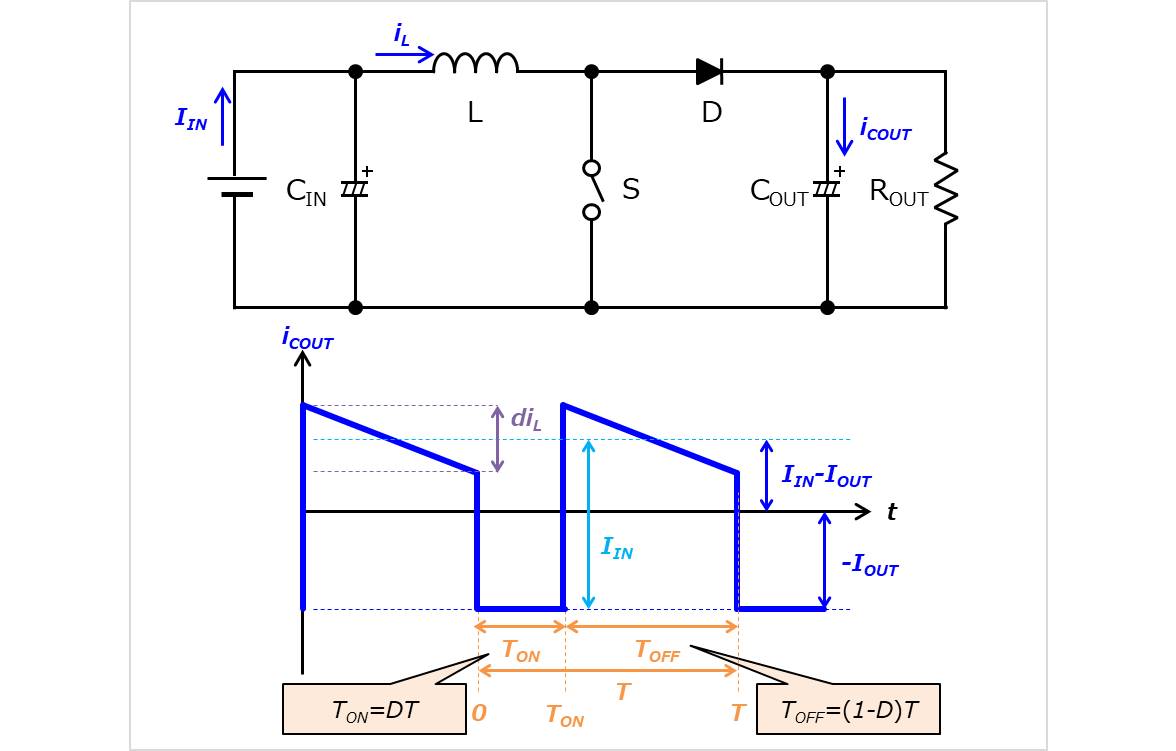
出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は上図のようになります。電流\(i_{COUT}\)の実効値\(i_{COUT(RMS)}\)を導出する前に、以下の式をあらかじめ使用します。

電流\(i_{COUT}\)の実効値\(i_{COUT(RMS)}\)はスイッチのオン時間を\(T_{ON}\)、オフ時間を\(T_{OFF}\)とすると、
\begin{eqnarray}
i_{COUT(RMS)}&=&\sqrt{\frac{1}{T}\displaystyle\int_{0}^{T}{ i_{COUT}}^2dt}\\
&=&\sqrt{\frac{1}{T}\displaystyle\int_{0}^{T_{ON}}{ i_{COUT}}^2dt+\frac{1}{T}\displaystyle\int_{ T_{ON}}^{T}{ i_{COUT}}^2dt}
\end{eqnarray}
となります。ここで、式が複雑になるので、以下のように\(A\)と\(B\)で分けて計算を行います。
\begin{eqnarray}
A&=&\frac{1}{T}\displaystyle\int_{0}^{T_{ON}}{ i_{COUT}}^2dt\\
B&=&\frac{1}{T}\displaystyle\int_{ T_{ON}}^{T}{ i_{COUT}}^2dt\\
i_{COUT(RMS)}&=&\sqrt{A+B}
\end{eqnarray}

まず\(A\)から計算します。期間\(0\)～\(T_{ON}\)では出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は\({-I_{OUT}}\)となります。そのため、
\begin{eqnarray}
A&=&\frac{1}{T}\displaystyle\int_{0}^{T_{ON}}{i_{COUT}}^2dt\\
&=&\frac{ T_{ON}}{T}(-I_{OUT})^2\\
&=&D{I_{OUT}}^2
\end{eqnarray}

次に\(B\)を計算します。期間\(T_{ON}\)～\(T\)では出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)は台形波となっています。台形波は入力電流\(I_{IN}\)と出力電流\(I_{OUT}\)の差分に対して、リプル\(di_{L}\)が合わさった波形となっています。そのため、
\begin{eqnarray}
B&=&\frac{1}{T}\displaystyle\int_{T_{ON}}^{T}{i_{COUT}}^2dt\\
&=&\frac{T-T_{ON}}{T}×\left(\left (I_{IN}-I_{OUT}\right)^2+\frac{1}{12}{di_{L}}^2\right)\\
&=&(1-D)×\left(\left (\frac{I_{OUT}}{1-D}-I_{OUT}\right)^2+\frac{1}{12}{di_{L}}^2\right)\\
&=&(1-D)×\left(\left (\frac{DI_{OUT}}{1-D}\right)^2+\frac{1}{12}{di_{L}}^2\right)
\end{eqnarray}
なお、台形波の実行値の求め方は以下の記事に詳しく説明しています。
『台形波』の実効値・平均値の求め方

したがって、出力コンデンサ\(C_{OUT}\)に流れる電流\(i_{COUT}\)の実効値\(i_{COUT(RMS)}\)は、

となります。