昇圧チョッパ(ブーストコンバータ、ステップ・アップ・コンバータ)において、入力コンデンサの容量値の設計方法について説明します。
『入力コンデンサ』の設計方法
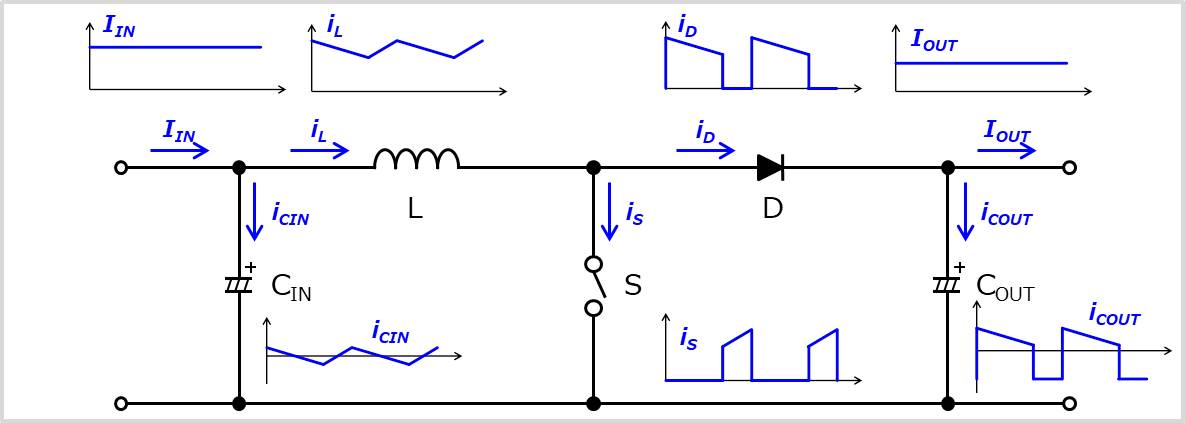
昇圧チョッパの各電流波形は上図のようになっています。
ここで、入力電流IIN、インダクタLに流れる電流iL、入力コンデンサCINに流れる電流iCINの電流波形と、入力電圧vINの電圧波形は下図のようになっています。
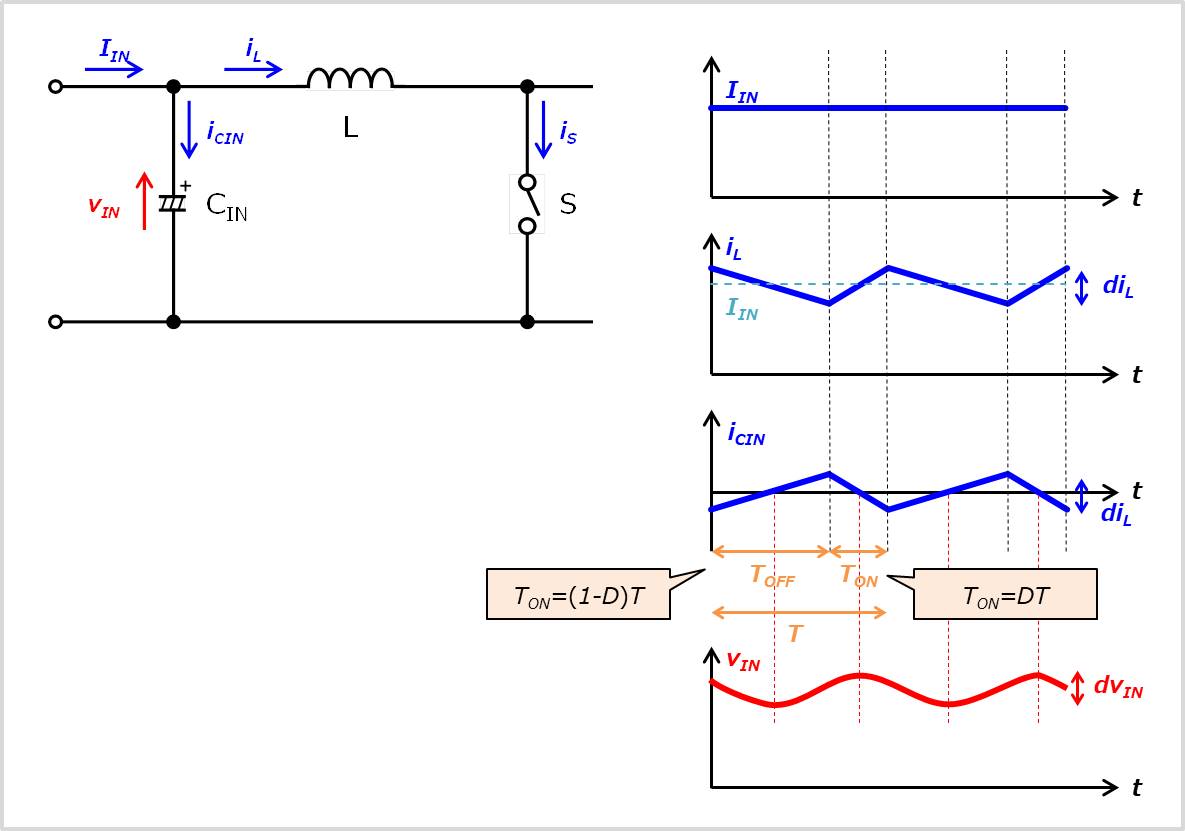
スイッチSがオンの期間においてはインダクタ電流iLが増加し、スイッチSがオフの期間においてはインダクタ電流iLが減少するため、インダクタ電流iLにはリプルdiLが生じます。
- インダクタ電流iLが入力電流IINより大きい期間
- インダクタ電流iLが入力電流IINより小さい期間
入力コンデンサCINから電流が流れるので、入力電圧vINは減少します。
入力コンデンサCINに電流が流れるので、入力電圧vINが増加します。
このように、入力コンデンサCINに流れる電流iCINにより、入力電圧vINにリプルdVINが生じます。
下図に入力コンデンサCINに流れる電流iCINの電流波形の拡大図を示します。
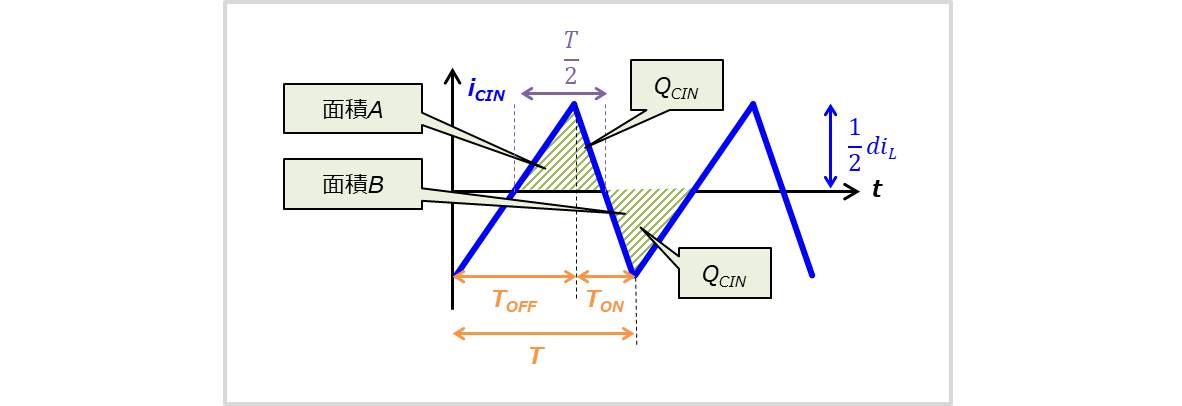
入力電圧vINを一定に保つためには、入力コンデンサの充電電荷量(面積A)と放電電荷量(面積B)が等しくなる必要があります。
今回、面積Aに焦点を当てて入力コンデンサの設計を行います。
充電電荷量をQCIN、入力コンデンサのキャパシタンスをCINとすると、入力コンデンサCINにQCINの電荷が充電されることで、入力電圧vINがdVIN増加するので、
\begin{eqnarray}
Q_{CIN}=C_{IN}dv_{IN}
\end{eqnarray}
となります。
また、コンデンサに流れる電流iCINを積分したものが充電電荷量QCINであるため、
\begin{eqnarray}
Q_{CIN}=\frac{1}{2}×\frac{1}{2}T×\frac{1}{2}di_L=\frac{1}{8}Tdi_L
\end{eqnarray}
となります。
したがって、
\begin{eqnarray}
C_{IN}dv_{IN}=\frac{1}{8}Tdi_L{\Leftrightarrow}C_{IN}=\frac{1}{8dv_{IN}}Tdi_L
\end{eqnarray}
となります。
周期Tと周波数fSWの関係式
\begin{eqnarray}
T=\frac{1}{f_{SW}}
\end{eqnarray}
を用いると、以下の式に変換することができます。
\begin{eqnarray}
C_{IN}=\frac{di_L}{8f_{SW}dv_{IN}}
\end{eqnarray}
設計においては、インダクタ電流のリプルdiLと電圧リプルdvINを設計し、そこで求めた入力コンデンサの容量値CINより大きな値を選定するようにするため、
C_{IN}>\frac{di_L}{8f_{SW}dv_{IN}}
\end{eqnarray}
となります。
なお、入力電流IINのリプル率をkとすると、
\begin{eqnarray}
di_L=kI_{IN}
\end{eqnarray}
となります。
したがって、
C_{IN}>\frac{kI_{IN}}{8f_{SW}dv_{IN}}
\end{eqnarray}
となります。
出力電流IOUTと入力電流IINの関係式
\begin{eqnarray}
I_{OUT}=(1-D)I_{IN}
\end{eqnarray}
を用いると、
C_{IN}>\frac{kI_{OUT}}{8f_{SW}dv_{IN}(1-D)}
\end{eqnarray}
となります。






