この記事ではアンペアの周回積分の法則について
- 『アンペアの周回積分の法則』とは
- 『アンペアの周回積分の法則』を用いて磁界の強さHを導出する方法
- 『アンペアの周回積分の法則』に関する問題
などを図を用いて分かりやすく説明しています。
『アンペアの周回積分の法則』とは
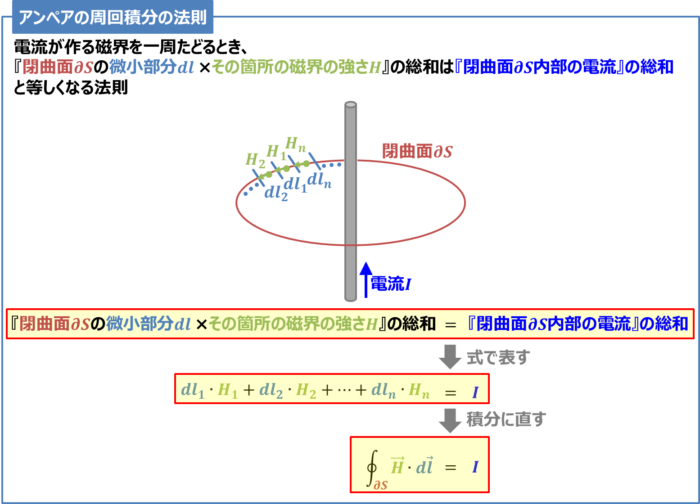
アンペアの周回積分の法則とは、電流が作る磁界を一周たどるとき、『閉曲面の微小部分×その箇所の磁界の強さ』の総和は『閉曲面内部の電流』の総和と等しくなる法則です。アンペアの周回積分の法則は『アンペアの周回路の法則』とも呼ばれています。
もう少し詳しく説明します。
上図に示すように、\(1\)本の電線に電流\(I{\mathrm{[A]}}\)が流れると、その周囲には磁界が発生します。
ここで、閉曲面\({{\partial}S}\)を微小部分\(dl_1,dl_2,{\;}{\cdots}{\;},dl_n{\mathrm{[m]}}\)と分けます。
また、その箇所の磁界の強さを\(H_1,H_2,{\;}{\cdots}{\;},H_n{\mathrm{[A/m]}}\)とします。
その時、『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和は『閉曲面\({{\partial}S}\)内部の電流』の総和(上図では\(I{\mathrm{[A]}}\))と等しくなります。
式で表すと、次式で表すことができます。
\begin{eqnarray}
{dl_1}{\;}{\cdot}{\;}{H_1}+{dl_2}{\;}{\cdot}{\;}{H_2}+{\;}{\cdots}{\;}+{dl_n}{\;}{\cdot}{\;}{H_n}=I\tag{1}
\end{eqnarray}
ここで、左辺を積分に直すと、次式に変換することができます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=I\tag{2}
\end{eqnarray}
上式は『磁界を周回積分すると、その中を流れる電流に等しい』ということを示しています。
アンペアの周回積分の法則の閉曲面は『円』である必要はありません。あらゆる閉曲面で成り立ちます。楕円形でも四角形でも閉曲面であれば、閉曲面を微小部分\(dl\)に分け、その箇所の磁界の強さ\(H\)を求め、それを積分することで、磁界の強さ\(H\)を求めることができます。
補足
電流密度\(J\)を用いると、『閉曲面\({{\partial}S}\)内部の電流』の総和は\({\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\)で表すことができるため、(2)式は次式で表すことができます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}={\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\tag{3}
\end{eqnarray}
『アンペアの周回積分の法則』を用いて磁界の強さHを導出する方法
次に、アンペアの周回積分の法則を用いて
- 直流導体\(1\)本の周囲の磁界の強さ\(H\)の導出
- 直流導体\(N\)本の周囲の磁界の強さ\(H\)の導出
- 環状ソレノイドの磁界の強さ\(H\)の導出
の磁界の強さ\(H\)を導出する方法を説明します。磁界の強さ\(H\)は以下の流れによって導出することができます。
磁界の強さを求める方法
- 『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和\(\left({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\right)\)を求める
- 『閉曲面\({{\partial}S}\)内部の電流』の総和\(\left({\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\right)\)を求める
- ①と②を『イコール(\(=\))』で結ぶ
直流導体1本の周囲の磁界の強さHの導出
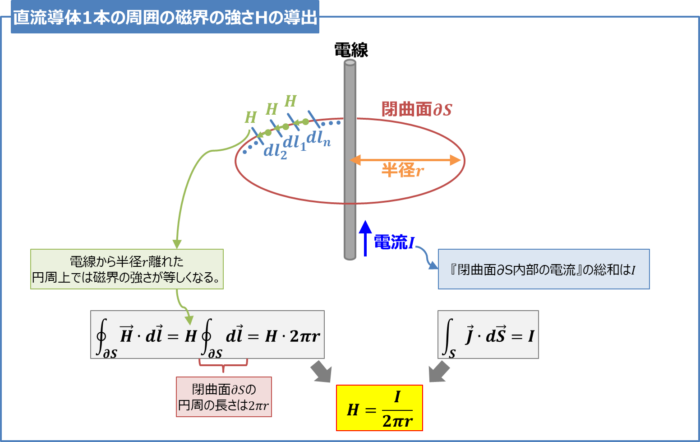
\(1\)本の電線に電流\(I{\mathrm{[A]}}\)が流れるとき、電線から半径\(r{\mathrm{[m]}}\)離れた点の磁界の強さ\(H{\mathrm{[A/m]}}\)をアンペアの周回積分の法則を用いて導出してみましょう。
step
1『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和を求める
電線から半径\(r{\mathrm{[m]}}\)離れた円周上では磁界の強さが等しくなります。そのため、積分記号『\({\displaystyle\oint}\)』の外に出すことができます。ここで、この磁界の強さを\(H{\mathrm{[A/m]}}\)とすると、『\({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\)』は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\displaystyle\oint}_{{\partial}S}d{\vec{l}}\tag{4}
\end{eqnarray}
また、『\({\displaystyle\oint}_{{\partial}S}d{\vec{l}}\)』は半径\(r{\mathrm{[m]}}\)の円周の長さであるため、次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}d{\vec{l}}=2{\pi}r\tag{5}
\end{eqnarray}
(5)式を(4)式に代入すると、『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和\(\left({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\right)\)は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\;}{\cdot}{\;}2{\pi}r\tag{6}
\end{eqnarray}
『\({\displaystyle\oint}_{{\partial}S}d{\vec{l}}\)』は周回積分と呼ばれるものであり、閉曲面\({{\partial}S}\)を微小部分\(d{\vec{l}}\)に分け、それらを全て足したものです。
step
2『閉曲面\({{\partial}S}\)内部の電流』の総和を求める
『閉曲面\({{\partial}S}\)内部の電流』の総和は\(I{\mathrm{[A]}}\)なので次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}=I\tag{7}
\end{eqnarray}
step
3①と②を『イコール(\(=\))』で結ぶ
(6)式と(7)式を(3)式に代入すると次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}&=&{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\\
{\Leftrightarrow}H{\;}{\cdot}{\;}2{\pi}r&=&I\\
H&=&\frac{I}{2{\pi}r}\tag{8}
\end{eqnarray}
ゆえに、(8)式より\(1\)本の電線に電流\(I{\mathrm{[A]}}\)が流れるとき、電線から半径\(r{\mathrm{[m]}}\)離れた点の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式となります。
\begin{eqnarray}
H&=&\frac{I}{2{\pi}r}
\end{eqnarray}
あわせて読みたい
磁界の強さ\(H{\mathrm{[A/m]}}\)は『ビオ・サバールの法則』でも求めることができます。『ビオ・サバールの法則』について以下の記事で説明していますので、参考にしてください。
-

【ビオ・サバールの法則とは】『直流電流』や『円電流』の磁界の強さの導出など!
続きを見る
直流導体N本の周囲の磁界の強さHの導出
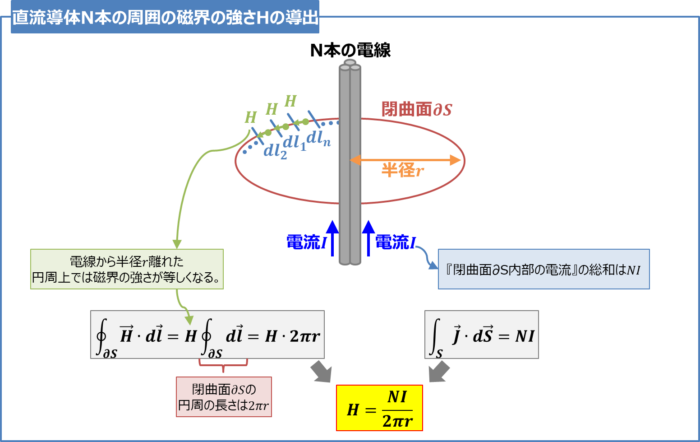

\(N\)本の電線に電流\(I{\mathrm{[A]}}\)が流れるとき、電線から半径\(r{\mathrm{[m]}}\)離れた点の磁界の強さ\(H{\mathrm{[A/m]}}\)をアンペアの周回積分の法則を用いて導出してみましょう。
step
1『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和を求める
電線から半径\(r{\mathrm{[m]}}\)離れた円周上では磁界の強さが等しくなります。そのため、積分記号『\({\displaystyle\oint}\)』の外に出すことができます。ここで、この磁界の強さを\(H{\mathrm{[A/m]}}\)とすると、『\({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\)』は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\displaystyle\oint}_{{\partial}S}d{\vec{l}}\tag{9}
\end{eqnarray}
また、『\({\displaystyle\oint}_{{\partial}S}d{\vec{l}}\)』は半径\(r{\mathrm{[m]}}\)の円周の長さであるため、次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}d{\vec{l}}=2{\pi}r\tag{10}
\end{eqnarray}
(10)式を(9)式に代入すると、『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和\(\left({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\right)\)は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\;}{\cdot}{\;}2{\pi}r\tag{11}
\end{eqnarray}
ここまでは、先ほど導出した『直流導体\(1\)本の周囲の磁界の強さ\(H\)の導出』の流れと同じです。
step
2『閉曲面\({{\partial}S}\)内部の電流』の総和を求める
『閉曲面\({{\partial}S}\)内部の電流』の総和は\(NI{\mathrm{[A]}}\)なので次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}=NI\tag{12}
\end{eqnarray}
step
3①と②を『イコール(\(=\))』で結ぶ
(11)式と(12)式を(3)式に代入すると次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}&=&{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\\
{\Leftrightarrow}H{\;}{\cdot}{\;}2{\pi}r&=&NI\\
H&=&\frac{NI}{2{\pi}r}\tag{13}
\end{eqnarray}
ゆえに、(13)式より\(N\)本の電線に電流\(I{\mathrm{[A]}}\)が流れるとき、電線から半径\(r{\mathrm{[m]}}\)離れた点の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式となります。
\begin{eqnarray}
H&=&\frac{NI}{2{\pi}r}
\end{eqnarray}
環状ソレノイドの磁界の強さHの導出
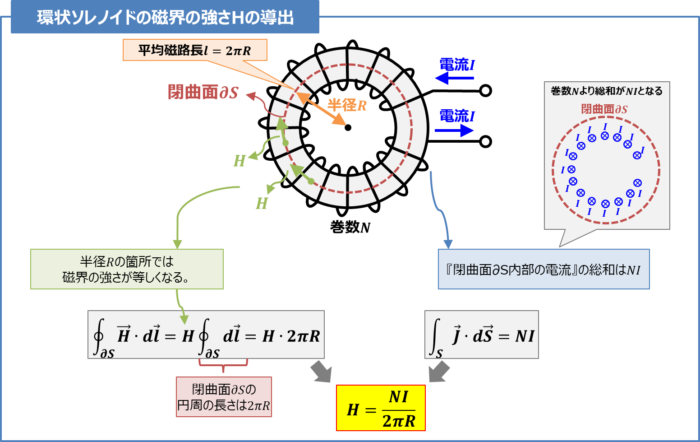

巻数\(N\)、平均半径\(R{\mathrm{[m]}}\)(平均磁路長\(l=2{\pi}R{\mathrm{[m]}}\))の環状ソレノイドに電流\(I{\mathrm{[A]}}\)が流れるとき、環状ソレノイド内部の磁界の強さ\(H{\mathrm{[A/m]}}\)をアンペアの周回積分の法則を用いて導出してみましょう。
step
1『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和を求める
平均半径\(R{\mathrm{[m]}}\)の箇所では磁界の強さが等しくなります。そのため、積分記号『\({\displaystyle\oint}\)』の外に出すことができます。ここで、この磁界の強さを\(H{\mathrm{[A/m]}}\)とすると、『\({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\)』は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\displaystyle\oint}_{{\partial}S}d{\vec{l}}\tag{14}
\end{eqnarray}
また、『\({\displaystyle\oint}_{{\partial}S}d{\vec{l}}\)』は半径\(R{\mathrm{[m]}}\)の円周の長さであるため、次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}d{\vec{l}}=2{\pi}R\tag{15}
\end{eqnarray}
(15)式を(14)式に代入すると、『閉曲面\({{\partial}S}\)の微小部分\(dl\)×その箇所の磁界の強さ\(H\)』の総和\(\left({\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}\right)\)は次式となります。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=H{\;}{\cdot}{\;}2{\pi}R\tag{16}
\end{eqnarray}
step
2『閉曲面\({{\partial}S}\)内部の電流』の総和を求める
『閉曲面\({{\partial}S}\)内部の電流』の総和は\(NI{\mathrm{[A]}}\)なので次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}=NI\tag{17}
\end{eqnarray}
step
3①と②を『イコール(\(=\))』で結ぶ
(16)式と(17)式を(3)式に代入すると次式が成り立ちます。
\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}&=&{\displaystyle\int}_{S}{\vec{J}}{\;}{\cdot}{\;}d{\vec{S}}\\
{\Leftrightarrow}H{\;}{\cdot}{\;}2{\pi}R&=&NI\\
H&=&\frac{NI}{2{\pi}R}\tag{17}
\end{eqnarray}
ゆえに、(17)式より巻数\(N\)、平均半径\(R{\mathrm{[m]}}\)(平均磁路長\(l=2{\pi}R{\mathrm{[A]}}\))の環状ソレノイドに電流\(I{\mathrm{[A]}}\)が流れるとき、環状ソレノイド内部の磁界の強さ\(H{\mathrm{[A/m]}}\)は次式となります。
\begin{eqnarray}
H&=&\frac{NI}{2{\pi}R}
\end{eqnarray}
『アンペアの周回積分の法則』に関する問題
問題文
\(3\)本の無限に長い電線に、それぞれ\(2{\mathrm{[A]}}\)の電流が流れている時、電線から\(20{\mathrm{[cm]}}\)離れた点での磁界の強さを求めてみましょう。
回答
半径\(r=20{\mathrm{[cm]}}=0.2{\mathrm{[m]}}\)であり、本数\(N=3\)なので、(13)式に代入すると、
\begin{eqnarray}
H&=&\frac{NI}{2{\pi}r}\\
&=&\frac{3×2}{2{\pi}×0.2}\\
&{\approx}&4.77{\mathrm{[A/m]}}
\end{eqnarray}
となります。
まとめ
この記事ではアンペアの周回積分の法則ついて、以下の内容を説明しました。
当記事のまとめ
- 『アンペアの周回積分の法則』とは
- 『アンペアの周回積分の法則』を用いて磁界の強さHを導出する方法
- 『アンペアの周回積分の法則』に関する問題
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。