この記事では『風量』と『風速』について
- 『風量』と『風速』の違い
- 『風量』と『風速』の計算式
- 『風量』と『風速』の単位
- 『風量』から『風速』、『風速』から『風量』を導出する計算例
を図を用いて説明しています。
『風量』と『風速』の違いと計算式について!
風の強さを表すものとして『風速』がありますが、似たような言葉に『風量』というものがあります。これらの違いをご存知でしょうか。
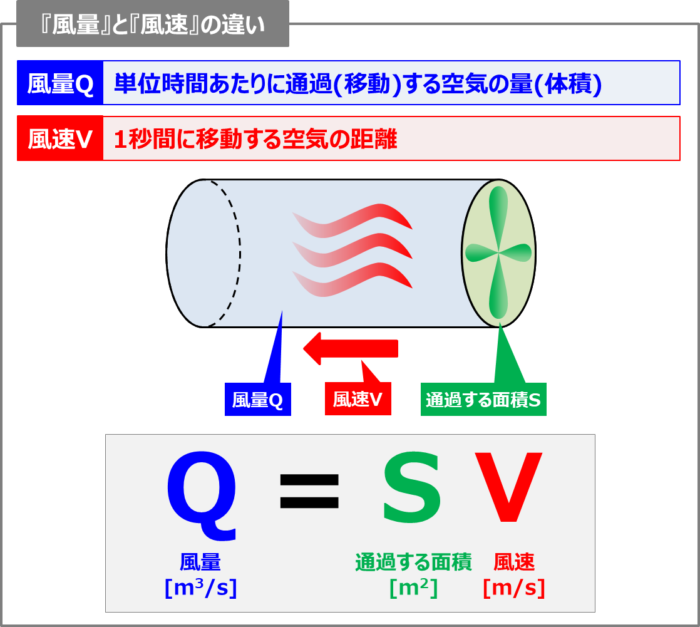
先に結論から言うと、風量は「単位時間あたりに通過(移動)する空気の量(体積)」を表し、風速は「1秒間に移動する空気の距離」を表しています。
図でイメージすると、「通過する面積S(緑色の部分)」×「風速V(赤色の部分)」が「風量Q(青色の部分)」となり、面積をS[m2]、風速をV[m/s]とすると、風量Q[m3/s]は次式で表されます。
風量と風速の計算式
\begin{eqnarray}
Q=SV
\end{eqnarray}
後ほど上式を用いて、『風量から風速を導出する計算例』と『風速から風量を導出する計算例』を解いていきますが、例題を解く際、『風量』と『風速』の単位を理解しておく必要があるので、次に単位について説明します。
風量の単位について
先ほど風量の単位は[m3/s]で表しましたが、風量の単位は様々あります。
例えば、[cm3/s],[m3/min],[cm3/min],[m3,h],[cm3/h]など使われることがあります。この中で一般的には[m3/min]と[m3/h]が多く用いられています。
例えば、風量Qが10[m3/min]だった場合、「1分間に通過する空気の量(体積)が10m3」ということを意味しています。
また、風量の単位にはCMMやCMHもあり、各単位は以下の意味となっています。
CMMとCMHの意味
- CMM:Cubic(立方) Meter(メートル) Minutes (時)を表しており、[m3/min]と同じです。
- CMH:Cubic(立方) Meter(メートル) Hour(時)を表しており、[m3/h]と同じです。
単位時間について
風量は「単位時間あたりに通過(移動)する空気の量(体積)」を表します。ここに出てくる単位時間とは「基準となる時間の長さのこと」を意味しており、単位における「/s」,「/min」,「/h」の部分となります。各単位時間は以下の意味をあらわしています。
- 「/s」:1秒間あたり
- 「/min」:1分間あたり
- 「/h」:1時間あたり
風速の単位について
風速の単位は[m/s]または[kn]で表します。[m/s]は「めーたーぱーせかんど、めーとるまいびょう」と読みます。[kn]は「ノット(knot)」と読みます。
例えば、風速が10[m/s]だった場合、「1秒間に空気が10m進む」ということを意味しています。
また、[kn]は「1時間に1海里(=1.852km)進む速さ」ということを意味しています。すなわち、[kn]と[m/s]は以下の関係式となります。
関係式
\begin{eqnarray}
1{\mathrm{[kn]}}&=&1{\mathrm{[海里/h]}}\\
&=&1{\mathrm{[海里/h]}}×1.852{\mathrm{[km/海里]}}\\
&=&1.852{\mathrm{[km/h]}}\\
&=&1.852{\mathrm{[km/h]}}×1000{\mathrm{[m/km]}}×\frac{1}{3600{\mathrm{[s/h]}}}\\
&=&0.514{\mathrm{[m/s]}}\\
\end{eqnarray}
補足
- 天気予報などでたまに聞く最大風速は10分間平均風速の最大値となっています。
- 風速の目安ですが風速が10[m/s]を超えると傘がさせず、15[m/s]を超えると転倒する人があらわれる強さです。また、風速が17.2[m/s]を超えると台風と定義されています。
『風速』から『風量』を導出する計算例
問題文
半径10cm(=0.1m)の円柱内部において風速V=5[m/s]の風が通過する場合の風量Qを求めてみましょう。

回答
step
1通過する面積Sを求める
半径10cm(=0.1m)の円柱の面積S[m2]は「半径×半径×3.14」より以下の値となります。
\begin{eqnarray}
S=0.1×0.1×3.14=0.0314{\mathrm{[m^2]}}
\end{eqnarray}
step
2面積Sに風速Vをかけて風量Qを求める
面積S[m2]に風速V[m/s]をかけることで風量Qを求めることができます。
\begin{eqnarray}
Q=SV=0.0314{\mathrm{[m^2]}}×5{\mathrm{[m/s]}}=0.157{\mathrm{[m^3/s]}}
\end{eqnarray}
step
3風速の単位を変える
風速の単位を[m3/min]や[m3/h]を変えたい場合には単位変換を行います。
- 単位を[m3/min]に変える場合
- 単位を[m3/h]に変える場合
1分間は60秒なので60[s/min]をかけることで単位変換できます。
\begin{eqnarray}
0.157{\mathrm{[m^3/s]}}×60{\mathrm{[s/min]}}=9.42{\mathrm{[m^3/min]}}
\end{eqnarray}
1時間は3600秒なので3600[s/h]をかけることで単位変換できます。
\begin{eqnarray}
0.157{\mathrm{[m^3/s]}}×3600{\mathrm{[s/h]}}=565.2{\mathrm{[m^3/h]}}
\end{eqnarray}
『風量』から『風速』を導出する計算例
問題文
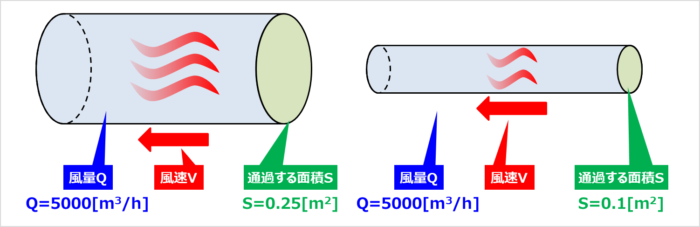
風量Q=5000[m3/h]において、面積がS=0.25[m2]の時とS=0.01[m2]の時における風速Vを求めてみましょう。
step
1風量Qの単位を変える
風量の単位の「/h」を「/s」に変えます。
1時間は3600秒なので3600[s/h]を割ることで単位変換できます。
\begin{eqnarray}
Q=5000{\mathrm{[m^3/h]}}×\frac{1}{3600{\mathrm{[s/h]}}}=1.388{\mathrm{[m^3/s]}}
\end{eqnarray}
step
2風量Qを面積Sで割って風速を求める
- 面積がS=0.25[m2]の時
- 面積がS=0.01[m2]の時
\begin{eqnarray}
V=\frac{Q}{S}=\frac{1.388{\mathrm{[m^3/s]}}}{0.25{\mathrm{[m^2]}}}=5.55{\mathrm{[m/s]}}
\end{eqnarray}
\begin{eqnarray}
V=\frac{Q}{S}=\frac{1.388{\mathrm{[m^3/s]}}}{0.01{\mathrm{[m^2]}}}=138.8{\mathrm{[m/s]}}
\end{eqnarray}
このように面積が小さくなると風速が速くなることが分かります。『太いストローをくわえて息を吐いたとき』と『細いストローをくわえて息を吐いたとき』では細いストローの方が勢いよく息が出てくることからイメージが湧くと思います。
まとめ
この記事では『風量』と『風速』ついて、以下の内容を説明しました。
当記事のまとめ
- 『風量』と『風速』の違い
- 『風量』と『風速』の計算式
- 『風量』と『風速』の単位
- 『風量』から『風速』、『風速』から『風量』を導出する計算例
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






