『加算回路』を分かりやすく解説！【オペアンプ】

この記事では『加算回路』において

などを図を用いて分かりやすく説明しています。

加算回路の式

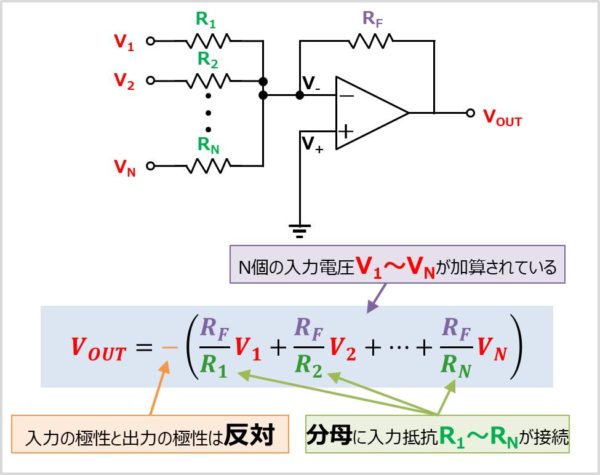
上図に加算回路(Adder Circuit)の式を示します。加算回路には\(N\)個の入力電圧\(V_{1}\)～\(V_{N}\)があります。ここで、出力電圧を\(V_{OUT}\)としたとき、\(N\)個の入力電圧\(V_{1}\)～\(V_{N}\)と出力電圧\(V_{OUT}\)の関係式は以下のようになります。

この記事では上式の導出方法について説明します。

なお、加算回路の式を見ると以下のことが分かります。

なお、この加算回路は反転増幅回路と回路が似ています。以下の反転増幅回路と加算回路を示します。

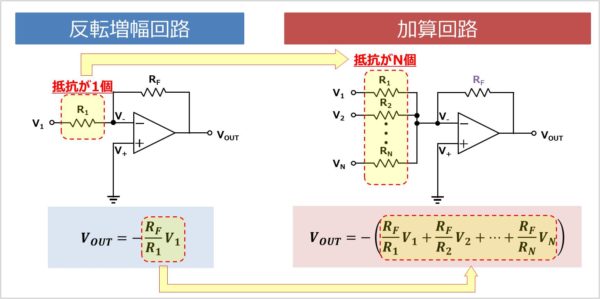
上図より、反転増幅回路の入力電圧と抵抗が\(N\)個になったものが加算回路です。そのため、反転増幅回路を先に勉強すると、加算回路が理解しやすくなります。反転増幅回路については以下の記事で詳しく説明しています。

加算回路の式の導出方法

加算回路の式の導出は以下の順序で行うと簡単に求めることができます。この求め方はその他のオペアンプ回路(反転増幅回路など)にも応用することができます。

順序1：入力端子の電圧\(V_{-}\)と\(V_{+}\)が等しい

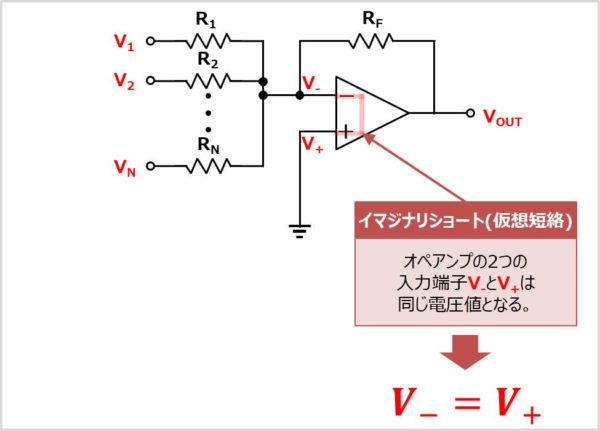
オペアンプの入力端子はイマジナリショート(仮想短絡)のため、反転入力端子\(V_{-}\)と非反転増幅端子\(V_{+}\)の電圧は等しくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{-}=V_{+}\tag{1}
\end{eqnarray}

順序2：反転入力端子\(V_{-}\)の電圧を求める

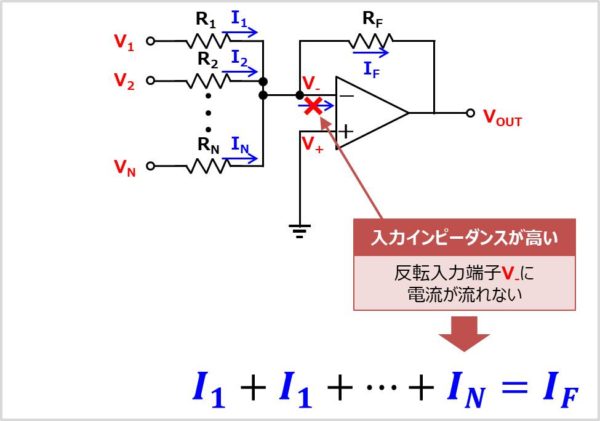
次に反転入力端子\(V_{-}\)の電圧を求めます。オペアンプは入力インピーダンスが高いという特徴があります。そのため、反転入力端子\(V_{-}\)に電流が流れません。

したがって、電流\(I_{1}\)から電流\(I_{N}\)を足したものが電流\(I_{F}\)となります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}+I_{2}+…+I_{N}&=& I_{F}\\
{\Leftrightarrow}\frac{V_{1}-V_{-}}{R_1}+\frac{V_{2}-V_{-}}{R_2}+…+\frac{V_{N}-V_{-}}{R_N}&=&\frac{V_{-}- V_{OUT}}{R_F}\tag{2}
\end{eqnarray}

上式を解くと反転入力端子\(V_{-}\)の電圧を求めることができますが、少し式が複雑になるため、ここはいったん保留して「順序3」に進みます。

順序3：非反転増幅端子\(V_{+}\)の電圧を求める

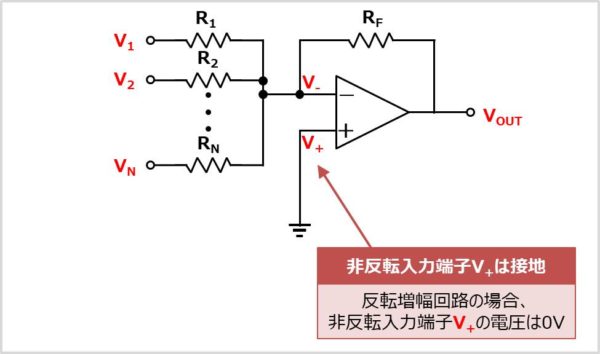
加算回路の場合、非反転増幅端子\(V_{+}\)は接地されているため、0Vとなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{+}=0\tag{3}
\end{eqnarray}

順序4：「順序1」～「順序3」を合体する

「順序1」～「順序3」で求めた式を用いて加算回路の式を求めます。

(1)式と(3)式より、反転入力端子\(V_{-}\)の電圧は
\begin{eqnarray}
V_{-}=0\tag{4}
\end{eqnarray}
となります。ここで(4)式を(2)式に代入すると、加算回路の式を求めることができます。
\begin{eqnarray}
&&\frac{V_{1}}{R_1}+\frac{V_{2}}{R_2}+…+\frac{V_{N}}{R_N}=\frac{-V_{OUT}}{R_F}\\
{\Leftrightarrow}&&V_{OUT}=-\left(\frac{R_F}{R_1}V_{1}+\frac{R_F}{R_2}V_{2}+…+\frac{R_F}{R_N}V_{N}\right)
\end{eqnarray}