この記事では微分回路の式の導出方法を図を用いて分かりやすく説明します。
また、微分回路は反転増幅回路の抵抗の1つがコンデンサに置き換わった回路なので、反転増幅回路の式を利用すれば、簡単に微分回路の式を導出することもできます。この簡単な導出方法はこの記事の後半に説明します。
微分回路の式
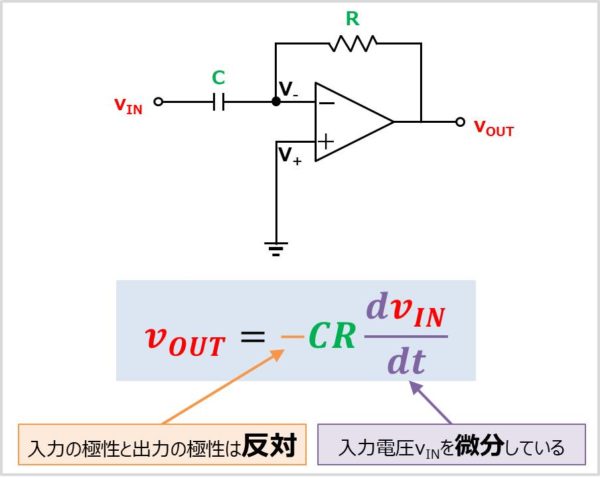
上図に微分回路(Differentiation Circuit)の式を示します。微分回路の入力電圧を\(v_{IN}\)、出力電圧を\(v_{OUT}\)としたとき、入力電圧\(v_{IN}\)と出力電圧\(v_{OUT}\)の関係式は以下のようになります。
v_{OUT}=-CR\frac{dv_{IN}}{dt}
\end{eqnarray}
この記事では上式の導出方法について説明します。
なお、微分回路の式を見ると以下のことが分かります。
- 入力電圧\(v_{IN}\)を微分しています。そのため、微分回路と呼ばれています。
- 反転増幅回路における抵抗の1つがコンデンサに置き換わった回路のため、入力と出力の極性は反対になります。
なお、この微分回路は反転増幅回路と回路が似ています。以下の反転増幅回路と微分回路を示します。
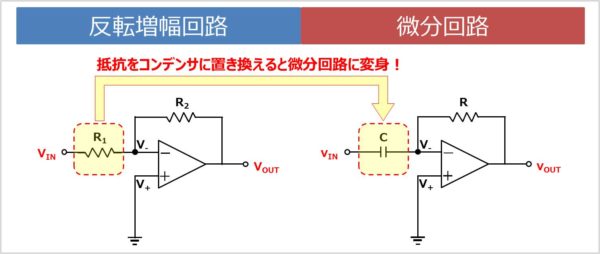
上図より、反転増幅回路の抵抗の1つがコンデンサに置き換わったものが微分回路ということが分かります。そのため、反転増幅回路を先に勉強すると、微分回路が理解しやすくなります。反転増幅回路については以下の記事で詳しく説明しています。 続きを見る

『反転増幅回路』を分かりやすく解説!【オペアンプ】
なお、微分回路はコンデンサ\(C\)と抵抗\(R\)の位置を変えると、積分回路になります。以下に積分回路を示します。
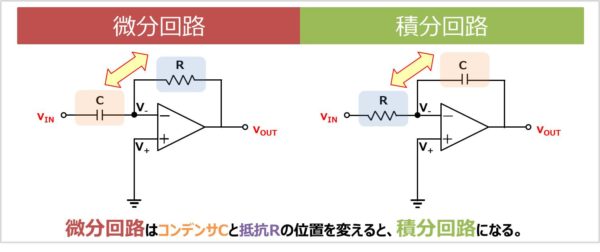

微分回路の式の導出方法
微分回路の式の導出は以下の順序で行うと簡単に求めることができます。この求め方はその他のオペアンプ回路(反転増幅回路など)にも応用することができます。
導出の順序
- 順序1:入力端子の電圧\(V_{-}\)と\(V_{+}\)が等しい
- 順序2:反転入力端子\(V_{-}\)の電圧を求める
- 順序3:非反転増幅端子\(V_{+}\)の電圧を求める
- 順序4:「順序1」~「順序3」を合体する
順序1:入力端子の電圧\(V_{-}\)と\(V_{+}\)が等しい
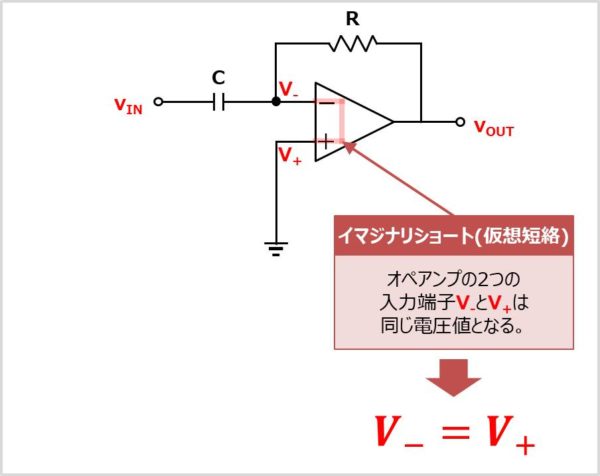

オペアンプの入力端子はイマジナリショート(仮想短絡)のため、反転入力端子\(V_{-}\)と非反転増幅端子\(V_{+}\)の電圧は等しくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{-}=V_{+}\tag{1}
\end{eqnarray}
【補足】イマジナリショート(仮想短絡)とは?
順序2:反転入力端子\(V_{-}\)の電圧を求める
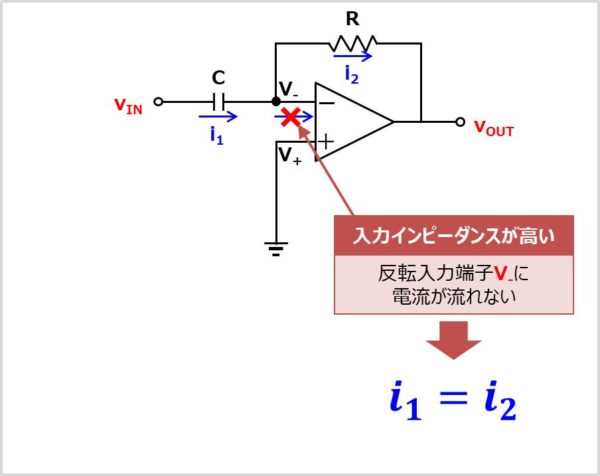

次に反転入力端子\(V_{-}\)の電圧を求めます。オペアンプは入力インピーダンスが高いという特徴があります。そのため、反転入力端子\(V_{-}\)に電流が流れません。
したがって、コンデンサ\(C\)に流れる電流\(i_{1}\)と抵抗\(R\)に流れる電流\(i_{2}\)が等しくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
i_{1}&=&i_{2}\\
{\Leftrightarrow}C\frac{d(v_{IN}-V_{-})}{dt}&=&\frac{V_{-}- v_{OUT}}{R}\tag{2}
\end{eqnarray}
上式を解くと反転入力端子\(V_{-}\)の電圧を求めることができますが、少し式が複雑になるため、ここはいったん保留して「順序3」に進みます。
【補足】コンデンサの基本式


順序3:非反転増幅端子\(V_{+}\)の電圧を求める
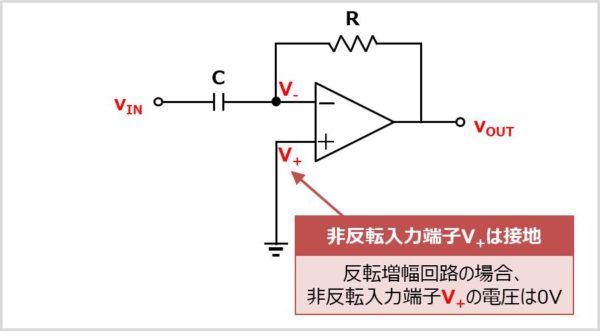

微分回路の場合、非反転増幅端子\(V_{+}\)は接地されているため、0Vとなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{+}=0\tag{3}
\end{eqnarray}
順序4:「順序1」~「順序3」を合体する
「順序1」~「順序3」で求めた式を用いて、微分回路の式を求めます。
(1)式と(3)式より、反転入力端子\(V_{-}\)の電圧は
\begin{eqnarray}
V_{-}=0\tag{4}
\end{eqnarray}
となります。ここで(4)式を(2)式に代入すると、微分回路の式を求めることができます。
\begin{eqnarray}
&&C\frac{dv_{IN}}{dt}=\frac{-v_{OUT}}{R}\\
{\Leftrightarrow}&&v_{OUT}=-CR\frac{dv_{IN}}{dt}\tag{5}
\end{eqnarray}
これが微分回路の式の基本的な導出方法です。次に反転増幅回路を用いた簡単な導出方法について説明します。
微分回路の式(簡単な導出方法)
下図の反転増幅回路の式は以下のようになっており、増幅度は抵抗\(R_1\)と抵抗\(R_2\)によって決まります。また、微分回路は反転増幅回路において、入力電圧\(v_{IN}\)と接続されている抵抗\(R_1\)がコンデンサ\(C\)に入れ替わった回路となっています。
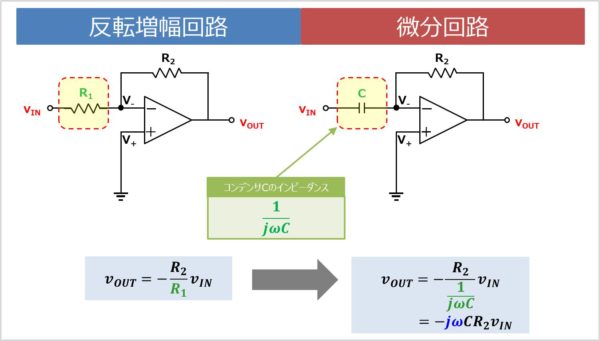

ここで、コンデンサ\(C\)のインピーダンスは\(\displaystyle\frac{1}{j{\omega}C}\)なので、\(R_1\)を\(\displaystyle\frac{1}{j{\omega}C}\)に置き換えます。すると入力電圧\(v_{IN}\)と出力電圧\(v_{OUT}\)の関係は以下の式となります。
\begin{eqnarray}
v_{OUT}&=&-\displaystyle\frac{R_2}{\displaystyle\frac{1}{j{\omega}C}}v_{IN}\\
&=&-j{\omega}CR_2v_{IN}\tag{6}
\end{eqnarray}
ここで、話が少し変わりますが、交流電圧の微分と積分について説明します。
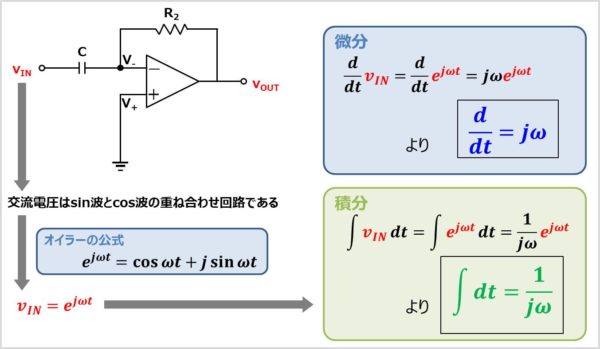

交流電圧はsin波とcos波の重ね合わせなので、回路の入力電圧\(v_{IN}\)は\({\sin}\)と\({\cos}\)の和で表すことができます。また、有名なオイラーの公式は以下の式となっており、\(e^{j{\omega}t}\)も\({\sin}\)と\({\cos}\)の和となっています。
\begin{eqnarray}
e^{j{\omega}t}={\cos}{\omega}t+j{\sin}{\omega}t\tag{7}
\end{eqnarray}
そのため、オイラーの公式を用いると、入力電圧\(v_{IN}\)は\(e^{j{\omega}t}\)で表すことができます。以下に式を示します。
\begin{eqnarray}
v_{IN}=e^{j{\omega}t}\tag{8}
\end{eqnarray}
この入力電圧\(v_{IN}=e^{j{\omega}t}\)を微分すると、以下の式が成り立ちます。
\begin{eqnarray}
&&\frac{d}{dt}v_{IN}=\frac{d}{dt}e^{j{\omega}t}=j{\omega}e^{j{\omega}t}\\
{\Leftrightarrow}&&\displaystyle\frac{d}{dt}=j{\omega}\tag{9}
\end{eqnarray}
(9)式を(6)式に代入すると、入力電圧\(v_{IN}\)と出力電圧\(v_{OUT}\)の関係式は以下のようになります。
\begin{eqnarray}
v_{OUT}&=&-j{\omega}CR_2v_{IN}\\
&=&-CR_2\frac{dv_{IN}}{dt}
\end{eqnarray}
基本的な求め方と同じ式になりましたね。上記の導出方法のように、反転増幅回路の式、コンデンサ\(C\)のインピーダンス\(\displaystyle\frac{1}{j{\omega}C}\)、そして\(\displaystyle\frac{d}{dt}=j{\omega}\)の式が分かっていれば、簡単に微分回路の式を導出することができます。






