【交流回路とベクトル】インピーダンスなどにつく「・(ドット)」の意味！

この記事では、

インピーダンスZ・電圧V・電流Iなどにつく「・(ドット)」の意味
『交流回路の式』を『ベクトル』に変換する方法
『ベクトル』を『交流回路の式』に変換する方法

などを図を用いて分かりやすく説明するよう心掛けています。ご参考になれば幸いです。

インピーダンス・電圧・電流などにつく「・(ドット)」の意味

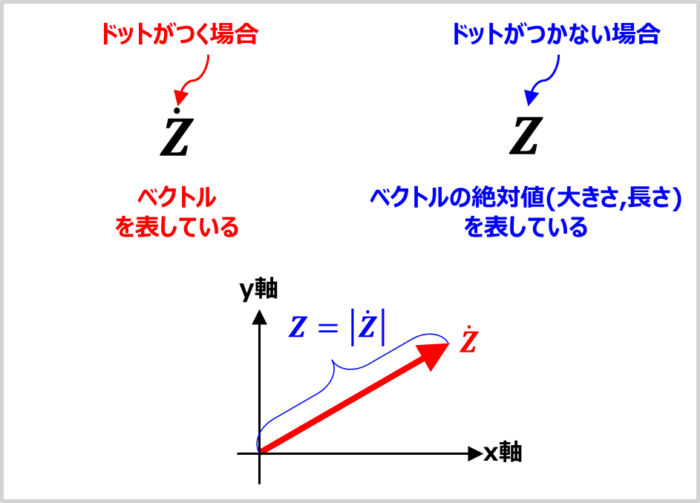
『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』などの記号の上に「・(ドット)」がつき、\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\)と記載されている場合があります。

このドットが付いた\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\)などは「ベクトルですよ！」ということを表しています。

『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』などの記号の上に「・(ドット)」がつく場合とつかない場合では下記に示すように意味が異なります。

記号の上にドットがつく場合(\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\)など)

ベクトルを表している。

記号の上にドットがつかない場合(\(Z\)・\(V\)・\(I\)など)

ベクトルの絶対値(大きさ,長さ)を表している。

直流回路の場合、インピーダンス等の記号の上にドットを付けてベクトル表記(\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\))にする必要がありません。

例えば、電圧\(V=10{\mathrm{[V]}}\)の電池に\(R=5{\mathrm{[{\Omega}]}}\)の抵抗を接続すると、オームの法則より流れる電流\(I\)を次式のように計算することができるからです。

\begin{eqnarray}
I=\frac{V}{R}=\frac{10}{5}=2{\mathrm{[A]}}
\end{eqnarray}

しかし交流回路の場合、直流回路には無かった「位相」という新たなパラメータが出てきます。この位相は交流の時間的なズレ(電流や電圧の遅れや進み)を表しています。

『インピーダンス\(Z\)』や『電圧\(V\)』や『電流\(I\)』をベクトル表記(\({\dot{Z}}\)・\({\dot{V}}\)・\({\dot{I}}\))にすることで、「大きさ」と「位相」の両方を表すことができます。なお、ベクトルの向きの角度が「位相」を表します。

交流回路は周波数を一定とした場合、「大きさ」と「位相」を考えればよいので、ベクトルが役に立つのです。

では、次に交流回路のベクトルについて

『交流回路の式』を『ベクトル』に変換する方法
『ベクトル』を『交流回路の式』に変換する方法

などを具体例を用いて説明していきます。

交流回路のベクトルによる表し方

最初に交流回路のベクトルによる表し方に関して基本的なルールを説明します。

交流回路のベクトルによる表し方

ベクトルの絶対値は『ベクトルの長さ(大きさ)』と『交流の実効値』を表している。
基準からの角度\({\theta}{\mathrm{[rad]}}\)は位相を表している。
ベクトルが基準から反時計周りに回転している場合、位相が進んでおり、位相は『正(プラス)』となる。
ベクトルが基準から時計周りに回転している場合、位相は遅れており、位相は『負(マイナス)』となる。

では上記のルールを用いて『交流回路の式』を『ベクトル』に変換してみましょう。

基準について

ベクトルの基準は自由に決めることはできますが、一般的にはxy座標のx軸を基準とします。この記事でもx軸を基準として考えています。

『交流回路の式』を『ベクトル』に変換する方法

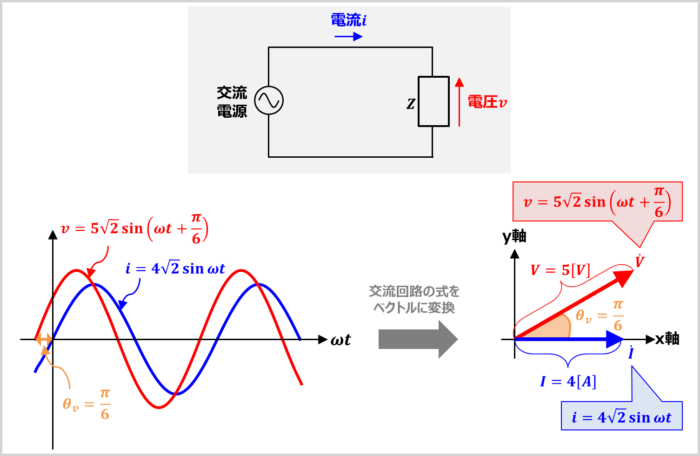
上図に示すように、インピーダンス\(Z\)に交流電源を接続した時、『インピーダンス\(Z\)にかかる電圧\(v\)』と『インピーダンス\(Z\)に流れる電流\(i\)』が下記の式であるとします。

\begin{eqnarray}
v&=&V_M{\sin}\left({\omega}t+{\theta}_v\right)=5\sqrt{2}{\sin}\left({\omega}t+\frac{{\pi}}{6}\right){\mathrm{[V]}}\\
\\
i&=&I_M{\sin}\left({\omega}t+{\theta}_i\right)=4\sqrt{2}{\sin}{\omega}t{\mathrm{[A]}}\\
\end{eqnarray}

上式の『交流回路の式』を『ベクトル』に変換してみましょう。

インピーダンス\(Z\)にかかる電圧\({\dot{V}}\)のベクトル

インピーダンス\(Z\)にかかる電圧\(v\)の実効値\(V_{RMS}\)は以下の値になります。

\begin{eqnarray}
V_{RMS}=\frac{V_M}{\sqrt{2}}=\frac{5\sqrt{2}}{\sqrt{2}}=5{\mathrm{[V]}}
\end{eqnarray}

『ベクトル\({\dot{V}}\)の長さ(大きさ)\(V\)』は『ベクトル\({\dot{V}}\)の絶対値\(|{\dot{V}}|\)』であり、その値は『電圧\(v\)の実効値\(V_{RMS}\)』になるため以下の式が成り立ちます。

\begin{eqnarray}
V=|{\dot{V}}|=V_{RMS}=5{\mathrm{[V]}}
\end{eqnarray}

また、インピーダンス\(Z\)にかかる電圧\(v\)の位相\({\theta}_v\)は以下の値になります。

\begin{eqnarray}
{\theta}_v=+\frac{{\pi}}{6}{\mathrm{[rad]}}
\end{eqnarray}

したがって、上図に示すようにインピーダンス\(Z\)にかかる電圧\({\dot{V}}\)のベクトルは基準(x軸)から反時計周りに\(\displaystyle\frac{{\pi}}{6}{\mathrm{[rad]}}\)回転させた向きとなります。

インピーダンス\(Z\)に流れる電流\({\dot{I}}\)のベクトル

インピーダンス\(Z\)に流れる電流\(i\)の実効値\(I_{RMS}\)は以下の値になります。

\begin{eqnarray}
I_{RMS}=\frac{I_M}{\sqrt{2}}=\frac{4\sqrt{2}}{\sqrt{2}}=4{\mathrm{[A]}}
\end{eqnarray}

『ベクトル\({\dot{I}}\)の長さ(大きさ)\(I\)』は『ベクトル\({\dot{I}}\)の絶対値\(|{\dot{I}}|\)』であり、その値は『電流\(i\)の実効値\(I_{RMS}\)』になるため以下の式が成り立ちます。

\begin{eqnarray}
I=|{\dot{I}}|=I_{RMS}=4{\mathrm{[A]}}
\end{eqnarray}

また、インピーダンス\(Z\)にかかる流れる電流\(i\)の位相\({\theta}_i\)は以下の値になります。

\begin{eqnarray}
{\theta}_i=0{\mathrm{[rad]}}
\end{eqnarray}

したがって、上図に示すようにインピーダンス\(Z\)に流れる電流\({\dot{I}}\)のベクトルは基準(x軸)と同じ向きになります。

インピーダンス\(Z\)にかかる電圧\({\dot{V}}\)はインピーダンス\(Z\)に流れる電流\({\dot{I}}\)を基準とすると、反時計周りに\(\displaystyle\frac{{\pi}}{6}{\mathrm{[rad]}}\)回転した向きとなります。

そのため、インピーダンス\(Z\)にかかる電圧\({\dot{V}}\)はインピーダンス\(Z\)に流れる電流\({\dot{I}}\)よりも位相が\(\displaystyle\frac{{\pi}}{6}{\mathrm{[rad]}}\)進んでいるということになります。

『ベクトル』を『交流回路の式』に変換する方法

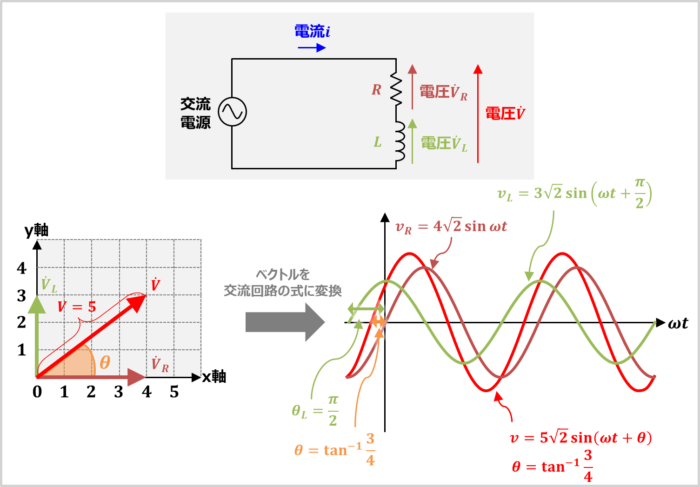
抵抗\(R\)とコイル\(L\)で構成されたRL直列回路に交流電圧を接続した時、抵抗\(R\)にかかる電圧\({\dot{V}_R}\)、コイル\(L\)にかかる電圧\({\dot{V}}_L\)、RL直列回路にかかる電圧\({\dot{V}}\)の関係が上図に示すようなベクトルであるとします。

これらの『ベクトル』を『交流回路の式』に変換してみましょう。

抵抗\(R\)にかかる電圧\(v_R\)

『抵抗\(R\)にかかる電圧\(v_R\)の実効値\(V_{RRMS}\)』は『ベクトル\({\dot{V}_R}\)の長さ(大きさ)\(V_R\)』になります。そのため、『抵抗\(R\)にかかる電圧\(v_R\)の実効値\(V_{RRMS}\)』は以下の値となります。

\begin{eqnarray}
V_{RRMS}=V_R=4{\mathrm{[V]}}
\end{eqnarray}

したがって、『抵抗\(R\)にかかる電圧\(v_R\)の最大値\(V_{RM}\)』は以下の値になります。

\begin{eqnarray}
V_{RM}=\sqrt{2}×V_{RRMS}=4\sqrt{2}{\mathrm{[V]}}
\end{eqnarray}

また、抵抗\(R\)にかかる電圧\({\dot{V}_R}\)のベクトルは基準(x軸)と同じ向きであるため、位相\({\theta}_R\)は以下の値となります。

\begin{eqnarray}
{\theta}_R=0{\mathrm{[rad]}}
\end{eqnarray}

以上より、『抵抗\(R\)にかかる電圧\(v_R\)』は次式で表されます。

\begin{eqnarray}
v_R&=&V_{RM}{\sin}\left({\omega}t+{\theta}_R\right)=4\sqrt{2}{\sin}{\omega}t{\mathrm{[V]}}
\end{eqnarray}

コイル\(L\)にかかる電圧\(v_L\)

『コイル\(L\)にかかる電圧\(v_L\)の実効値\(V_{LRMS}\)』は『ベクトル\({\dot{V}_L}\)の長さ(大きさ)\(V_L\)』になります。そのため、『コイル\(L\)にかかる電圧\(v_L\)の実効値\(V_{LRMS}\)』は以下の値となります。

\begin{eqnarray}
V_{LRMS}=V_L=3{\mathrm{[V]}}
\end{eqnarray}

したがって、『コイル\(L\)にかかる電圧\(v_L\)の最大値\(V_{LM}\)』は以下の値になります。

\begin{eqnarray}
V_{LM}=\sqrt{2}×V_{LRMS}=3\sqrt{2}{\mathrm{[V]}}
\end{eqnarray}

また、コイル\(L\)にかかる電圧\({\dot{V}_L}\)のベクトルは基準(x軸)から反時計周りに\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)回転させた向きとなります。そのため、位相\({\theta}_L\)は以下の値となります。

\begin{eqnarray}
{\theta}_L=\frac{{\pi}}{2}{\mathrm{[rad]}}
\end{eqnarray}

以上より、『コイル\(L\)にかかる電圧\(v_L\)』は次式で表されます。

\begin{eqnarray}
v_L&=&V_{LM}{\sin}\left({\omega}t+{\theta}_L\right)=3\sqrt{2}{\sin}\left({\omega}t+\displaystyle\frac{{\pi}}{2}\right){\mathrm{[V]}}
\end{eqnarray}

RL直列回路にかかる電圧\(v\)

『ベクトル\({\dot{V}}\)の長さ(大きさ)\(V\)』は三平方の定理(ピタゴラスの定理)より下記の値となります。

\begin{eqnarray}
V=\sqrt{{V_R}^2+{V_L}^2}=\sqrt{{4}^2+{3}^2}=5{\mathrm{[V]}}
\end{eqnarray}

『RL直列回路にかかる電圧\(v\)の実効値\(V_{RMS}\)』は『ベクトル\({\dot{V}}\)の長さ(大きさ)\(V\)』になります。そのため、『RL直列回路にかかる電圧\(v\)の実効値\(V_{RMS}\)』は以下の値となります。

\begin{eqnarray}
V_{RMS}=V=5{\mathrm{[V]}}
\end{eqnarray}

したがって、『RL直列回路にかかる電圧\(v\)の最大値\(V_{M}\)』は以下の値になります。

\begin{eqnarray}
V_M=\sqrt{2}×V_{RMS}=5\sqrt{2}{\mathrm{[V]}}
\end{eqnarray}

また、RL直列回路にかかる電圧\({\dot{V}}\)のベクトルは基準(x軸)から反時計周りに\({\theta}{\mathrm{[rad]}}\)回転させた向きとなります。位相\({\theta}\)は次式で求めることができます。

\begin{eqnarray}
{\tan}{\theta}&=&\displaystyle\frac{V_L}{V_R}\\
\\
&=&\displaystyle\frac{3}{4}\\
\\
{\Leftrightarrow}{\theta}&=&{\tan}^{-1}\displaystyle\frac{3}{4}{\mathrm{[rad]}}\\
\\
&{\approx}&36.87^{\circ}
\end{eqnarray}

以上より、『RL直列回路にかかる電圧\(v\)』は次式で表されます。

\begin{eqnarray}
v&=&V_{M}{\sin}\left({\omega}t+{\theta}\right)=5\sqrt{2}{\sin}\left({\omega}t+{\theta}\right){\mathrm{[V]}}\\
\\
ただし{\theta}&=&{\tan}^{-1}\displaystyle\frac{3}{4}{\mathrm{[rad]}}
\end{eqnarray}