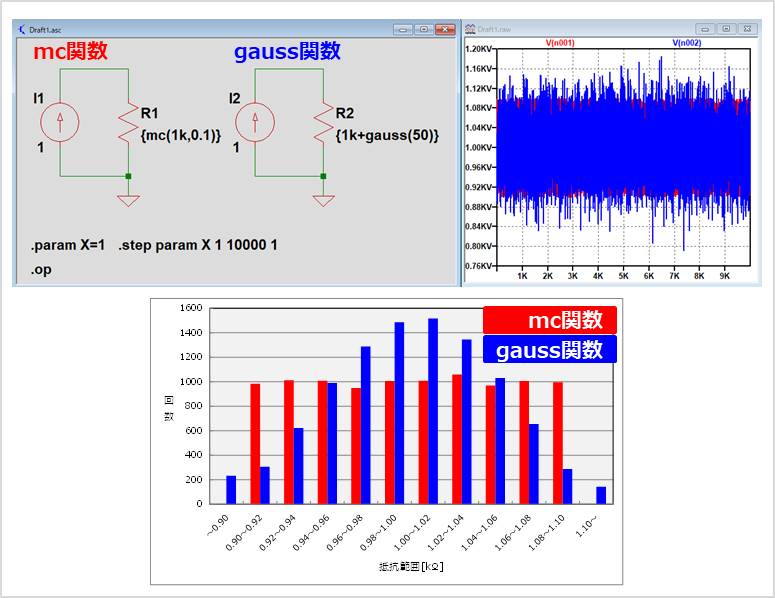
この記事では、モンテカルロ解析の方法と、モンテカルロ解析に用いるmc関数とgauss関数の使い方について説明します。
モンテカルロ解析とは
回路設計において、回路を構成している抵抗やコンデンサ等の部品交差(バラツキ)を考慮したい時があります。モンテカルロ解析とは、部品の素子値がばらついた場合において、回路の挙動がどのように変化するかをシミュレーションすることができる解析です。
LTspiceにはこのモンテカルロ解析を行うためのmc関数があります。
例えば、抵抗値が1kΩで公差が10%である抵抗の抵抗値は0.9kΩから1.1kΩのバラツキがあります。mc関数を用いるとシミュレーション毎に0.9kΩから1.1kΩの間でランダムに変化する抵抗を作ることができます。
モンテカルロ解析は回路の歩留まりの検証などを行うことができるため、試作・量産化を想定したシミュレーションでは必要不可欠な解析となります。
モンテカルロ解析に用いる『mc関数』の構文
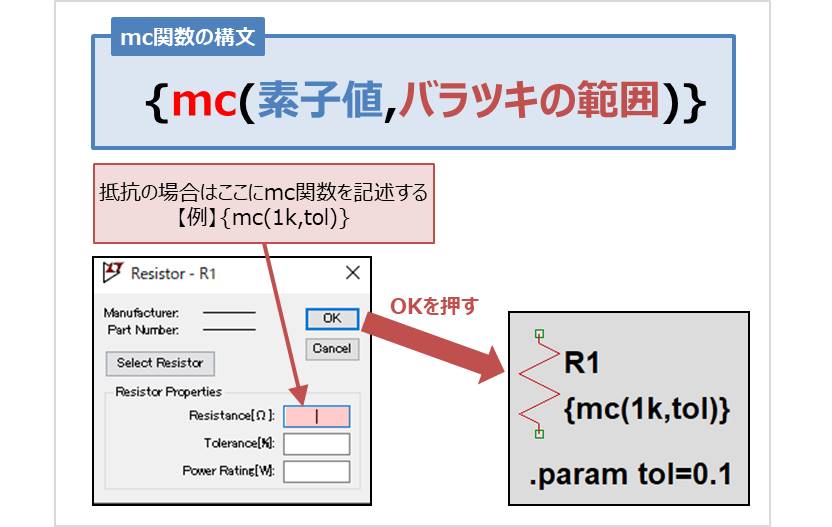
mc関数の構文は
となります。
例えば、抵抗1kΩ(公差10%)の抵抗をmc関数で作成する際には、抵抗を右クリックした際に出てくる画面内のResistance[Ω]の箇所に
と入力します。ここで、バラツキの範囲に変数tolを用いています。変数tolを「.param」を用いて定義します。バラツキの範囲(公差)が10%の場合には以下のように記述します。
なお、変数tolを用いずに直接、
と記述しても大丈夫です。なお、変数tolはtolerance(公差という意味)の頭文字3文字から取っています。
モンテカルロ解析のシミュレーション例
.tran解析でモンテカルロ解析を使用
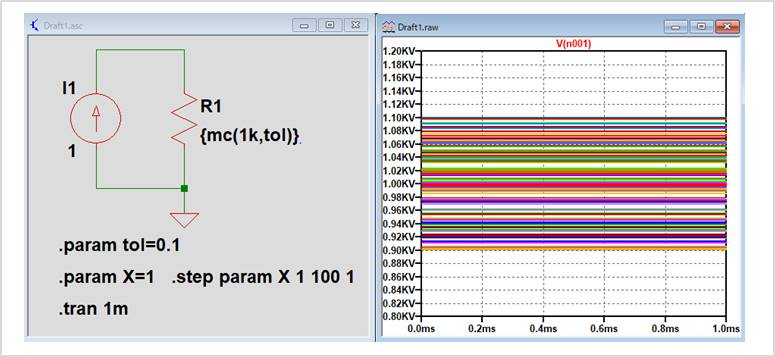
1kΩ(公差10%)の抵抗R1に対して1Aの電流を流した時の出力電圧を観測します。このようにする事で、抵抗R1にかかる電圧値と抵抗R1の抵抗値が等しくなります。
1kΩ(公差10%)の抵抗R1は、
と記述します(.param tol=0.1と定義した場合)。
1回のシミュレーションでmc関数から得られる抵抗値は1つとなります。そのため、「.stepコマンド」を用いて複数回シミュレーションを実行する必要があります。今回は、ダミーの変数Xを「.param X=1」と定義し、
と記述することで、シミュレーションを0〜99の100回繰り返し行っています。なお、「.stepコマンド」について詳しくは以下の記事に記載しているので参考にしてください。
【LTspice】.stepコマンドとは
シミュレーション時間は「.tran 1m」と記述することで、1[ms]としています。
シミュレーション結果を見ると、抵抗R1にかかる電圧(すなわち抵抗値)が0.9kΩから1.1kΩの間でばらついていることが確認できます。
.op解析でモンテカルロ解析を使用
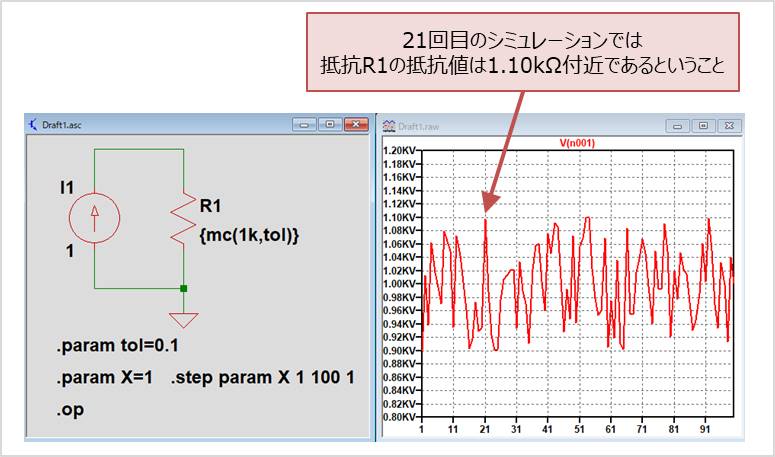
次に「.op解析」を行ってみます。先ほどの「.tran解析」でのシミュレーションで記述した「.tran 1m」を「.op」に置き換えることで「.op解析」を実行することができます。「.op解析」について詳しくは以下の記事に記載しているので参考にしてください。
【LTspice】OP解析とは?回路図に電圧を表示する方法!
シミュレーション結果のグラフにおいて、横軸はシミュレーション実行回数となります。縦軸は各シミュレーションにおける抵抗にかかる電圧(すなわち抵抗値)となります。例えば、横軸で21の箇所を見ると約1.10kΩ(1.10kV)となっています。これは、21回目のシミュレーションでは、抵抗R1の抵抗値は1.10kΩ付近であるということを指します。
上記のシミュレーションにおいても抵抗値が0.9kΩ〜1.1kΩでばらついていることが分かりますが、どのような分布でバラついているかは分かりません。そこで、このグラフデータをExcelに取り込みヒストグラフで表示してみます。以下にヒストグラフを示します。{mc(1k,tol)}で記述した抵抗R1の抵抗値のバラツキは一様の分布になっていることが分かります。
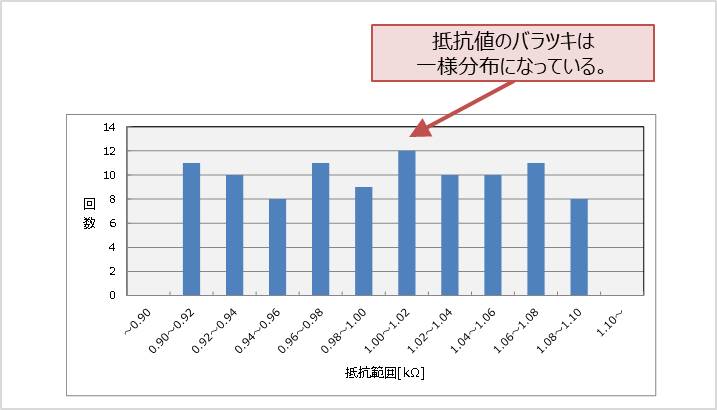
なお、グラフデータをExcelで表示する方法については以下の記事を参考にしてください。
【LTspice】波形プロットをテキスト出力して、Excelにインポートする方法
mc解析とgauss関数の違い
mc関数ではなく、gauss関数を用いても回路部品のバラツキを検証することができます。mc関数とgauss関数の違いは以下となっています。
x*(1-y)~x*(1+y)で一様分布の乱数を発生させる。
例えば、{mc(1k,0.1)}ではバラツキが±10%となり、0.9k~1.1kの範囲で一様分布の乱数を発生させる。
標準偏差xの正規分布の乱数を発生させる。
例えば、{1k+gauss(50)}では、平均値を1kとして、標準偏差50の正規分布の乱数を発生させる。
以下にmc関数とgauss関数を用いた時のシミュレーションを10000回実行した時の結果とそのヒストグラムを示しています。mc関数が一様分布の乱数で、gauss関数が正規分布の乱数を発生してることが確認できます。