ラプラス変換の「定義式」と「公式の導出方法」

この記事では『ラプラス変換』について

ラプラス変換の定義式
ラプラス変換の定義式を用いて公式を導出する方法

などを分かりやすく説明するように心掛けています。ご参考になれば幸いです。

ラプラス変換の定義式

時間\(t\)の関数\(f(t)\)のラプラス変換\(F(s)\)は次式で定義されます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]={\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\tag{1}
\end{eqnarray}

(1)式は時間\(t\)の関数\(f(t)\)に\(e^{-st}\)を掛けたものを\(t=0\)から\({\infty}\)まで積分すると、\(s\)の関数\(F(s)\)に変換できるということを示しています。

また、上式の記号\(\displaystyle\mathcal{L}\)はラプラス変換を表す記号です。\(\displaystyle\mathcal{L}\left[f(t)\right]\)と書くと、時間\(t\)の関数\(f(t)\)をラプラス変換するということになります。なお、\(\displaystyle\mathcal{L}\)はラプラス(Laplace)の頭文字を筆記体で書いたものです。

では実際に、ラプラス変換の定義式を用いて公式を導出してみましょう。

補足

ラプラス変換した後の関数は、一般的には大文字の\(F(s)\)を用います。
\(s\)はラプラス演算子といいます。
ラプラス変換は英語では「Laplace transform」と書きます。

ラプラス変換の定義式を用いて公式を導出してみよう

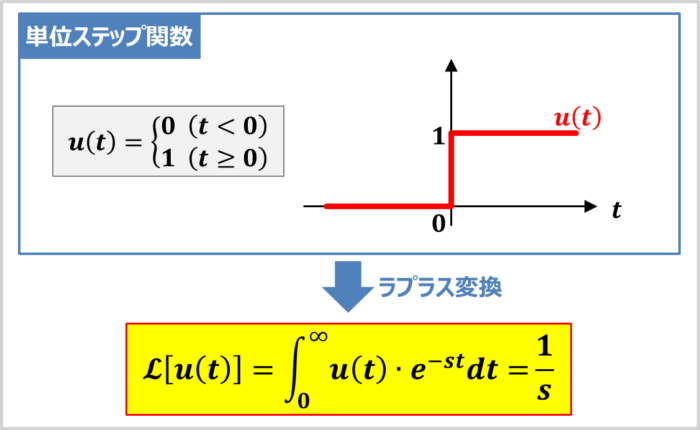
単位ステップ関数\(f(t)=u(t)\)は次式で表されます。

\begin{eqnarray}
u(t)=
\begin{cases}
0&(t{<}0)\\
1&(t{≥}0)
\end{cases}
\tag{2}
\end{eqnarray}

単位ステップ関数\(u(t)\)のラプラス変換の公式を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[u(t)\right]=\displaystyle\frac{1}{s}\tag{3}
\end{eqnarray}

(3)式から分かるように、単位ステップ関数\(u(t)\)をラプラス変換すると、「\(\displaystyle\frac{1}{s}\)」になります。

では実際に、(1)式の定義式を用いて、公式を導出してみましょう。単位ステップ関数\(u(t)\)をラプラス変換をラプラス変換すると次式となります。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[u(t)\right]&=&{\displaystyle\int}_0^{\infty}u(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}1{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&-\displaystyle\frac{1}{s}\left[e^{-st}\right]_0^{\infty}\\
\\
&=&-\displaystyle\frac{1}{s}\left(e^{-s{\;}{\cdot}{\;}{\infty}}-e^{-s{\;}{\cdot}{\;}0}\right)\\
\\
&=&-\displaystyle\frac{1}{s}\left(0-1\right)\\
\\
&=&\displaystyle\frac{1}{s}\tag{4}
\end{eqnarray}

通常、ラプラス変換の公式「\(F(s)=\displaystyle\mathcal{L}\left[u(t)\right]=\displaystyle\frac{1}{s}\)」は覚えますが、公式を忘れてしまった場合には、(1)式の定義式を用いれば導出することができるので、(1)式は覚えましょう！