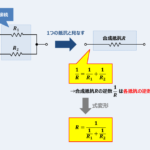
この記事では『分流の法則』について
- 分流の法則とは
- 分流の法則の『公式』・『公式の導出方法』・『例題』
- 「分流の法則」と「分圧の公式」の違い
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
分流の法則とは
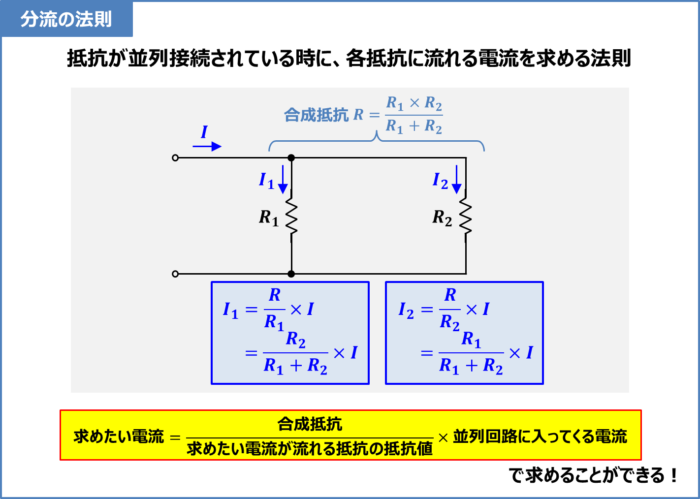
分流の法則は、抵抗が並列接続されている時に、各抵抗に流れる電流を求める法則です。
上図に抵抗\(R_1{\mathrm{[{\Omega}]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)を並列接続し、電源電圧\(V{\mathrm{[V]}}\)を印加した回路を示しています。
この回路において、並列回路に入ってくる電流を\(I{\mathrm{[A]}}\)、合成抵抗を\(R{\mathrm{[{\Omega}]}}\)とすると、抵抗\(R_1{\mathrm{[{\Omega}]}}\)に流れる電流\(I_1{\mathrm{[A]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)に流れる電流\(I_2{\mathrm{[A]}}\)は次式で表されます。
\begin{eqnarray}
I_1&=&\frac{R}{R_1}×I=\frac{R_2}{R_1+R_2}×I{\mathrm{[A]}}\tag{1}\\
\\
I_2&=&\frac{R}{R_2}×I=\frac{R_1}{R_1+R_2}×I{\mathrm{[A]}}\tag{2}
\end{eqnarray}
(1)式と(2)式が分流の公式となります。
抵抗\(R_1\)と\(R_2\)によって、電流\(I\)が\(I_1\)と\(I_2\)に分けられています。つまり、分流されているということになります。
分流の公式は次式で導出することができます。
\begin{eqnarray}
\mbox{求めたい電流}=\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\tag{3}
\end{eqnarray}
では実際に(3)式から(1)式と(2)式を導出してみましょう。
抵抗\(R_1{\mathrm{[{\Omega}]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)の合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R=\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}=\frac{R_1×R_2}{R_1+R_2}{\mathrm{[{\Omega}]}}\tag{4}
\end{eqnarray}
あわせて読みたい
並列接続された抵抗の合成抵抗の『求め方』や『例題』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

抵抗の並列接続!合成抵抗の『式』や『証明』などを解説!
続きを見る
(4)式を(3)式に代入すると、抵抗\(R_1{\mathrm{[{\Omega}]}}\)に流れる電流\(I_1{\mathrm{[A]}}\)は次式となり、(1)式を導出することができます。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_1&=&\frac{\displaystyle\frac{R_1×R_2}{R_1+R_2}}{R_1}×I\\
\\
&=&\frac{R_2}{R_1+R_2}×I{\mathrm{[A]}}\tag{5}
\end{eqnarray}
同様に、(4)式を(3)式に代入すると、抵抗\(R_2{\mathrm{[{\Omega}]}}\)に流れる電流\(I_2{\mathrm{[A]}}\)は次式となり、(2)式を導出することができます。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_2&=&\frac{\displaystyle\frac{R_1×R_2}{R_1+R_2}}{R_2}×I\\
\\
&=&\frac{R_1}{R_1+R_2}×I{\mathrm{[A]}}\tag{6}
\end{eqnarray}
このように、抵抗が並列接続されている場合、
\begin{eqnarray}
\mbox{求めたい電流}=\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\tag{7}
\end{eqnarray}
を用いて、各抵抗に流れる電流を求めることをオススメします。この上式を覚えておけば、並列接続されている抵抗が3つ以上でも分流の公式を導出することができますよ。
補足
- 分流の法則は英語では「Current Divider Rule」と書きます。
分流の法則の例題(抵抗が2つ並列接続されている時)
例題
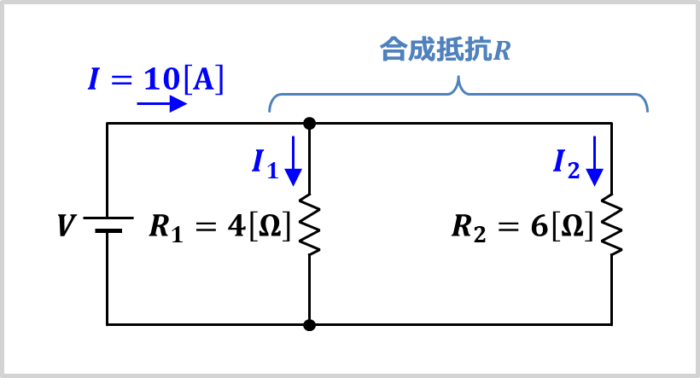

上図に示した回路において、並列回路に入ってくる電流\(I\)が\(10{\mathrm{[A]}}\)、抵抗\(R_1\)が\(4{\mathrm{[{\Omega}]}}\)、抵抗\(R_2\)が\(6{\mathrm{[{\Omega}]}}\)の時、
- 抵抗\(R_1\)と抵抗\(R_2\)の合成抵抗\(R\)は何\({\mathrm{{\Omega}}}\)でしょうか。
- 抵抗\(R_1\)に流れる電流\(I_1\)は何\({\mathrm{A}}\)でしょうか。
- 抵抗\(R_2\)に流れる電流\(I_2\)は何\({\mathrm{A}}\)でしょうか。
解答
抵抗\(R_1\)と抵抗\(R_2\)の合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R=\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}}=\frac{R_1×R_2}{R_1+R_2}=\frac{4×6}{4+6}=2.4{\mathrm{[{\Omega}]}}\tag{8}
\end{eqnarray}
したがって、抵抗\(R_1\)に流れる電流\(I_1{\mathrm{[A]}}\)は以下の値になります。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_1&=&\frac{2.4}{4}×10\\
\\
&=&6{\mathrm{[A]}}\tag{9}
\end{eqnarray}
同様に、抵抗\(R_2\)に流れる電流\(I_2{\mathrm{[A]}}\)は以下の値になります。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_2&=&\frac{2.4}{6}×10\\
\\
&=&4{\mathrm{[A]}}\tag{10}
\end{eqnarray}
【分流の法則】抵抗が3つ並列接続されている時
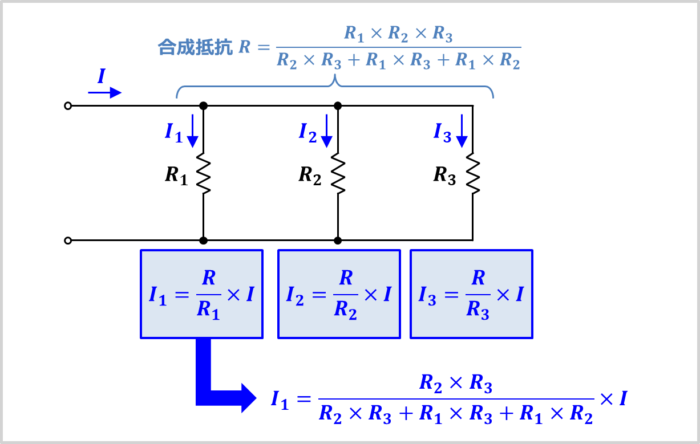

上図に抵抗\(R_1{\mathrm{[{\Omega}]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)と抵抗\(R_3{\mathrm{[{\Omega}]}}\)を並列接続し、電源電圧\(V{\mathrm{[V]}}\)を印加した回路を示しています。
この回路において、並列回路に入ってくる電流を\(I{\mathrm{[A]}}\)とすると、抵抗\(R_1{\mathrm{[{\Omega}]}}\)に流れる電流\(I_1{\mathrm{[A]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)に流れる電流\(I_2{\mathrm{[A]}}\)と抵抗\(R_3{\mathrm{[{\Omega}]}}\)に流れる電流\(I_3{\mathrm{[A]}}\)は次式で表されます。
\begin{eqnarray}
I_1&=&\frac{R}{R_1}×I=\frac{R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}×I{\mathrm{[A]}}\tag{11}\\
\\
I_2&=&\frac{R}{R_2}×I=\frac{R_1×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}×I{\mathrm{[A]}}\tag{12}\\
\\
I_3&=&\frac{R}{R_3}×I=\frac{R_1×R_2}{R_2×R_3+R_1×R_3+R_1×R_2}×I{\mathrm{[A]}}\tag{13}
\end{eqnarray}
上式も同様に
\begin{eqnarray}
\mbox{求めたい電流}=\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\tag{14}
\end{eqnarray}
で導出することができます。では実際に(14)式から(11)式を導出してみましょう。
抵抗\(R_1{\mathrm{[{\Omega}]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)と抵抗\(R_3{\mathrm{[{\Omega}]}}\)の合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R&=&\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
\\
&=&\frac{R_1×R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}\tag{15}
\end{eqnarray}
(15)式を(14)式に代入すると、抵抗\(R_1{\mathrm{[{\Omega}]}}\)に流れる電流\(I_1{\mathrm{[A]}}\)は次式となり、(11)式を導出することができます。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_1&=&\frac{\displaystyle\frac{R_1×R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}}{R_1}×I\\
\\
&=&\frac{R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}×I{\mathrm{[A]}}\tag{16}
\end{eqnarray}
(15)式と(16)式も上記に示したような方法で導出することができます。
分流の法則の例題(抵抗が3つ並列接続されている時)
例題
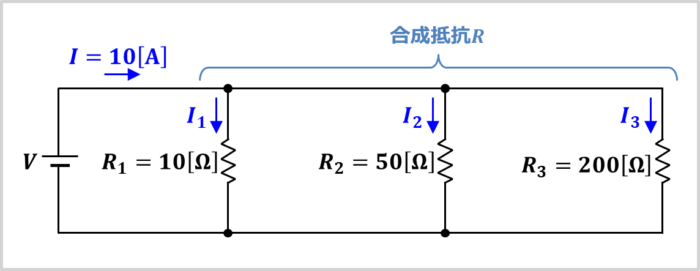

上図に示した回路において、並列回路に入ってくる電流\(I\)が\(10{\mathrm{[A]}}\)、抵抗\(R_1\)が\(10{\mathrm{[{\Omega}]}}\)、抵抗\(R_2\)が\(50{\mathrm{[{\Omega}]}}\)、抵抗\(R_3\)が\(200{\mathrm{[{\Omega}]}}\)の時、
- 抵抗\(R_1\)と抵抗\(R_2\)と抵抗\(R_3\)の合成抵抗\(R\)は何\({\mathrm{{\Omega}}}\)でしょうか。
- 抵抗\(R_1\)に流れる電流\(I_1\)は何\({\mathrm{A}}\)でしょうか。
- 抵抗\(R_2\)に流れる電流\(I_2\)は何\({\mathrm{A}}\)でしょうか。
- 抵抗\(R_3\)に流れる電流\(I_3\)は何\({\mathrm{A}}\)でしょうか。
解答
抵抗\(R_1\)と抵抗\(R_2\)と抵抗\(R_3\)の合成抵抗\(R{\mathrm{[{\Omega}]}}\)は次式で表されます。
\begin{eqnarray}
R&=&\frac{R_1×R_2×R_3}{R_2×R_3+R_1×R_3+R_1×R_2}\\
\\
&=&\frac{10×50×200}{50×200+10×200+10×50}\\
\\
&=&8{\mathrm{[{\Omega}]}}\tag{17}
\end{eqnarray}
したがって、抵抗\(R_1\)に流れる電流\(I_1{\mathrm{[A]}}\)は以下の値になります。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_1&=&\frac{8}{10}×10\\
\\
&=&8{\mathrm{[A]}}\tag{18}
\end{eqnarray}
同様に、抵抗\(R_2\)に流れる電流\(I_2{\mathrm{[A]}}\)は以下の値になります。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_2&=&\frac{8}{50}×10\\
\\
&=&1.6{\mathrm{[A]}}\tag{19}
\end{eqnarray}
同様に、抵抗\(R_3\)に流れる電流\(I_3{\mathrm{[A]}}\)は以下の値になります。
\begin{eqnarray}
\mbox{求めたい電流}&=&\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\\
\\
{\Leftrightarrow}I_3&=&\frac{8}{200}×10\\
\\
&=&0.4{\mathrm{[A]}}\tag{20}
\end{eqnarray}
【分流の法則】抵抗がNつ並列接続されている時
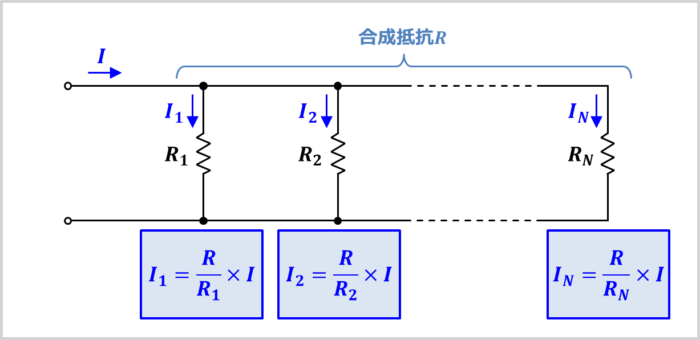

上図に抵抗\(R_1{\mathrm{[{\Omega}]}}\)、抵抗\(R_2{\mathrm{[{\Omega}]}}\)、・・・、抵抗\(R_N{\mathrm{[{\Omega}]}}\)を並列接続し、電源電圧\(V{\mathrm{[V]}}\)を印加した回路を示しています。
この回路において、並列回路に入ってくる電流を\(I{\mathrm{[A]}}\)、合成抵抗を\(R{\mathrm{[{\Omega}]}}\)とすると、各抵抗に流れる電流は
\begin{eqnarray}
\mbox{求めたい電流}=\frac{\mbox{合成抵抗}}{\mbox{求めたい電流が流れる抵抗の抵抗値}}×\mbox{並列回路に入ってくる電流}\tag{21}
\end{eqnarray}
で求めることができるので、抵抗\(R_1{\mathrm{[{\Omega}]}}\)に流れる電流\(I_1{\mathrm{[A]}}\)と抵抗\(R_2{\mathrm{[{\Omega}]}}\)に流れる電流\(I_2{\mathrm{[A]}}\)、・・・、抵抗\(R_N{\mathrm{[{\Omega}]}}\)に流れる電流\(I_N{\mathrm{[A]}}\)は次式で表されます。
\begin{eqnarray}
I_1&=&\frac{R}{R_1}×I{\mathrm{[A]}}\tag{22}\\
\\
I_2&=&\frac{R}{R_2}×I{\mathrm{[A]}}\tag{23}\\
\\
I_N&=&\frac{R}{R_N}×I{\mathrm{[A]}}\tag{24}
\end{eqnarray}
「分流の法則」と「分圧の法則」の違い
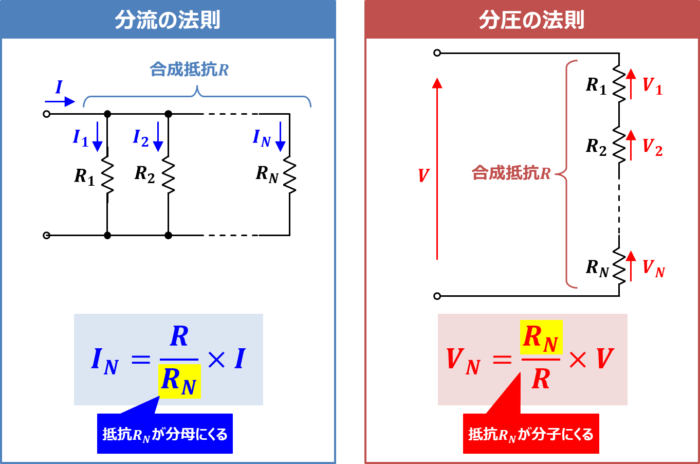

「分流の法則」と「分圧の法則」は公式が非常に似ています。
分流の法則
分流の法則は、抵抗が並列接続されている時に、各抵抗に流れる電流を求める法則です。
並列接続されている抵抗の合成抵抗を\(R{\mathrm{[{\Omega}]}}\)、並列回路に入ってくる電流を\(I{\mathrm{[A]}}\)とすると、抵抗\(R_N{\mathrm{[{\Omega}]}}\)に流れる電流\(I_N{\mathrm{[A]}}\)は次式で表されます。
\begin{eqnarray}
I_N=\frac{R}{R_N}×I{\mathrm{[A]}}\tag{25}
\end{eqnarray}
分圧の法則
分圧の法則は、抵抗が直列接続されている時に、各抵抗にかかる電圧を求める法則です。
並列接続されている抵抗の合成抵抗を\(R{\mathrm{[{\Omega}]}}\)、直列回路にかかる電圧を\(V{\mathrm{[V]}}\)とすると、抵抗\(R_N{\mathrm{[{\Omega}]}}\)にかかる電圧\(V_N{\mathrm{[V]}}\)は次式で表されます。
\begin{eqnarray}
V_N=\frac{R_N}{R}×V{\mathrm{[V]}}\tag{26}
\end{eqnarray}
(25)式と(26)式は似ていますね。「分流の法則」では抵抗\(R_N{\mathrm{[{\Omega}]}}\)が分母、「分圧の法則」では抵抗\(R_N{\mathrm{[{\Omega}]}}\)が分子にある点に注意してください。
まとめ
この記事では『分流の法則』について、以下の内容を説明しました。
- 分流の法則とは
- 分流の法則の『公式』・『公式の導出方法』・『例題』
- 「分流の法則」と「分圧の公式」の違い
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。