回路計算において、電源(電圧源や電流源)が1つのみの場合、計算は簡単です。
しかし、電源が2つ以上になると、回路計算が複雑になります。この時に役立つ法則が『重ね合わせの理』です。
この記事では『重ね合わせの理』について
- 重ね合わせの理とは
- 重ね合わせの理を用いて、回路に流れる電流を求める手順
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
重ね合わせの理とは
重ね合わせの理は、複数の電源を含む回路において、「回路の任意の部分に流れる電流(または電圧)」は「それぞれの電源を単独で存在させた回路に流れる電流(または電圧)」を重ね合わせたもの(足し合わせたもの)に等しいという法則です。
上記の文章だけでは難しそうに見えますが、下記の具体例を見れば、重ね合わせの理が理解しやすくなると思います。
具体例
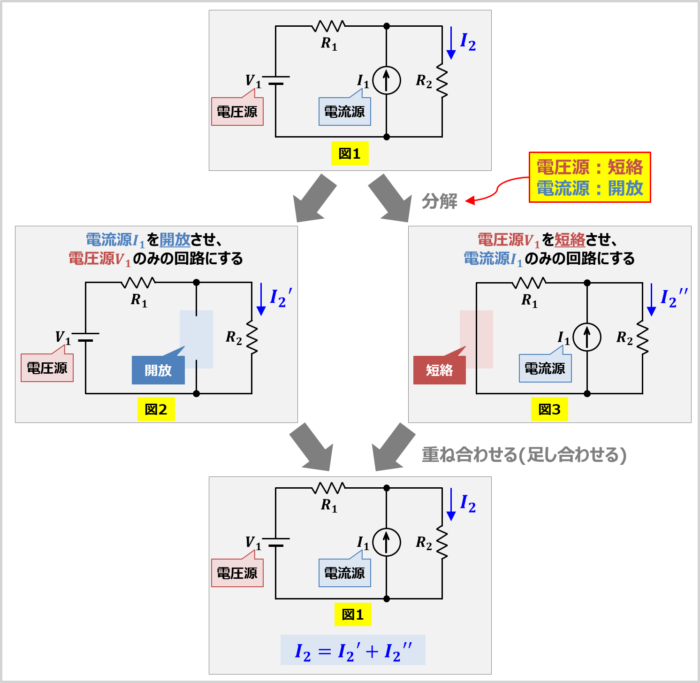
例えば、図1に示すように、『複数の電源(電圧源\(V_1\)と電流源\(I_1\))、抵抗\(R_1\)、抵抗\(R_2\)で構成された回路』があるとします。この回路において、それぞれの電源を単独で存在させた回路を考えると、図2および図3のようになります。
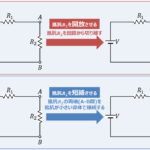
取り除く電源が電圧源の場合は短絡、電流源の場合は開放させます。
図2では電流源\(I_1\)を取り除いているので、電流源\(I_1\)を開放しています。また、図3では電圧源\(V_1\)を取り除いているので、電圧源\(V_1\)を短絡させています。
この時、
- 電圧源\(V_1\)のみの回路(図2)において、抵抗\(R_2\)に流れる電流を\(I_2'\)
- 電流源\(I_1\)のみの回路(図3)において、抵抗\(R_2\)に流れる電流を\(I_2''\)
とすると、元の回路(図1)において、抵抗\(R_2\)に流れる電流\(I_2\)は次式で表されます。
I_2=I_2'+I_2''
\end{eqnarray}
このように、重ね合わせの理では、「それぞれの電源を単独で存在させた回路に流れる電流(\(I_2'\)および\(I_2''\))」を重ね合わせる(足し合わせる)ことにより、「複数の電源を含む回路に流れる電流\(I_2\)」を求めることができるのです。
では次に、実際の回路において、回路に流れる電流を重ね合わせの理を用いて求めてみましょう。
補足
- 重ね合わせの理は、英語では「Superposition Theorem」と書きます。
- 重ね合わせの理は、「重ね合わせの定理」や「重ね合わせの原理」や「重ねの理」や「重畳の理」とも呼ばれています。
あわせて読みたい
『開放』と『短絡』については下記の記事で詳しく説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

『開放』と『短絡』の違いについて【電気回路の基礎】
続きを見る
重ね合わせの理を用いて電流を求める手順
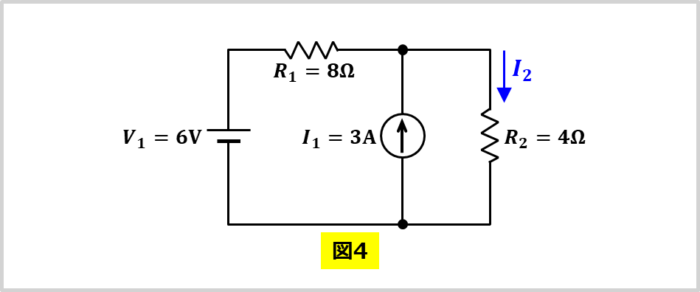

重ね合わせの理の計算例として、上図に示している『複数の電源(電圧源\(V_1\)と電流源\(I_1\))、抵抗\(R_1\)、抵抗\(R_2\)で構成された回路』において、抵抗\(R_2\)に流れる電流\(I_2\)を求めてみましょう。
抵抗\(R_2\)に流れる電流\(I_2\)は下記の手順(ステップ1~3)で求めることができます。
重ね合わせの理を用いて電流を求める手順
- 元の回路を電源ごとに分解する
- 各分解回路に流れる電流を求める
- 各分解回路に流れる電流を重ね合わせて、元の回路に流れる電流を求める
各ステップについて順番に説明します。
元の回路を電源ごとに分解する
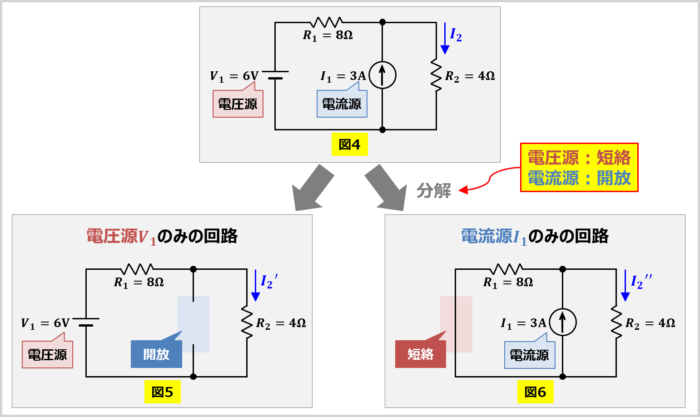

まず元の回路(図4)において、電源を1つだけ残し、それぞれの電源を単独で存在させた回路に分解します。この時、取り除く電源が電圧源の場合は短絡、電流源の場合は開放させます。
元の回路(図4)において、それぞれの電源を単独で存在させた回路に分解すると、「電圧源\(V_1\)のみの回路(図5)」および「電流源\(I_1\)のみの回路(図6)」のようになります。
各分解回路に流れる電流を求める

分解回路を作った後は、各分解回路ごとに抵抗\(R_2\)に流れる電流を求めます。
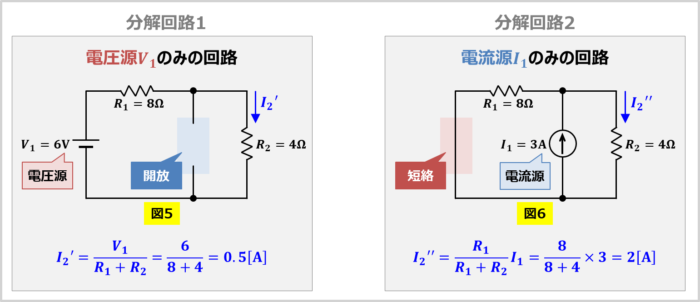
- 「分解回路1:電圧源\(V_1\)のみの回路(図5)」に流れる電流
- 「分解回路2:電流源\(I_1\)のみの回路(図6)」に流れる電流
電圧源\(V_1\)のみの回路(図5)において、抵抗\(R_2\)に流れる電流\(I_2'\)はオームの法則より以下の値となります。
\begin{eqnarray}
I_2'=\frac{V_1}{R_1+R_2}=\frac{6}{8+4}=0.5{\mathrm{[A]}}
\end{eqnarray}
電流源\(I_1\)のみの回路(図6)において、抵抗\(R_2\)に流れる電流\(I_2''\)は分流の法則より以下の値となります。
\begin{eqnarray}
I_2''=\frac{R_1}{R_1+R_2}I_1=\frac{8}{8+4}×3=2{\mathrm{[A]}}
\end{eqnarray}
各分解回路に流れる電流を重ね合わせて、元の回路に流れる電流を求める
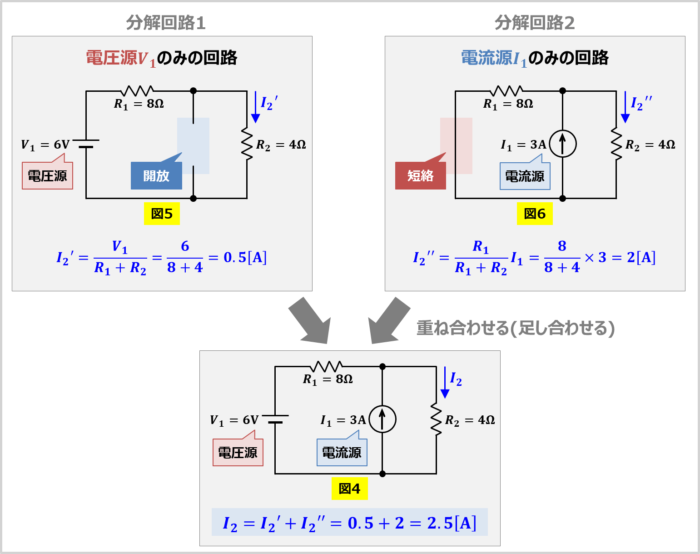

「電圧源\(V_1\)のみの回路(図5)」および「電流源\(I_1\)のみの回路(図6)」において、抵抗\(R_2\)に流れる電流を求めました。
その後は、「それぞれの電源を単独で存在させた回路に流れる電流(\(I_2'\)および\(I_2''\))」を重ね合わせる(足し合わせる)ことにより、「元の回路(図4)に流れる電流\(I_2\)」を求めます。
元の回路(図4)において、抵抗\(R_2\)に流れる電流\(I_2\)は以下の値となります。
\begin{eqnarray}
I_2=I_2'+I_2''=0.5+2=2.5{\mathrm{[A]}}
\end{eqnarray}
このように、重ね合わせの理を使うと、複数の電源がある回路でも、電源を1つだけにして回路計算ができるので、キルヒホッフの法則などを使うよりも、簡単に計算することができる場合が多いです。
まとめ
この記事では『重ね合わせの理』について、以下の内容を説明しました。
- 重ね合わせの理とは
- 重ね合わせの理を用いて、回路に流れる電流を求める手順
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。