この記事では『電圧源』について
- 電圧源とは
- 負荷にかかる電圧(電圧源の内部抵抗rをゼロとした時)
- 負荷にかかる電圧(電圧源の内部抵抗rを考慮した時)
- 電圧源の記号
- 電圧源に流れる電流
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
電圧源とは
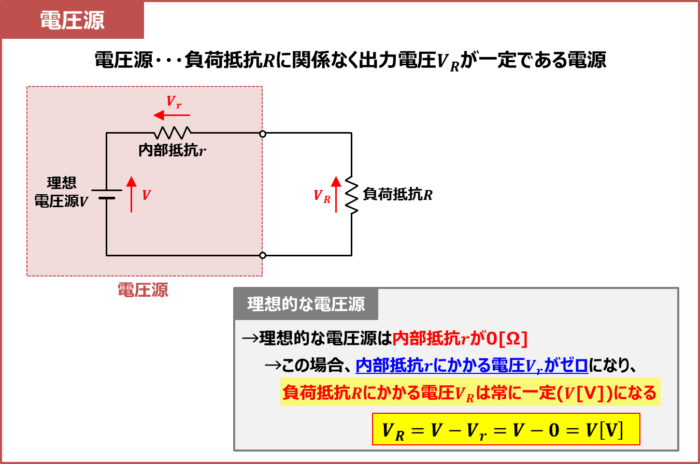
電圧源は、負荷抵抗\(R\)に関係なく出力電圧\(V_R\)が一定である電源です。
電圧源は「理想電圧源\(V\)(一定の電圧を出力する電源)」と「内部抵抗\(r\)」を直列接続した回路で表されます。
内部抵抗\(r\)が0[Ω]の電圧源が理想的な電圧源となります。この場合、内部抵抗\(r\)にかかる電圧\(V_r\)がゼロになり、負荷抵抗\(R\)にかかる電圧\(V_R\)は次式で表されます。
\begin{eqnarray}
V&=&V_r+V_R\\
\\
{\Leftrightarrow}V_R&=&V-V_r\\
\\
&=&V-0\\
\\
&=&V{\mathrm{[V]}}\tag{1}
\end{eqnarray}
(1)式には、負荷抵抗\(R\)がありません。そのため、理想的な電圧源の場合、負荷抵抗\(R\)にかかる電圧\(V_R\)は負荷抵抗\(R\)の大きさに関わらず常に一定(\(V{\mathrm{[V]}}\))になることが分かります。
ポイント
- 理想的な電圧源は内部抵抗\(r\)が0[Ω]である。
- この場合、負荷抵抗\(R\)にかかる電圧\(V_R\)は負荷抵抗\(R\)の大きさに関わらず常に一定になる。
では、次に、内部抵抗\(r\)を考慮した時において、負荷抵抗\(R\)にかかる電圧\(V_R\)がどのようになるかを考えてみましょう。
負荷にかかる電圧(電圧源の内部抵抗rを考慮した時)
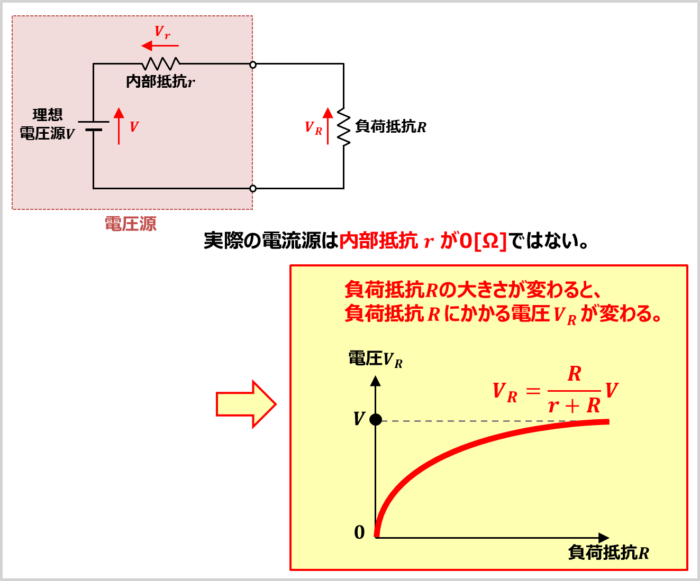
実際の電圧源は、内部抵抗\(r\)が0[Ω]ではありません。この場合、「理想電圧源\(V\)(一定の電圧を出力する電源)」は内部抵抗\(r\)と負荷抵抗\(R\)で分圧するため、負荷抵抗\(R\)にかかる電圧\(V_R\)は次式となります。
\begin{eqnarray}
V_R=\frac{R}{r+R}V{\mathrm{[V]}}\tag{2}
\end{eqnarray}
(2)式には、負荷抵抗\(R\)があります。そのため、負荷抵抗\(R\)の大きさが変わると、負荷抵抗\(R\)にかかる電圧\(V_R\)が変わってしまいます。
なお、理想的な電圧源の場合、内部抵抗\(r\)が0[Ω]なので、負荷抵抗\(R\)にかかる電圧\(V_R\)は次式に近似することができます。
\begin{eqnarray}
V_R&=&\frac{R}{r+R}V\\
\\
&{\approx}&\frac{R}{0+R}V\\
\\
&{\approx}&V{\mathrm{[V]}}\tag{3}
\end{eqnarray}
内部抵抗\(r\)が0[Ω]の場合、式から負荷抵抗\(R\)が消えます。そのため、理想的な電圧源の場合、負荷抵抗\(R\)にかかる電圧\(V_R\)は負荷抵抗\(R\)の大きさに関わらず常に一定(\(V{\mathrm{[V]}}\))になることが分かります。
電圧源の記号
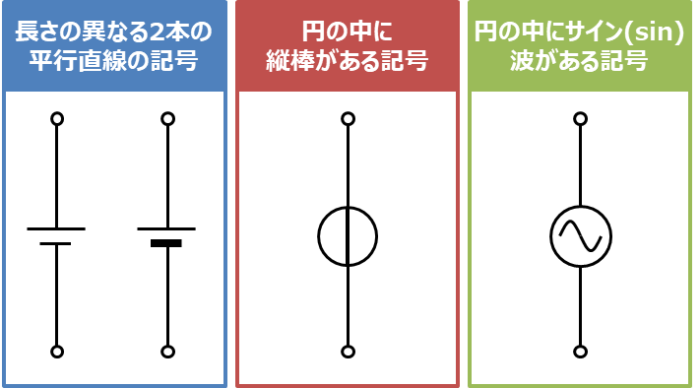
電圧源は上図に示すような記号が使われます。直流の場合は「長さの異なる2本の平行直線の記号」、交流の場合は「円の中にサイン(sin)波がある記号」がよく使われます。各記号について下記に説明します。
- 長さの異なる2本の平行直線の記号
- 円の中に縦棒がある記号
- 円の中にサイン(sin)波がある記号
長い方の直線がプラス(+)端子、短い方の直線がマイナス(-)端子となります。短い方の直線を少し太く描くこともありますが、長さの違いが分かれば、極性が分かるので、太くしなくても問題ありません。
「JIS C 0617」に記載されている理想電圧源の記号です。直流と交流の両方で使用されます。極性などのパラメータは記号の近くに表記します。
交流の電圧源を表します。
電圧源に流れる電流
理想的な電圧源の場合、負荷抵抗\(R\)にかかる電圧\(V_R\)は負荷抵抗\(R\)に関わらず一定となります。
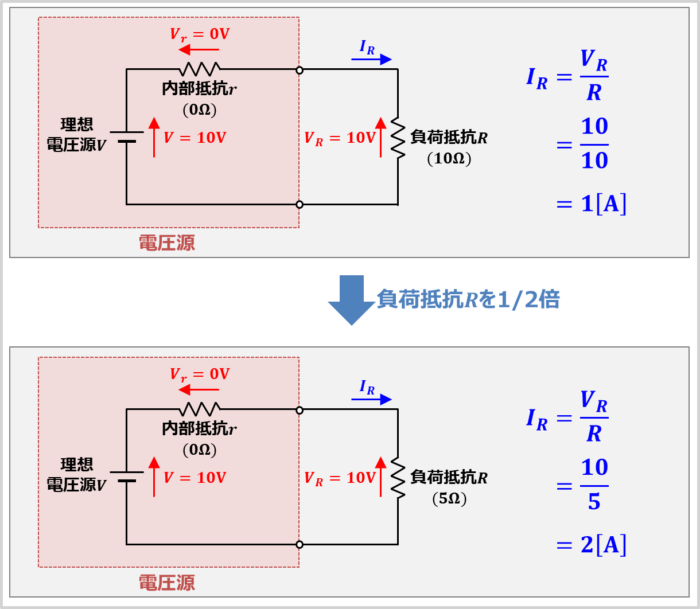
そのため、例えば、10Vの電圧を出力する電圧源に10Ωの負荷抵抗\(R\)を接続した場合、負荷抵抗\(R\)に流れる電流(電圧源に流れる電流)\(I_R\)は以下の値となります。
\begin{eqnarray}
I_R=\frac{V}{R}=\frac{10}{10}=1{\mathrm{[A]}}\tag{4}
\end{eqnarray}
負荷抵抗\(R\)が1/2倍の5Ωになると、電圧源に流れる電流\(I_R\)が2倍となり、以下の値となります。
\begin{eqnarray}
I_R=\frac{V}{R}=\frac{10}{5}=2{\mathrm{[A]}}\tag{5}
\end{eqnarray}
このように、電圧源に流れる電流\(I_R\)は負荷抵抗\(R\)が小さくなるにつれて増加します。
電圧源にかかる電圧(負荷抵抗\(R\)を短絡した場合)
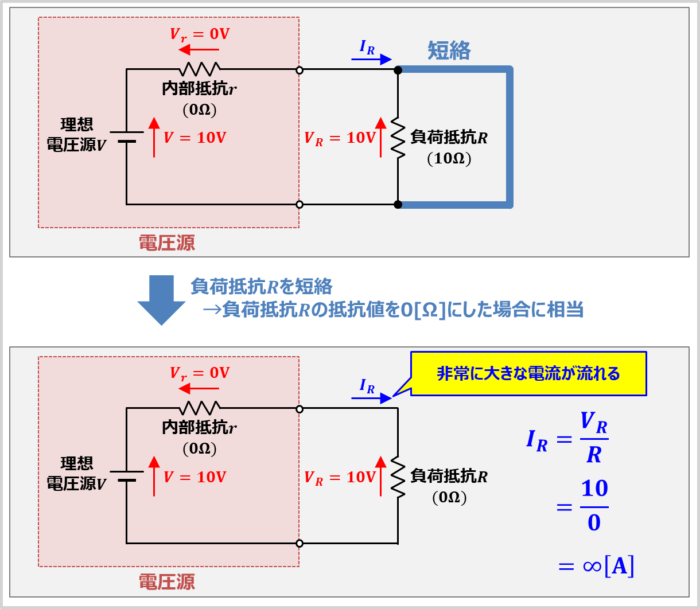
では、10Vの電圧を出力する電圧源に接続されている負荷抵抗\(R\)を短絡した時はどうなるでしょうか。
負荷抵抗\(R\)を短絡したということは、負荷抵抗\(R\)の抵抗値を0[Ω]にした場合に相当します。
この場合、計算上、電圧源に流れる電流\(I_R\)は以下の値となり、非常に大きな電流が流れてしまいます。
\begin{eqnarray}
I_R=\frac{V}{R}=\frac{10}{0}=∞{\mathrm{[A]}}\tag{6}
\end{eqnarray}
したがって、電圧源を使用する場合には、電圧源に接続する負荷は短絡しないように注意しなければいけません。
あわせて読みたい
負荷の『短絡』については、下記の記事で別途説明しています。興味のある方は下記のリンクからぜひチェックをしてみてください。
-

『開放』と『短絡』の違いについて【電気回路の基礎】
続きを見る
まとめ
この記事では『電圧源』について、以下の内容を説明しました。
- 電圧源とは
- 負荷にかかる電圧(電圧源の内部抵抗rをゼロとした時)
- 負荷にかかる電圧(電圧源の内部抵抗rを考慮した時)
- 電圧源の記号
- 電圧源に流れる電流
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。