この記事では『等価直列抵抗(ESR)』と『等価直列インダクタンス(ESL)』について
- コンデンサの『等価回路』
- 『等価直列抵抗(ESR)』とは
- 『等価直列インダクタンス(ESL)』とは
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
コンデンサの『等価回路』
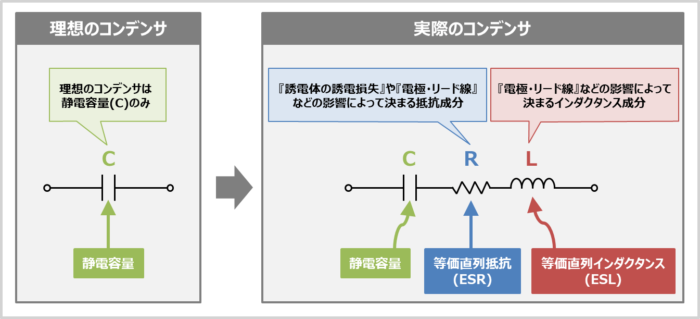
理想のコンデンサは静電容量(C)のみですが、実際のコンデンサは抵抗成分(R)やインダクタンス成分(L)を含んでます。そのため、コンデンサはC・R・Lが直列接続されている等価回路で表現することができます。この抵抗成分(R)のことを等価直列抵抗(ESR)、インダクタンス成分(L)のことを等価直列インダクタンス(ESL)といいます。
したがって、実際のコンデンサのインピーダンス\({\dot{Z}}\)は次式で表すことができます。
\begin{eqnarray}
{\dot{Z}}&=&R+j{\omega}L+\frac{1}{j{\omega}C}\\
\\
&=& R+j2{\pi}fL+\frac{1}{j2{\pi}fC}
\end{eqnarray}
また、インピーダンスの大きさZは上式の絶対値となるため、次式で表すことができます。
\begin{eqnarray}
Z&=&|{\dot{Z}}|\\
\\
&=&\sqrt{R^2+\left({\omega}L-\frac{1}{{\omega}C}\right)^2}\\
\\
&=&\sqrt{R^2+\left(2{\pi}fL-\frac{1}{2{\pi}fC}\right)^2}
\end{eqnarray}
上式において、各記号は以下の意味を表しています。
- \({\dot{Z}}\):インピーダンス[Ω]
- \(Z\):インピーダンスの大きさ[Ω]
- \(R\):等価直列抵抗(ESR)[Ω]
- \(j\):虚数単位
- \(L\):等価直列インダクタンス(ESL)[H]
- \(C\):静電容量[F]
- \({\omega}\):角周波数[rad/s](=2πf)
- \(f\):周波数[Hz]
次に『等価直列抵抗(ESR)』と『等価直列インダクタンス(ESL)』について詳しく説明します。
『等価直列抵抗(ESR)』とは
等価直列抵抗(ESR)は『誘電体の誘電損失』や『電極・リード線』などの影響によって決まる抵抗成分Rです。ESRが大きいと、コンデンサに電流Iが流れることによる損失RI2によって発熱が大きくなります。
また、ESRは『Equivalent Series Resistance』の略となっています。
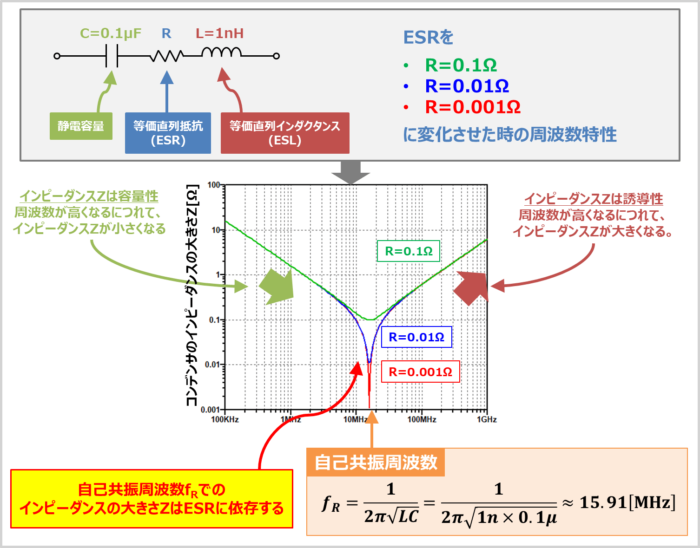
ここで一例として、静電容量が『C=0.1μF』、ESLが『L=1nH』のコンデンサにおいて、ESRが『R=0.1Ω、0.01Ω、0.001Ω』に変化した時の影響を見てみましょう。
上図に示しているのは『コンデンサのインピーダンスZの周波数特性(周波数fが変化した時のインピーダンスZの変化を表す特性)』です。横軸が周波数f、縦軸がインピーダンスZとなっています。なお、横軸も縦軸も対数軸にしています。
コンデンサの「自己共振周波数fR」は以下の値となります。
\begin{eqnarray}
f_R&=&\frac{1}{2{\pi}\sqrt{LC}}\\
\\
&=&\frac{1}{2{\pi}\sqrt{1×10^{-9}×0.1×10^{-6}}}\\
\\
&{\approx}&15.91{\mathrm{[MHz]}}
\end{eqnarray}
自己共振周波数fRまではインピーダンスZは容量性であり、周波数が高くなるにつれて、インピーダンスZが小さくなります。
自己共振周波数fRを過ぎると、インピーダンスZは誘導性であり、周波数が高くなるにつれて、インピーダンスZが大きくなります。
また、自己共振周波数fRではコンデンサのインピーダンスZは次式で表されます。
\begin{eqnarray}
Z&=&\sqrt{R^2+\left(2{\pi}f_RL-\frac{1}{2{\pi}f_RC}\right)^2}\\
\\
&=&\sqrt{R^2+\left(2{\pi}\frac{1}{2{\pi}\sqrt{LC}}L-\frac{1}{2{\pi}\displaystyle\frac{1}{2{\pi}\sqrt{LC}}C}\right)^2}\\
\\
&=&\sqrt{R^2+\left(\sqrt{\displaystyle\frac{L}{C}}-\frac{1}{\sqrt{\displaystyle\frac{C}{L}}}\right)^2}\\
\\
&=&\sqrt{R^2+0^2}\\
\\
&=&R
\end{eqnarray}
すなわち、自己共振周波数fRでのインピーダンスの大きさZはESRに依存するということです(言い換えれば、インピーダンスの大きさZの下限はESRで決まるということです)。そのため、ESRが大きいほど自己共振周波数fR付近でのインピーダンスZが大きくなります。
補足
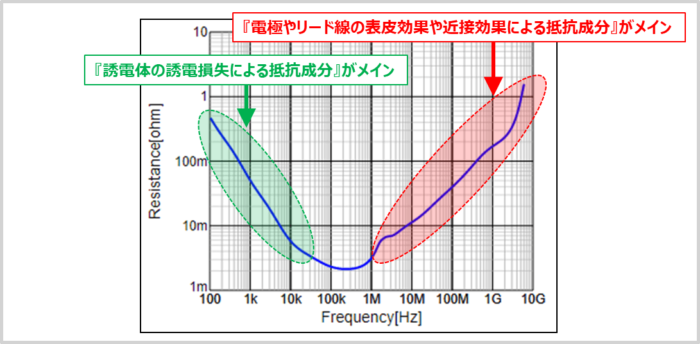
- 等価直列抵抗(ESR)は等価回路上では一定値になっていますが、実際には周波数により変化します。低周波領域では『誘電体の誘電損失による抵抗成分』がメインであり、高周波領域では、『電極やリード線の表皮効果や近接効果による抵抗成分』がメインとなります。下図に村田製作所製のセラミックコンデンサ(GRMシリーズ)の『ESRの周波数特性(縦軸:ESR、横軸:周波数)』を示しています(型番により周波数特性が異なるので、詳しくは各メーカーのデータシートや仕様書等を確認してください)。周波数によりESRが変化していることが分かります。
『等価直列インダクタンス(ESL)』とは
等価直列インダクタンス(ESL)は『電極・リード線』などの影響によって決まるインダクタンス成分Lです。後ほど詳しく説明しますが、ESLが大きいと、高周波領域でのインピーダンスが大きくなります。
ESLは『Equivalent Series Inductance』なので『ESI』なのでは?と思うかもしれません。なぜ『ESI』ではなく『ESL』なのでしょうか。
それは、インダクタンス(Inductance)の記号が「L」だからです。インダクタンスの記号を『I』にすると、電流と混同してしまいます。インダクタンスの記号を『L』で表す由来としては、様々な説がありますが、レンツの法則を解明した(Lenz)の頭文字の『L』をとったという説が有力です。
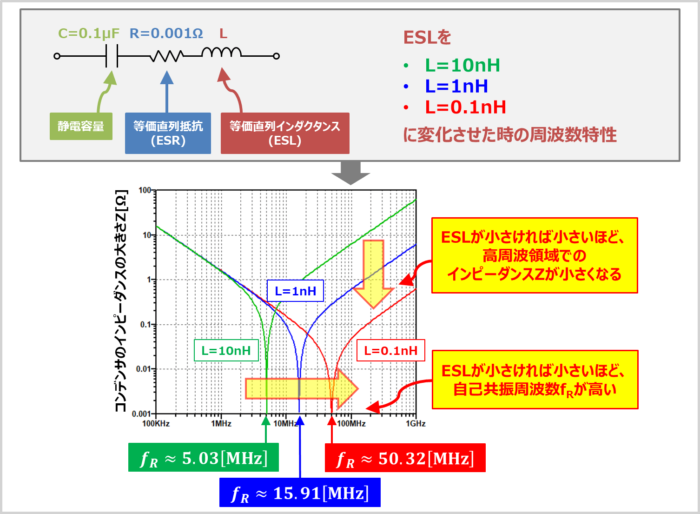
ここで一例として、静電容量が『C=0.1μF』、ESRが『R=0.001Ω』のコンデンサにおいて、ESLが『L=10nH、1nH、0.1nH』に変化した時の影響を見てみましょう。
上図に示しているのは『コンデンサのインピーダンスZの周波数特性』です。横軸が周波数f、縦軸がインピーダンスZとなっています。なお、横軸も縦軸も対数軸にしています。
各ESLにおける「自己共振周波数fR」は以下の値となります。
- L=10nHの時
- L=1nHの時
- L=0.1nHの時
\begin{eqnarray}
f_R=\frac{1}{2{\pi}\sqrt{LC}}=\frac{1}{2{\pi}\sqrt{10×10^{-9}×0.1×10^{-6}}}{\;}{\approx}{\;}5.03{\mathrm{[MHz]}}
\end{eqnarray}
\begin{eqnarray}
f_R=\frac{1}{2{\pi}\sqrt{LC}}=\frac{1}{2{\pi}\sqrt{1×10^{-9}×0.1×10^{-6}}}{\;}{\approx}{\;}15.91{\mathrm{[MHz]}}
\end{eqnarray}
\begin{eqnarray}
f_R=\frac{1}{2{\pi}\sqrt{LC}}=\frac{1}{2{\pi}\sqrt{0.1×10^{-9}×0.1×10^{-6}}}{\;}{\approx}{\;}50.32{\mathrm{[MHz]}}
\end{eqnarray}
このように、ESLが小さければ小さいほど、自己共振周波数fRが高くなります。また、高周波領域でのインピーダンスZが小さくなります。すなわち、コンデンサの性能を高い周波数まで有効に働かせるためには、ESLを小さくすることが重要ということになります。
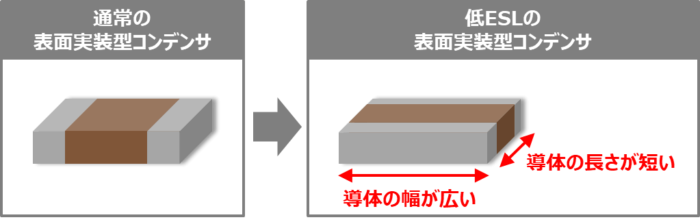
一般的には導体の幅を広くし、導体の長さを短くすればインダクタンスが小さくなるため、下図に示すように縦横を逆にした低ESLの表面実装型コンデンサも商品としてあります。
まとめ
この記事では『等価直列抵抗(ESR)』と『等価直列インダクタンス(ESL)』について、以下の内容を説明しました。
- コンデンサの『等価回路』
- 『等価直列抵抗(ESR)』とは
- 『等価直列インダクタンス(ESL)』とは
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。






