【インピーダンスとは】『単位』や『計算方法』などのまとめ！

インピーダンスは電流を妨げるものの総称であり、直流と交流両方の電気の流れを妨げる『抵抗(レジスタンス)』と交流のみ電気の流れを妨げる『リアクタンス』を合わせたものです。

この記事ではこのインピーダンスについて

インピーダンスとは
インピーダンスの特徴
インピーダンスに関する例題

などを図を用いて分かりやすく説明しています。

インピーダンスとは

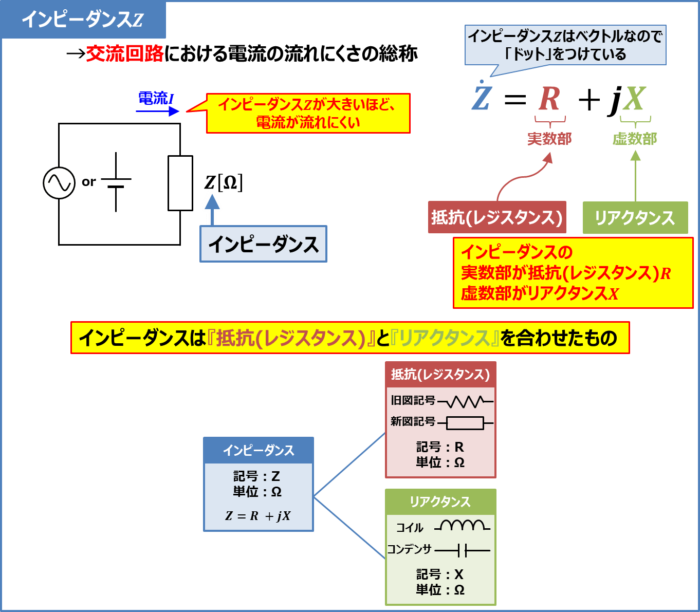
最初にインピーダンスの要点を以下にまとめます。

インピーダンスの要点

インピーダンスは『抵抗(レジスタンス)』と『リアクタンス』を合わせたものである
インピーダンスは「電流の流れにくさを表すもの」であり、記号はZ、単位は[Ω]を用いる
インピーダンスが大きいほど電流が流れにくくなる
インピーダンス(Z=R+jX)の実数部が『抵抗(レジスタンス)』、虚数部が『リアクタンス』である

各要点について順番に説明します。

インピーダンスは『抵抗(レジスタンス)』と『リアクタンス』を合わせたものである

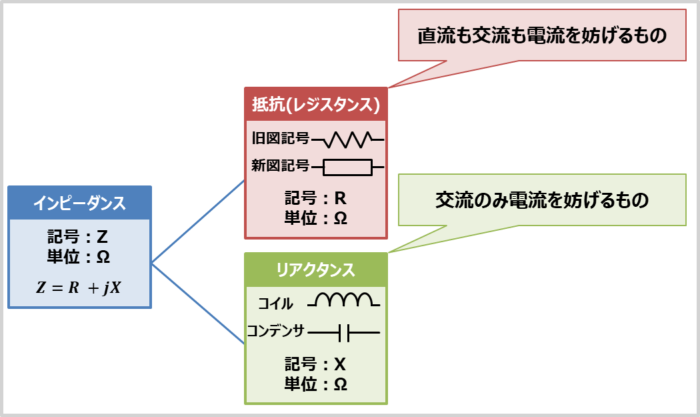
インピーダンスは『抵抗(レジスタンス)』と『リアクタンス』を合わせたものです。

少し言い方を変えると、電流を妨げるものの総称が『インピーダンス』であり、インピーダンスの中で直流も交流も電流を妨げるものが『抵抗(レジスタンス)』であり、交流のみ電流を妨げるものが『リアクタンス』ということになります。

インピーダンスは「電流の流れにくさを表すもの」であり、記号はZ、単位は[Ω]を用いる

インピーダンスは「電流を妨げるものの総称」です。

抵抗Rも「電流の流れにくさ」を表すものですが、抵抗Rは「直流回路と交流回路の両方における電流の流れにくさ」を表すものです。また、「抵抗R、電流I、電圧Vの関係」はオームの法則より次式で表されます。

\begin{eqnarray}
R=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

オームの法則は交流回路でも使用することができ、「インピーダンスZ、電流I、電圧Vの関係」を式で表すと次式で表されます。

\begin{eqnarray}
Z=\frac{V}{I}{\mathrm{[{\Omega}]}}
\end{eqnarray}

例えば、交流電圧源の電圧Vが10[V]であり、この時に流れている電流Iが5[A]の場合、インピーダンスZは2[Ω]となります。

また、インピーダンスZ[Ω]と電圧V[V]が分かれば電流I[A]を求めることができ、インピーダンスZ[Ω]と電流I[A]が分かれば電圧V[V]を求めることができます。

インピーダンスZ[Ω]と電圧V[V]が分かっている時

\begin{eqnarray}
I=\frac{V}{Z}{\mathrm{[A]}}
\end{eqnarray}

インピーダンスZ[Ω]と電流I[A]が分かっている時

\begin{eqnarray}
V=ZI{\mathrm{[V]}}
\end{eqnarray}

インピーダンスが大きいほど電流が流れにくくなる

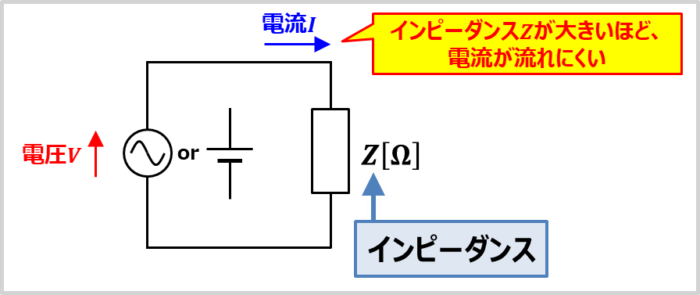
インピーダンスZは「電流の流れにくさ」を表しています。そのため、インピーダンスZの大きさにより電流Iは以下のように変わります。

インピーダンスZが大きい

→電流Iが流れにくい

インピーダンスZが小さい

→電流Iが流れやすい

また、インピーダンスZ[Ω]と電圧V[V]が分かっている時、流れる電流I[A]は「\(I=\displaystyle\frac{V}{Z}{\mathrm{[A]}}\)」であることを説明しました。この式からインピーダンスZ[Ω]が大きくなると、電流Iが小さくなることが分かりますね。

インピーダンスの実数部が『抵抗(レジスタンス)』、虚数部が『リアクタンス』である

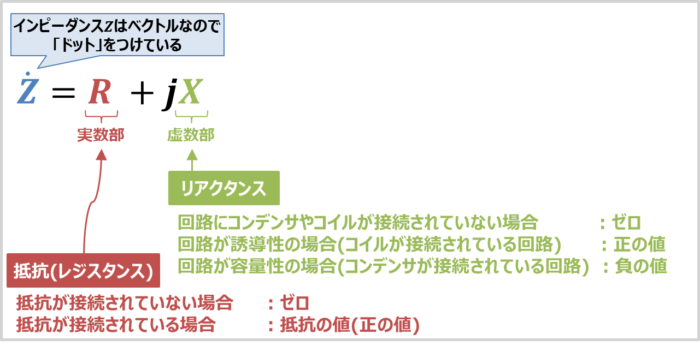
インピーダンスZは抵抗(レジスタンス)RとリアクタンスXを用いると次式で表されます。

\begin{eqnarray}
{\dot{Z}}=R+jX
\end{eqnarray}

なお、抵抗(レジスタンス)Rは『ゼロ』または『正の値』となります。抵抗が接続されていない場合はゼロとなり、抵抗が接続されている場合は抵抗値の値(正の値)となります。

一方、リアクタンスXは『ゼロ』または『正の値』または『負の値』となります。回路にコイルやコンデンサが接続されていない場合はゼロとなります。また、回路が誘導性の場合(コイルが接続されている回路)は正の値となり、回路が容量性の場合(コンデンサが接続されている回路)は負の値となります。

RLC直列回路のインピーダンス

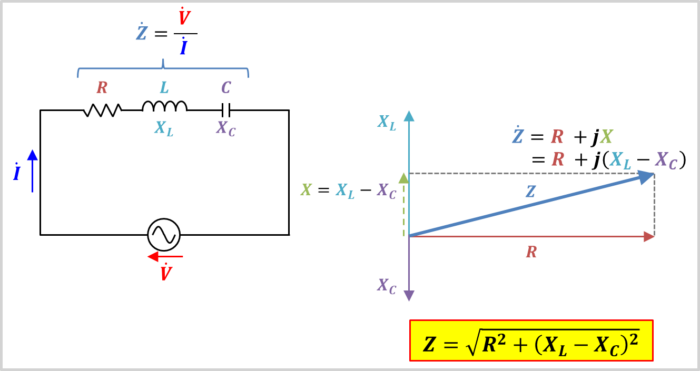
ここで一例として、RLC直列回路のインピーダンスについて説明します。

上図に示すように、抵抗R、コイルL、コンデンサCが直列接続されているRLC直列回路に対して、交流電源\({\dot{V}}\)を接続した時に回路に流れる電流が\({\dot{I}}\)だったとします。なお、交流電源\({\dot{V}}\)の大きさを\(V\)、電流\({\dot{I}}\)の大きさを\(I\)とします。

この時の、電圧\({\dot{V}}\)と電流\({\dot{I}}\)の比がRLC直列回路のインピーダンス\({\dot{Z}}\)となり、下記の式となります。

\begin{eqnarray}
{\dot{Z}}=\frac{{\dot{V}}}{{\dot{I}}}
\end{eqnarray}

なお、インピーダンスの大きさ\(Z\)は、下記の式となります。

\begin{eqnarray}
Z=\frac{V}{I}
\end{eqnarray}

ここで、RLC直列回路のインピーダンスの大きさ\(Z\)を求めてみましょう。

まず、インピーダンスベクトル\({\dot{Z}}\)を描きます。下記の手順で描きましょう。

実軸上に抵抗Rのベクトルを描く

向きは右方向、ベクトルの長さは抵抗Rの大きさになります。

虚軸上にコイルLのベクトルを描く

向きは上方向、ベクトルの長さはコイルLの誘導性リアクタンスX_Lの大きさになります。

虚軸上にコンデンサCのベクトルを描く

向きは下方向、ベクトルの長さはコンデンサCの容量性リアクタンスX_Cの大きさになります。

なお、誘導性リアクタンスXLと容量性リアクタンスXCの差を合成リアクタンスといい、次式で表されます。

\begin{eqnarray}
X=X_L-X_C
\end{eqnarray}

誘導性リアクタンスX_Lが容量性リアクタンスX_Cよりも大きい場合はインピーダンスは誘導性になり、誘導性リアクタンスX_Lが容量性リアクタンスX_Cよりも小さい場合はインピーダンスは容量性になります。

インピーダンスベクトル\({\dot{Z}}\)の描き方はこれで終わりです。描いたインピーダンスベクトルを式で表すと次式で表されます。

\begin{eqnarray}
{\dot{Z}}=R+j(X_L-X_C)
\end{eqnarray}

インピーダンスの大きさ\(Z\)は三平方の定理より次式で表されます。

\begin{eqnarray}
Z=\sqrt{R^2+(X_L-X_C)^2}
\end{eqnarray}

上式において、(X_L-X_C)は誘導性リアクタンスX_Lが容量性リアクタンスX_Cよりも小さい場合にはマイナスになりますが、2乗するので特に気にしなくても大丈夫です。

インピーダンスに関する例題

例題

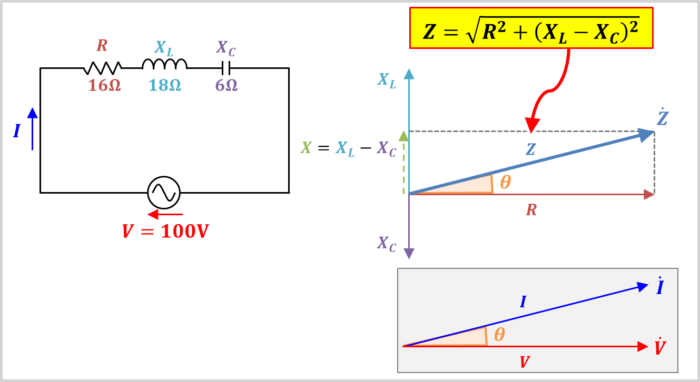
上図に示す回路において、以下のものを求めてみましょう。

インピーダンスの大きさZ
回路に流れる電流の大きさI
交流電圧源Eと回路に流れる電流Iの位相差θ

解答

インピーダンスの大きさZ

インピーダンスの大きさZは以下の値となります。

\begin{eqnarray}
Z&=&\sqrt{R^2+(X_L-X_C)^2}\\
&=&\sqrt{16^2+(18-6)^2}\\
&=&20{\mathrm{[{\Omega}]}}
\end{eqnarray}

回路に流れる電流I

回路に流れる電流の大きさIは以下の値となります。

\begin{eqnarray}
I&=&\frac{V}{Z}\\
&=&\frac{100}{20}\\
&=&5{\mathrm{[A]}}
\end{eqnarray}

交流電圧源Eと回路に流れる電流Iの位相差θ

交流電圧源Eと回路に流れる電流Iの位相差θは次式で求めることができます。

\begin{eqnarray}
{\theta}&=&{\tan}^{-1}\frac{X_L-X_C}{R}\\
&=&{\tan}^{-1}\frac{18-6}{16}\\
&=&{\tan}^{-1}\frac{3}{4}\\
&{\approx}&0.64{\mathrm{[rad]}}\\
&{\approx}&0.64×\frac{180}{{\pi}}\\
&{\approx}&37°
\end{eqnarray}

まとめ

この記事では『インピーダンス』について、以下の内容を説明しました。