この記事では『標準偏差』について
- 標準偏差とは
- 標準偏差の求め方と例題
- 標準偏差がある理由
- 標準偏差の記号
- 『標準偏差』と『分散』の違い
などを図を用いて分かりやすく説明しています。
標準偏差とは
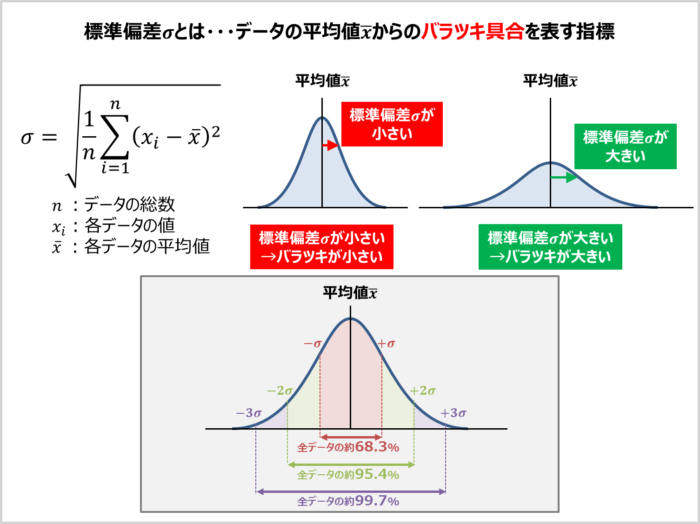
標準偏差\({\sigma}\)とはデータの平均値\(\overline{x}\)からのバラツキ具合を表す指標です。データのバラツキが大きいと標準偏差が大きくなり、バラツキが小さいと標準偏差は小さくなります。
また、データが正規分布になっている場合は平均値を中心として
- 標準偏差1つ分の範囲には全データの約68.3%
- 標準偏差2つ分の範囲には全データの約95.4%
- 標準偏差3つ分の範囲には全データの約99.7%
含まれているということも分かります。
次に、標準偏差を求める式について説明します。
補足
- 標準偏差は英語では『Standard Deviation』と書きます。頭文字を取って『SD』と略されることもあります。
標準偏差の求め方

標準偏差\({\sigma}\)は「各データの値\(x_i\)」と「データの平均値\(\overline{x}\)」の差の2乗を合計し、データの総数\(n\)で割り、平方根を取ることで求めることができます。式で表すと下記となります。
『標準偏差』を求める式
\begin{eqnarray}
{\sigma}=\sqrt{\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}
\end{eqnarray}
なお、平方根を取る前の値を「分散」といいます。「分散」は下記の式で求めることができます。
『分散』を求める式
\begin{eqnarray}
{\sigma}^2=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2
\end{eqnarray}
では簡単な例を用いて、実際に標準偏差を計算してみましょう!
標準偏差を求めてみよう!
例題として、下記の表に示している4人(A,B,C,D)のテストの点数の標準偏差を求めてみます。
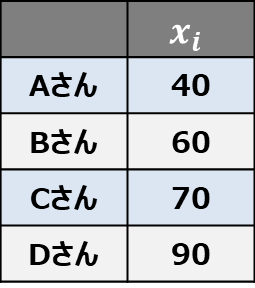
標準偏差を求める手順を下記に示します。
標準偏差を求める手順
- データ全体の平均値を求める
- 偏差(各データの値から平均値を引いた値)を求める
- 偏差を2乗する
- 偏差の2乗の合計を出す
- 偏差の合計をデータの総数で割って『分散』を求める
- 分散の平方根を取り『標準偏差』を求める
標準偏差は上記の手順に沿って計算すれば、簡単に求めることができます。次に各手順について図を用いて詳しく説明します。
データ全体の平均値を求める

まず、データ全体の平均値\(\overline{x}\)を求めます。平均値\(\overline{x}\)は各データの値を合計して、データの総数\(n\)で割ることで求めることができます。
例題ではデータの総数\(n\)は4となります(4人のテストの点数の標準偏差を求めるため)。
平均値\(\overline{x}\)を計算すると、下記の値となります。
\begin{eqnarray}
{\overline{x}}=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^nx_i=\displaystyle\frac{1}{4}\left(40+60+70+90\right)=65
\end{eqnarray}
偏差(各データの値から平均値を引いた値)を求める

次に偏差を求めます。
偏差とは「各データの値\(x_i\)から平均値\(\overline{x}\)を引いた値」のことです。
各データの値\(x_i\)から「1.データ全体の平均値を求める」で求めた平均値(65)を引くことで偏差を求めることができます。
偏差を2乗する
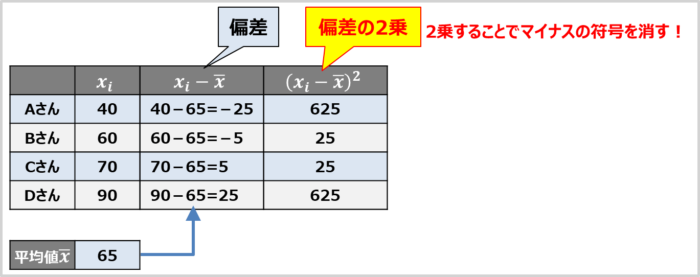
「2.偏差(各データの値から平均値を引いた値)を求める」で求めた偏差を2乗します。
偏差の2乗の合計を出す
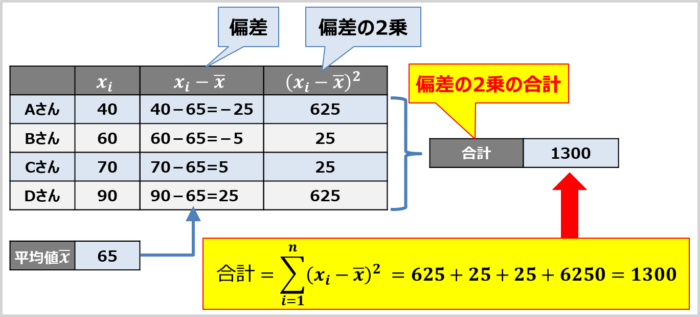
「3.偏差を2乗する」で求めた偏差の2乗を合計します。
偏差の2乗の合計は「625+25+25+625=1300」となります。
偏差の合計をデータの総数で割って『分散』を求める
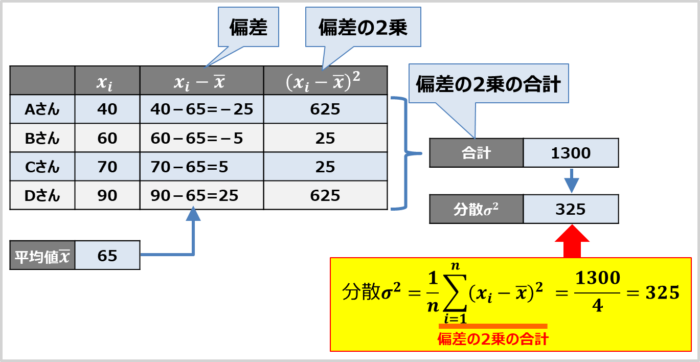
「4.偏差の2乗の合計を出す」で求めた偏差の2乗の合計(1300)をデータの総数\(n\)(今回は\(n=4\))で割ると、325になります。この値が「分散」となります。
分散の平方根を取り『標準偏差』を求める
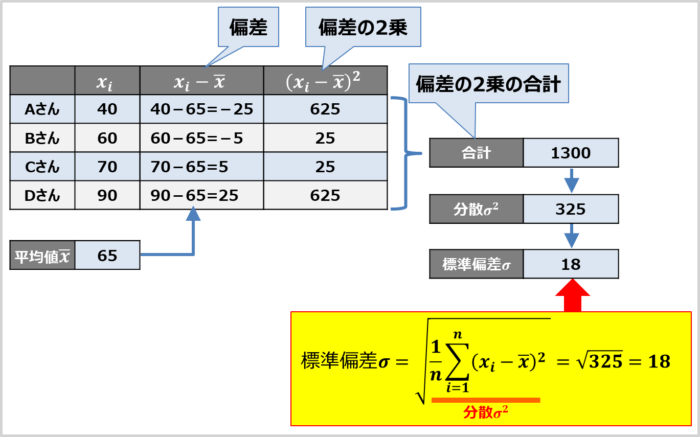
「5.偏差の合計をデータの総数で割って分散を求める」で求めた分散(325)の平方根を計算すると、下記の値となります。
\begin{eqnarray}
\sqrt{325}{\;}{\approx}{\;}18
\end{eqnarray}
したがって、「4人のテストの点数の標準偏差は約18点」であるということが分かります。
ここで、なぜ標準偏差という指標があるの?なんの役に立つの?と思う方がいると思います。次にこの疑問について解説します。
標準偏差を求める理由
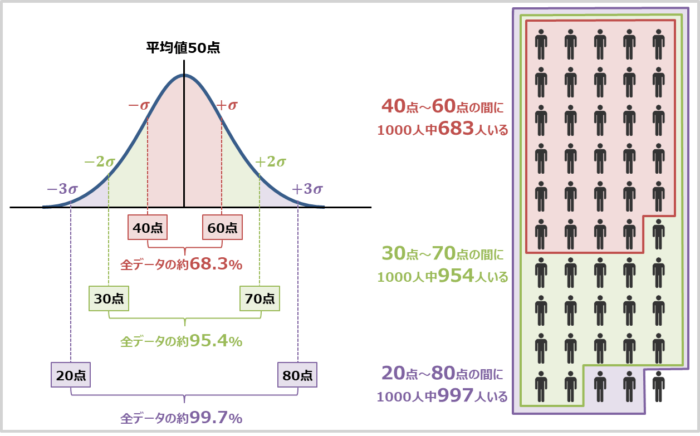
標準偏差を求める理由は「平均値から標準偏差の範囲内にどれくらいデータが含まれているのか」が分かるからです。
先ほど4人(A,B,C,D)のテストの点数を用いて『平均値』や『標準偏差』を求めました。平均値が65点、標準偏差が約18点となりましたね。標準偏差の計算方法を説明するために、データの総数\(n\)を少なくして説明しました。
次に、一例として、1000人のテストの点数の平均値が50点、標準偏差が10点であるとしましょう。
これらのテストの点数が正規分布であれば、平均値を中心として
- 標準偏差1つ分の範囲には全データの約68.3%
- 標準偏差2つ分の範囲には全データの約95.4%
- 標準偏差3つ分の範囲には全データの約99.7%
含まれていると予想することができるのです。
今回の例だと、
- 40点~60点の範囲(標準偏差1つ分の範囲)の間に1000人中683人(68.3%)
- 30点~70点の範囲(標準偏差2つ分の範囲)の間に1000人中954人(95.4%)
- 20点~80点の範囲(標準偏差3つ分の範囲)の間に1000人中997人(99.7%)
含まれているということが標準偏差から予想することができます。
『標準偏差』と『分散』の違い
『標準偏差』も『分散』もデータのバラツキ具合を表す指標となります。
「標準偏差を求めてみよう!」の章で説明しましたが、標準偏差は分散に対して平方根を取ることで求めることができます。そのため、標準偏差か分散のどちらかが分かれば、もう一方を導出することができます。
では、『標準偏差』と『分散』の違いはなんでしょうか?
大きな違いは標準偏差は各データの単位と次元が同じなのに対して、分散は各データの単位と次元が違う点です。
例えば、1000人の身長を「cm」の単位で測定した場合を考えてみましょう。
平均値の単位は「cm」、標準偏差の単位も「cm」となります。一方、分散の単位は「cm」の2乗の「cm2」となるので、平均値や標準偏差と次元が異なります。次元が異なるので、平均値と分散の値を比較したり、計算したりすることができません。
標準偏差は各データの単位と次元が同じなので比較や計算をすることができます。
例えば、1000人の身長の平均値が150cm、標準偏差が10cmの場合、140cm~160cmの範囲(標準偏差1つ分の範囲)の間に1000人中683人(68.3%)含まれているということを予想することができます。
この140cmは平均値150cmから標準偏差10cmを引くことで計算し、160cmは平均値150cmから標準偏差10cmを足すことで計算していますね。
【標準偏差の記号】『σ』と『s』の違い
標準偏差は「\({\sigma}\)(シグマ)」や「\(s\)」の記号で表されます。各記号は以下の場合で使用されることが多くなっています。
- \({\sigma}\):母集団の標準偏差
- \(s\):標本の標準偏差
例えば、生徒1000人のテストの点数について調査する場合を考えてみましょう。
1000人から50人を抜き取って調査する場合、この50人が標本となります。そのため、この50人のデータを用いて標準偏差を求める時には「\(s\)」の記号を用いることが多いです。
母集団とは調査対象全体のことです。そのため、1000人全てのデータを用いて、標準偏差を求める時には、「\({\sigma}\)」の記号を用いることが多いです。
まとめ
この記事では『標準偏差』について、以下の内容を説明しました。
- 標準偏差とは
- 標準偏差の求め方と例題
- 標準偏差がある理由
- 標準偏差の記号
- 『標準偏差』と『分散』の違い
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






