ダイオードの『電流二乗時間積I^2t』について！

この記事ではダイオードの絶対最大定格に記載されていることがある『電流二乗時間積\(I^2t\)』について説明しています。

ダイオードの『電流二乗時間積I²t』

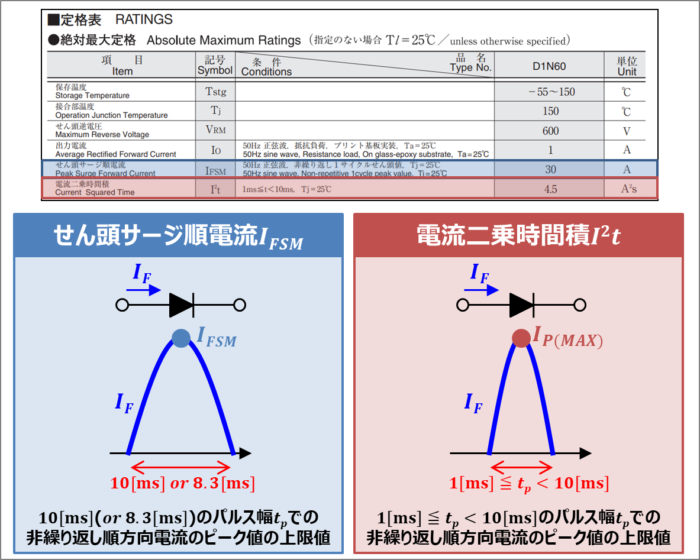
データシートの絶対最大定格に記載されていることがある『電流二乗時間積\(I^2t\)』は「\(1ms≦t_{p}＜10ms\)のパルス幅での非繰り返し順方向電流のピーク値の上限値\(I_{P(MAX)}\)」を算出するためのパラメータです。

データシートの絶対最大定格には『せん頭サージ順電流\(I_{FSM}\)』というパラメータがありますが、\(I_{FSM}\)は「\(50{\mathrm{Hz}}\)(もしくは\(60{\mathrm{Hz}}\))の正弦半波1サイクルの非繰り返し順方向電流のピーク値の上限値」となっています。\(50{\mathrm{Hz}}\)の場合は正弦半波のパルス幅\(t_p\)は\(10{\mathrm{[ms]}}\)、\(60{\mathrm{Hz}}\)の場合は正弦半波のパルス幅\(t_p\)は\(8.3{\mathrm{[ms]}}\)なので、\(I_{FSM}\)は「\(10{\mathrm{[ms]}}\)(もしくは\(8.3{\mathrm{[ms]}}\))のパルス幅での非繰り返し順方向電流のピーク値の上限値」ということになります。

『せん頭サージ順電流\(I_{FSM}\)』については下記の記事で詳しく説明していますのでご参考してください。

: 【ダイオードの絶対最大定格】『電流定格(IOやIFSMなど)』について！
続きを見る

しかし、実際の回路では、ダイオードに\(10{\mathrm{[ms]}}\)未満(もしくは\(8.3{\mathrm{[ms]}}\)未満)のパルス幅のサージ電流が流れることがあります。この場合、『せん頭サージ順電流\(I_{FSM}\)』は使用することができないため、『電流二乗時間積\(I^2t\)』を用いて、サージ電流のピーク値の上限値\(I_{P(MAX)}\)を求めます。

例えば、『電流二乗時間積\(I^2t\)』が\(4.5{\mathrm{[A^2s]}}\)であるダイオードにパルス幅\(t_p\)が\(2{\mathrm{[ms]}}\)の正弦半波が流れた場合、ピーク値の上限値\(I_{P(MAX)}\)は以下の値となります。『電流二乗時間積\(I^2t\)』の\(I\)は実効値なので、ピーク値の上限値\(I_{P(MAX)}\)を\(\sqrt{2}\)で割っています。

\begin{eqnarray}
I^2t&=&\left(\frac{I_{P(MAX)}}{\sqrt{2}}\right)^2×t_p=4.5\\
{\Leftrightarrow}I_{P(MAX)}&=&\sqrt{\displaystyle\frac{2I^2t}{t_p}}\\
&=&\sqrt{\displaystyle\frac{2×4.5}{2×10^{-3}}}\\
&=&67.0{\mathrm{[A]}}\tag{1}
\end{eqnarray}

補足

データシート上では『電流二乗時間積』ではなく『I²t限界値』と書かれていることがあります。
電流二乗時間積は英語のデータシートでは『I²t Limiting Value』や『Current Sequared Time』と書かれていることが多いです。
電流二乗時間積\(I^2t\)はヒューズでも規定されています。そのため、ヒューズの\(I^2t\)よりもダイオードの\(I^2t\)の方を大きくすることで、過大なサージ電流が流れた時、先にヒューズの方が切れて、ダイオードを保護することができます。

『電流二乗時間積I²t』と『せん頭サージ順電流I_FSM』の関係

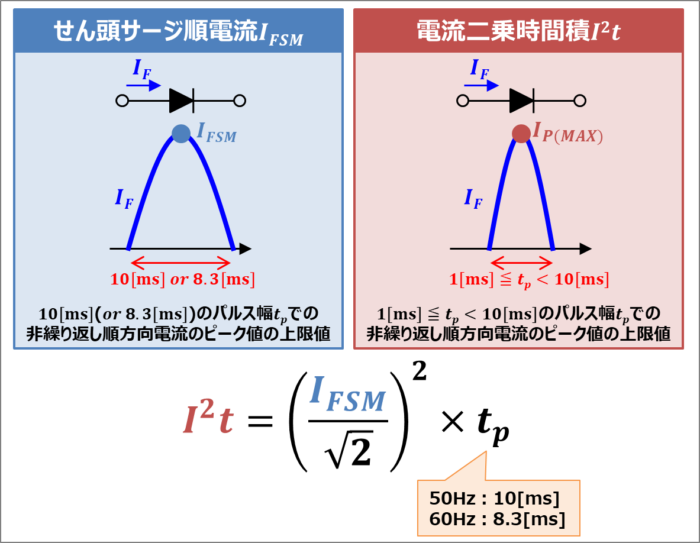
『電流二乗時間積\(I^2t\)』はデータシート上では記載されていないことがあります。この場合は『せん頭サージ順電流\(I_{FSM}\)』から『電流二乗時間積\(I^2t\)』を算出することができます。

『電流二乗時間積\(I^2t\)』と『せん頭サージ順電流\(I_{FSM}\)』には以下の関係式があります。

\begin{eqnarray}
I^2t&=&\left(\frac{I_{FSM}}{\sqrt{2}}\right)^2×t_p\tag{2}
\end{eqnarray}

\(I^2t\)の\(I\)は実効値なので、『せん頭サージ順電流\(I_{FSM}\)』を\(\sqrt{2}\)で割っています。また、\(50{\mathrm{Hz}}\)では\(t_p=10{\mathrm{[ms]}}\)、\(60{\mathrm{Hz}}\)では\(t_p=8.3{\mathrm{[ms]}}\)となります。

(2)式の関係は全てのデータシートに当てはまるわけではありませんので注意してください。

『電流二乗時間積I²t』の値

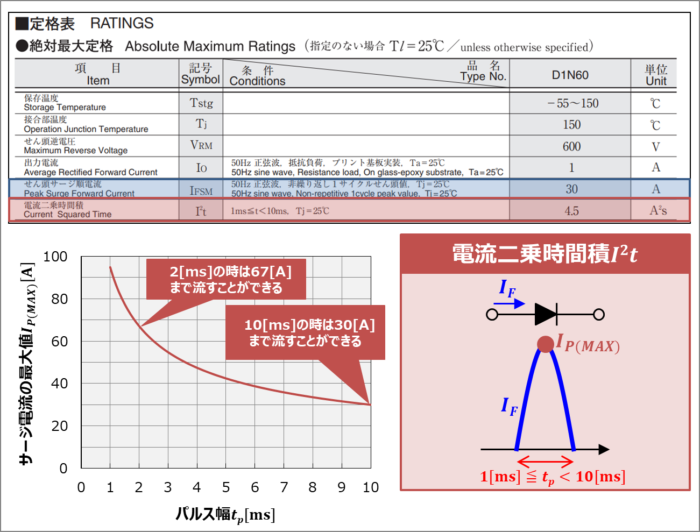
上図は新電元工業製ダイオードD1N60の絶対最大定格です。『電流二乗時間積\(I^2t\)』が\(4.5{\mathrm{[A^2s]}}\)であり、『せん頭サージ順電流\(I_{FSM}\)』が\(30{\mathrm{[A]}}\)となっています。

なお、(2)式に『せん頭サージ順電流\(I_{FSM}=30{\mathrm{[A]}}\)』と『\(t_p=10{\mathrm{[ms]}}\)』を代入しても、次式で表されるように、『電流二乗時間積\(I^2t\)』は\(4.5{\mathrm{[A^2s]}}\)になります。

\begin{eqnarray}
I^2t&=&\left(\frac{I_{FSM}}{\sqrt{2}}\right)^2×t_p\\
&=&\left(\frac{30{\mathrm{[A]}}}{\sqrt{2}}\right)^2×10{\mathrm{[ms]}}\\
&=&4.5{\mathrm{[A^2s]}}\tag{3}
\end{eqnarray}

また、『電流二乗時間積\(I^2t\)』を一定(\(4.5{\mathrm{[A^2s]}}\))として、「\(10{\mathrm{[ms]}}\)未満のパルス幅での非繰り返し順方向電流のピーク値」をプロットすると上図のようになります。パルス幅\(t_p\)が短いほど流せるピーク値の上限値\(I_{P(MAX)}\)が大きくなります。

『電流二乗時間積I²t』の使い方

一例として、上図のような正弦半波(ピーク値\(I_P=40{\mathrm{[A]}}\)、パルス幅\(t_p=2{\mathrm{[ms]}}\))がダイオードに流れた場合を考えてみましょう。

『電流二乗時間積\(I^2t\)』は以下の値となります。

\begin{eqnarray}
I^2t&=&\left(\frac{I_{P}}{\sqrt{2}}\right)^2×t_p\\
&=&\left(\frac{40{\mathrm{[A]}}}{\sqrt{2}}\right)^2×2{\mathrm{[ms]}}\\
&=&1.6{\mathrm{[A^2s]}}\tag{4}
\end{eqnarray}

そのため、『電流二乗時間積\(I^2t\)』が\(1.6{\mathrm{[A^2s]}}\)以上のダイオードを選定すれば、\(T_j=25{\mathrm{[℃]}}\)時での使用については問題ありません。

新電元工業製ダイオードD1N60は絶対最大定格に記載されている『電流二乗時間積\(I^2t\)』が\(4.5{\mathrm{[A^2s]}}\)なので、\(T_j=25{\mathrm{[℃]}}\)時では、使用することができるということになります。

『電流二乗時間積I²t』のディレーティング

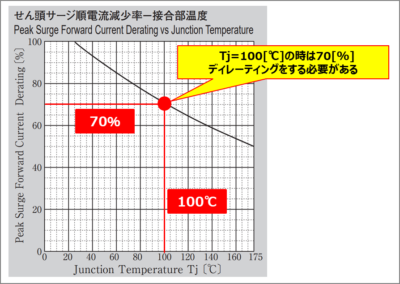
絶対最大定格に記載されている『電流二乗時間積\(I^2t\)』は\(T_j=25{\mathrm{[℃]}}\)時のみ保証しています。そのため、高温時には上図に示すような「せん頭サージ電流減少率―接合部温度T_j」を用いて、ディレーティングをする必要があります。上図の特性は新電元工業製ダイオードD6FEC15STのものです。

例えば、新電元工業製ダイオードD1N60の特性が上図と同じであるとすると、『\(T_j=100{\mathrm{[℃]}}\)時の電流二乗時間積\(I^2t\)』は『\(T_j=25{\mathrm{[℃]}}\)時の電流二乗時間積\(I^2t\)』に対して、70[%]のディレーティングが必要となるため、以下の値となり、『電流二乗時間積\(I^2t\)』が低下します。

\begin{eqnarray}
I^2t(T_j=100{\mathrm{[℃]}})&=&I^2t(T_j=25{\mathrm{[℃]}})×0.7\\
&=&4.5×0.7\\
&=&3.15{\mathrm{[A^2s]}}\tag{5}
\end{eqnarray}

そのため、\(T_j=100{\mathrm{[℃]}}\)時ではダイオードに流れるサージ電流の『電流二乗時間積\(I^2t\)』が\(3.15{\mathrm{[A^2s]}}\)以上の場合には使用することができなくなります。

補足

「せん頭サージ電流減少率―接合部温度T_j」はデータシート上に記載されていないことがほとんどです。