この記事では点電荷の電位について
- 点電荷の電位の公式
- 『電位の定義』と『公式の導出方法』
- 電位に関する簡単な例題
などを図を用いて分かりやすく説明しています。
点電荷の電位の公式
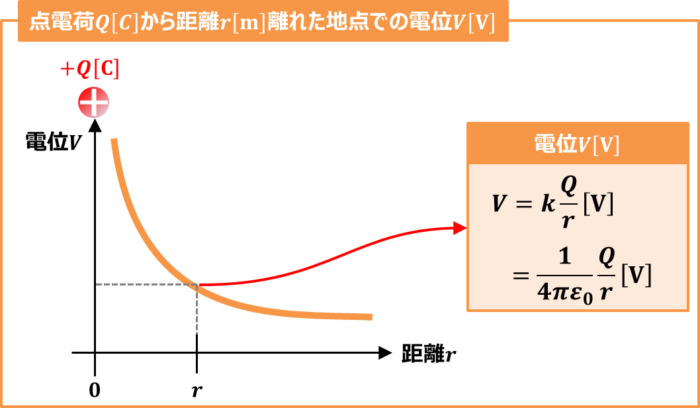
点電荷\(Q{\mathrm{[C]}}\)から距離\(r{\mathrm{[m]}}\)離れた地点での電位\(V{\mathrm{[V]}}\)は以下の式で表されます。
点電荷の電位の公式
\begin{eqnarray}
V&=&k\frac{Q}{r}\\
&=&\frac{1}{4{\pi}{\varepsilon}_0}\frac{Q}{r}{\mathrm{[V]}}
\end{eqnarray}
\(V\):電位\({\mathrm{[V]}}\)
\(Q\):点電荷の電気量\({\mathrm{[C]}}\)
\(r\):距離\({\mathrm{[m]}}\)
\({\varepsilon}_0\):真空の誘電率(\(8.854×10^{-12}{\mathrm{[F/m]}}\))
上図のグラフと式より、電位\(V{\mathrm{[V]}}\)は距離\(r{\mathrm{[m]}}\)に反比例することが分かります。
『電位の定義』と『公式の導出方法』
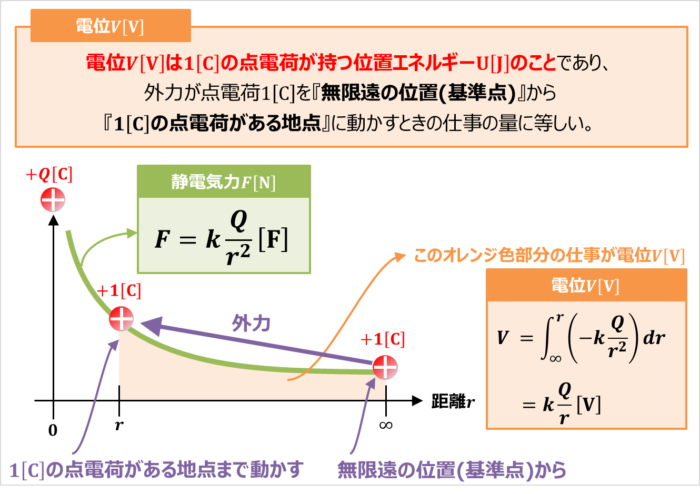
電位の定義
電位\(V{\mathrm{[V]}}\)は\(1{\mathrm{[C]}}\)の点電荷が持つ位置エネルギー\(U{\mathrm{[J]}}\)のことであり、外力が点電荷\(1{\mathrm{[C]}}\)を『無限遠の位置(基準点)』から『\(1{\mathrm{[C]}}\)の点電荷がある地点』に動かすときの仕事の量に等しくなります。
言い換えると、「\(1{\mathrm{[C]}}\)の電荷を\(1{\mathrm{[J]}}\)の仕事量である地点まで移動させると、\(1{\mathrm{[C]}}\)の点電荷がある地点の電位が\(1{\mathrm{[V]}}\)である」ということになります。
電位の定義は上に示したものとなります。仕事の量を計算することで、点電荷\(Q{\mathrm{[C]}}\)から距離\(r{\mathrm{[m]}}\)離れた地点での電位\(V=k\displaystyle\frac{Q}{r}{\mathrm{[V]}}\)を求めることができるので導出してみましょう。
電位の公式の導出方法
点電荷\(Q{\mathrm{[C]}}\)から距離\(r{\mathrm{[m]}}\)離れた地点に点電荷\(1{\mathrm{[C]}}\)がある場合、点電荷\(1{\mathrm{[C]}}\)が受ける静電気力\(F{\mathrm{[N]}}\)は次式で表されます。
\begin{eqnarray}
F=k\frac{Q}{r^2}{\mathrm{[N]}}\tag{1}
\end{eqnarray}
外力が点電荷\(1{\mathrm{[C]}}\)を『無限遠の位置(基準点)』から『距離\(r{\mathrm{[m]}}\)(点電荷がある地点)』に動かすときの仕事の量が、距離\(r{\mathrm{[m]}}\)の箇所における1[C]の点電荷が持つ位置エネルギー\(U{\mathrm{[J]}}\)(すなわち、電位\(V{\mathrm{[V]}}\))となります。
ただし、点電荷\(1{\mathrm{[C]}}\)が受ける静電気力\(F{\mathrm{[N]}}\)は距離が離れるにつれて小さくなります。そのため、電位\(V{\mathrm{[V]}}\)は以下のように積分計算で求めることが必要となります。
\begin{eqnarray}
V&=&{\displaystyle\int}_{\infty}^r \left(-k\frac{Q}{r^2}\right) dr\\
&=&\left[k\frac{Q}{r}\right]_{\infty}^r\\
&=&k\frac{Q}{r}{\mathrm{[V]}}\tag{2}
\end{eqnarray}
補足
(2)式の『\(-k\displaystyle\frac{Q}{r^2}\)』についているマイナスの符号は距離\(r{\mathrm{[m]}}\)の向きと外力の向きが逆なのでついています。
【電位の例題】電位は『スカラー量』なので重ね合わせる!
次に電位に関して簡単な例題を解いてみましょう。
例題
2つの点電荷\(Q{\mathrm{[C]}}\)が距離\(2r{\mathrm{[m]}}\)離れて置かれている時、距離\(r{\mathrm{[m]}}\)の地点における電位\(V{\mathrm{[V]}}\)を求めてみましょう。
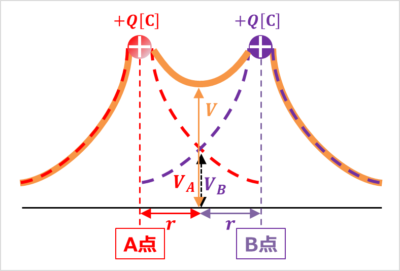
回答
点Aにある点電荷\(Q{\mathrm{[C]}}\)が距離\(r{\mathrm{[m]}}\)の地点における電位\(V_A{\mathrm{[V]}}\)は次式となります。
\begin{eqnarray}
V_A=k\frac{Q}{r}{\mathrm{[V]}}
\end{eqnarray}
同様に、点Bにある点電荷\(Q{\mathrm{[C]}}\)が距離\(r{\mathrm{[m]}}\)の地点における電位\(V_B{\mathrm{[V]}}\)は次式となります。
\begin{eqnarray}
V_B=k\frac{Q}{r}{\mathrm{[V]}}
\end{eqnarray}
電位は『スカラー量』なので電位\(V_A{\mathrm{[V]}}\)と電位\(V_B{\mathrm{[V]}}\)を足し合わせることで、距離\(r{\mathrm{[m]}}\)の地点における電位\(V{\mathrm{[V]}}\)を求めることができ、次式となります。
\begin{eqnarray}
V=V_A+V_B=k\frac{Q}{r}+k\frac{Q}{r}=k\frac{2Q}{r}{\mathrm{[V]}}
\end{eqnarray}
まとめ
この記事では点電荷の電位ついて、以下の内容を説明しました。
当記事のまとめ
- 点電荷の電位の公式
- 『電位の定義』と『公式の導出方法』
- 電位に関する簡単な例題
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






