【環状ソレノイドの自己インダクタンス】『公式』と『導出方法』について！

この記事では環状ソレノイドの自己インダクタンスについて

『環状ソレノイド』の自己インダクタンスの公式
『環状ソレノイド』の自己インダクタンスの導出方法
『環状ソレノイド』の自己インダクタンスの問題

などを図を用いて分かりやすく説明しています。

『環状ソレノイド』の自己インダクタンス

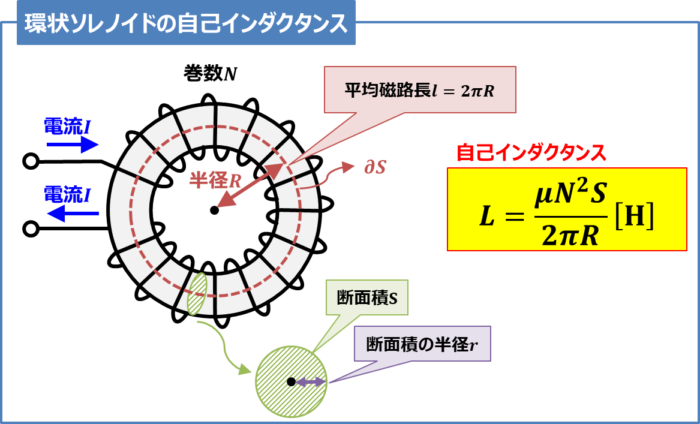
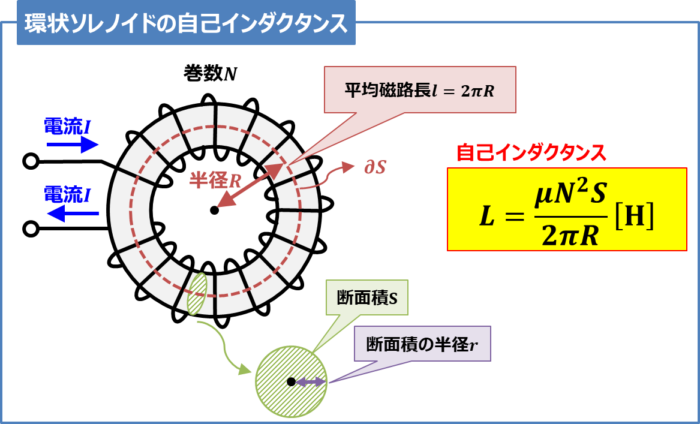
上図に示すような環状(ドーナツ状)の円筒に巻いたコイルを環状ソレノイドコイル(ドーナツ型コイル)といいます。

ここで、材料の透磁率\({\mu}{\mathrm{[H/m]}}\)、巻数\(N\)、平均半径\(R{\mathrm{[m]}}\)(平均磁路長\(l=2{\pi}R{\mathrm{[m]}}\))、断面積\(S{\mathrm{[m^2]}}\)の環状ソレノイドの自己インダクタンス\(L{\mathrm{[H]}}\)は次式となります。

『環状ソレノイド』の自己インダクタンス

\begin{eqnarray}
L=\frac{{\mu}N^2S}{2{\pi}R}{\mathrm{[H]}}
\end{eqnarray}

この記事では上式の導出方法について説明します。

『環状ソレノイド』の自己インダクタンスの導出方法

自己インダクタンス\(L\)は以下の流れによって導出することができます。

自己インダクタンスの導出の流れ

磁界の強さ\(H\)を求める
磁束密度\(B\)を求める
磁束\({\phi}\)を求める
磁束鎖交数\({\psi}\)を求める
自己インダクタンス\(L\)を求める

step
1磁界の強さ\(H\)を求める

アンペアの周回積分の法則より、以下の式が成り立ちます。

\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}=NI\tag{1}
\end{eqnarray}

巻数\(N\)なので、\({\partial}S\)に囲まれた面には『\(電流I×巻数N=NI\)』の電流が貫いています。そのため、(1)式の右辺が\(NI\)となります。

また、積分経路は円なので、\({\displaystyle\oint}_{{\partial}S}d{\vec{l}}=2{\pi}R\)が成り立ちます。ゆえに、(1)式を変形すると、磁界の強さ\(H\)は次式となります。

\begin{eqnarray}
{\displaystyle\oint}_{{\partial}S}{\vec{H}}{\;}{\cdot}{\;}d{\vec{l}}&=&NI\\
{\Leftrightarrow}2{\pi}R×H&=&NI\\
H&=&\frac{NI}{2{\pi}R}{\mathrm{[A/m]}}\tag{2}
\end{eqnarray}

step
2磁束密度\(B\)を求める

磁界の強さ\(H\)と磁束密度\(B\)と材料の透磁率\({\mu}\)の関係は『\(B={\mu}H\)』なので、磁束密度\(B\)は次式となります。

\begin{eqnarray}
B={\mu}H={\mu}×\frac{NI}{2{\pi}R}=\frac{{\mu}NI}{2{\pi}R}{\mathrm{[T]}}\tag{3}
\end{eqnarray}

step
3磁束\({\phi}\)を求める

磁束密度\(B\)と磁束\({\phi}\)の関係は『\({\phi}=BS\)』なので、ソレノイドの断面\(S\)と交わる磁束\({\phi}\)は次式となります。

\begin{eqnarray}
{\phi}=BS=\frac{{\mu}NI}{2{\pi}R}×S=\frac{{\mu}NIS}{2{\pi}R}{\mathrm{[wb]}}\tag{4}
\end{eqnarray}

step
4磁束鎖交数\({\psi}\)を求める

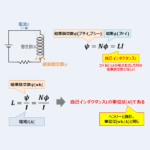
磁束\({\phi}\)と磁束鎖交数\({\psi}\)の関係は『\({\psi}=N{\phi}\)』なので、磁束鎖交数\({\psi}\)は次式となります。

\begin{eqnarray}
{\psi}=N{\phi}=N×\frac{{\mu}NIS}{2{\pi}R}=\frac{{\mu}N^2IS}{2{\pi}R}{\mathrm{[wb]}}\tag{5}
\end{eqnarray}

磁束鎖交数Ψと磁束Φの記号について

磁束鎖交数と磁束の記号は参考書やネットによって様々であり、磁束鎖交数の記号を\({\phi}\)(ファイ)や\({\psi}\)(プサイ,プシー)で表している場合もあります。

このサイトでは、

磁束鎖交数の記号：\({\psi}\)(プサイ,プシー)
磁束の記号；\({\phi}\)(ファイ)

で表示しています。

step
5自己インダクタンス\(L\)を求める

磁束鎖交数\({\psi}\)と自己インダクタンス\(L\)の関係は『\({\psi}=LI\)』なので、自己インダクタンス\(L\)は次式となります。

\begin{eqnarray}
L=\frac{{\psi}}{I}=\frac{\displaystyle\frac{{\mu}N^2IS}{2{\pi}R}}{I}=\frac{{\mu}N^2S}{2{\pi}R}{\mathrm{[H]}}\tag{6}
\end{eqnarray}

補足

磁路断面の半径を\(r{\mathrm{[m]}}\)とすれば、\(S={\pi}r^2\)より、自己インダクタンス\(L\)は次式となります。

\begin{eqnarray}
L=\frac{{\mu}N^2S}{2{\pi}R}=\frac{{\mu}N^2({\pi}r^2)}{2{\pi}R}=\frac{{\mu}N^2r^2}{2R}{\mathrm{[H]}}\tag{7}
\end{eqnarray}

上式も参考書やネットで見かけることがあります。

『環状ソレノイド』の自己インダクタンスに関する問題

問題文

巻数が\(2000\)回、断面積が\(6{\mathrm{[cm^2]}}\)、平均磁路長が\(40{\mathrm{[cm]}}\)の空心環状ソレノイドの自己インダクタンスを求めてみましょう。

回答

平均磁路長は『\(l=2{\pi}R=40{\mathrm{[cm]}}\)』、真空の透磁率は『\({\mu}_0=4{\pi}×10^{-7}{\mathrm{[H/m]}}\)』となるため、(6)式を用いると、自己インダクタンス\(L\)は以下の値となります。

\begin{eqnarray}
L&=&\frac{{\mu}_0N^2S}{2{\pi}R}\\
&=&\frac{4{\pi}×10^{-7}×2000^2×6×10^{-4}}{40×10^{-2}}\\
&{\approx}&7.53×10^{-3}{\mathrm{[H]}}
\end{eqnarray}