【ホール効果】『原理』や『半導体の判別』についてわかりやすく説明！

この記事ではホール効果について

ホール効果とは？
ホール効果の『原理』
ホール効果による『半導体の判別』
ホール電圧の大きさ
ホール係数とは？

などを図を用いて分かりやすく説明しています。

ホール効果とは

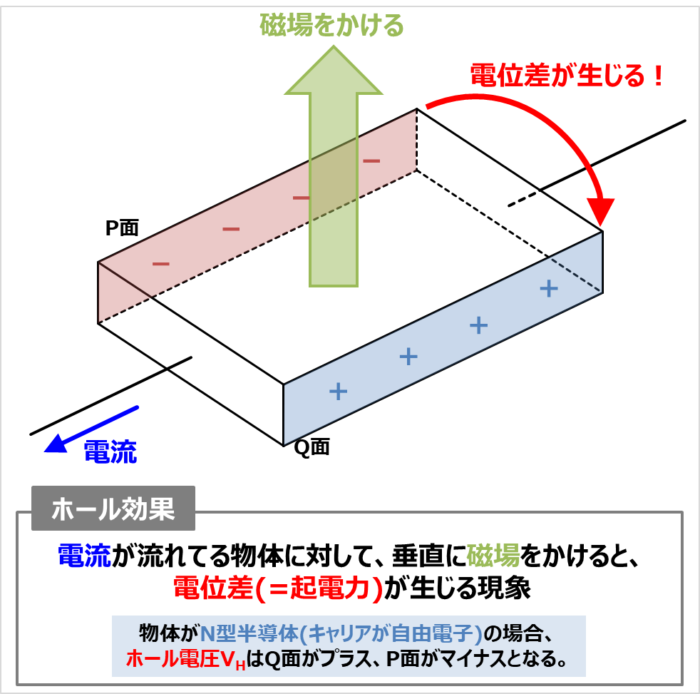
ホール効果とは、電流が流れている物体(半導体など)に対して、電流に垂直な磁場をかけると、電流と磁場の両方に垂直な向きに電位差(=起電力)が生じる現象です。

例えば、物体の幅を\(d{\mathrm{[m]}}\)、厚さを\(t{\mathrm{[m]}}\)、磁場の磁束密度を\(B{\mathrm{[T]}}\)、電流の大きさを\(I{\mathrm{[A]}}\)とすると、電位差\(V_{H}{\mathrm{[V]}}\)は次式となります。

\begin{eqnarray}
V_{H}=\frac{1}{en}\frac{IB}{t}=R_{H}\frac{IB}{t}{\mathrm{[V]}}\tag{1}
\end{eqnarray}

(1)式において、電位差\(V_H{\mathrm{[V]}}\)をホール電圧、\(R_H{\mathrm{[m^3/C]}}\)をホール係数と呼ばれています。なお、(1)式の\(e{\mathrm{[C]}}\)は『負電荷の自由電子1個の電気量の絶対値または正電荷の陽子1個の電気量』であり、電子素量と呼ばれるものです。\(n{\mathrm{[1/m^3]}}\)は自由電子の単位体積(1m³)あたりの個数(数密度と呼ばれる)となります。

また、物体がN型半導体かP型半導体かによって、ホール電圧\(V_H\)の向きが以下のように変わります(後ほど理由を説明します)。

N型半導体(キャリアが自由電子)の時

ホール電圧\(V_H\)はQ面がプラス、P面がマイナスとなります。

P型半導体(キャリアがホール)の時

ホール電圧\(V_H\)はQ面がマイナス、P面がプラスとなります。

補足

ホール効果は英語では「Hall Effect」と書きます。
1879年に米国の物理学者である「エドウィン・ホール(Edwin Herbert Hall)」によって発見されたため、ホール効果と呼ばれています。P型半導体のキャリアである「ホール(hole)」ではありませんので注意してください。
物体内のキャリア(自由電子やホール)がローレンツ力を受け、物体の端に移動することによって、電位差が生じています(後ほど原理を説明します)。

【ホール効果の原理】キャリアが自由電子の場合

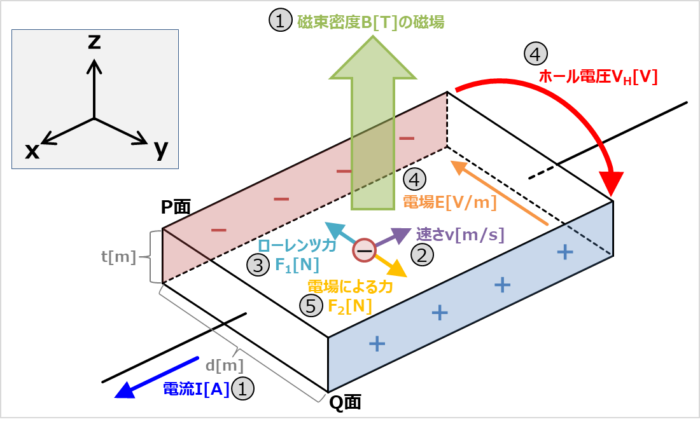
キャリアが自由電子(N型半導体)の時における、ホール効果の原理のポイントを以下に示します。

ホール効果の原理のポイント

物体に対して、電流を流し、磁場を掛ける
電流の向きと逆向きにキャリア(自由電子)が移動している
キャリア(自由電子)がローレンツ力を受ける
物体にホール電圧が生じる
ホール電圧による電場によってキャリア(自由電子)が力を受ける
電場による力とローレンツ力がつり合う

この各ポイントに沿って順番に説明します。

step
1物体に対して、電流を流し、磁場を掛ける

上図のような幅\(d{\mathrm{[m]}}\)、厚さ\(t{\mathrm{[m]}}\)の直方体の物体(キャリアが自由電子)において、電流\(I{\mathrm{[A]}}\)がx軸の正の向きに流れていて、磁束密度\(B{\mathrm{[T]}}\)の磁場がz軸の正の向きに掛かっているとします。

step
2電流の向きと逆向きにキャリア(自由電子)が移動している

この時、自由電子の進む向きは電流\(I{\mathrm{[A]}}\)と反対なので、x軸の負の方向に進んでいます(この時の速さを\(v{\mathrm{[m/s]}}\)とします)。

step
3キャリア(自由電子)がローレンツ力を受ける

この状態の場合、自由電子は磁場からy軸の負の方向にローレンツ力\(F_1{\mathrm{[N]}}\)を受けます。ローレンツ力\(F_1\)は自由電子1個の電気量を\(-e{\mathrm{[C]}}\)とすると、次式で表されます。

\begin{eqnarray}
F_1=evB{\mathrm{[N]}}\tag{2}
\end{eqnarray}

step
4物体にホール電圧が生じる

このローレンツ力\(F_1\)によりP面には自由電子が多く集まるため、P面は負(マイナス)に帯電します。一方、Q面は自由電子が不足するため、正(プラス)に帯電します。

『P面：マイナス、Q面：プラス』に帯電しているため、Q面がプラスでP面がマイナスとなる電位差(=起電力)\(V_H{\mathrm{[V]}}\)が生じます。そのため、電場\(E{\mathrm{[V/m]}}\)の向きはQ→Pとなります。

これがホール効果によって電位差が生じる原理となります。この電位差\(V_H\)をホール電圧といいます。

step
5ホール電圧による電場によってキャリア(自由電子)が力を受ける

また、自由電子は電場\(E\)による力\(F_2{\mathrm{[N]}}\)も受けます。電場\(E\)の向きはQ→Pとなるため、電場による力\(F_2\)はy軸の正の方向となります。つまり、ローレンツ力\(F_1\)と電場による力\(F_2\)の向きは逆となります。

また、電場による力\(F_2\)は次式で表されます。

\begin{eqnarray}
F_2=eE{\mathrm{[N]}}\tag{3}
\end{eqnarray}

step
6電場による力とローレンツ力がつり合う

ローレンツ力\(F_1\)により自由電子がP面に集まりますが、P面に集まる自由電子が増えるにつれて、電場\(E\)が大きくなります。すると、ローレンツ力\(F_1\)と電場による力\(F_2\)がつり合います。

力がつり合うと、自由電子は電流\(I\)の向きと逆の方向に真っ直ぐ進みます。この力がつり合っている時の電場\(E\)は、(2)式と(3)式を用いると、

\begin{eqnarray}
F_1&=&F_2\\
evB&=&eE\\
{\Leftrightarrow}E&=&vB\tag{4}
\end{eqnarray}

となります。ホール電圧\(V_H\)は電場\(E\)に幅\(d\)を掛けたものなので、

\begin{eqnarray}
V_H&=&Ed
&=&vBd\tag{5}
\end{eqnarray}

となります。

【ホール効果の原理】キャリアがホール(正孔)の場合

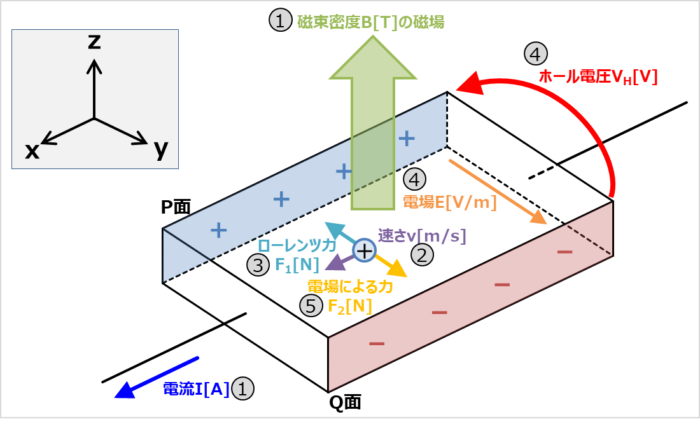
キャリアがホール(P型半導体)の時における、ホール効果の原理のポイントを以下に示します。キャリアが自由電子の場合と考え方は同じなので詳しい説明は割愛します。

ホール効果の原理のポイント

物体に対して、電流を流し、磁場を掛ける
電流の向きと逆向きにキャリア(ホール)が移動している
キャリア(ホール)がローレンツ力を受ける
物体にホール電圧が生じる
ホール電圧による電場によってキャリア(ホール)が力を受ける
電場による力とローレンツ力がつり合う

キャリアが自由電子の場合でもホールの場合でも、ローレンツ力\(F_1\)の向きは同じとなりますが、ホール電圧\(V_H\)の向きは違うので注意してください。

ホール効果で半導体の種類を判別

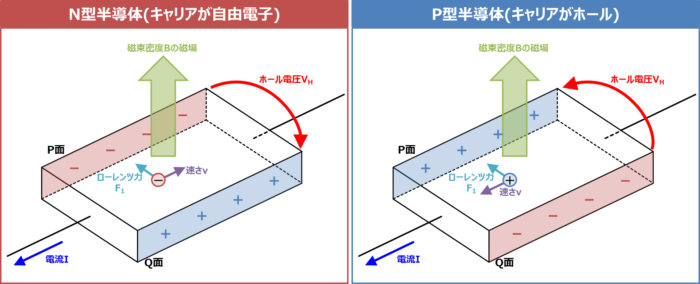
ホール効果を利用して、ホール電圧\(V_H\)の向きを測定すれば、キャリアが自由電子かホール(正孔)かを判別することができます。すなわち、半導体がN型半導体(キャリアが自由電子)かP型半導体(キャリアがホール)かを判別することができるということになります。

ホール電圧の大きさの導出

先ほどローレンツ力\(F_1\)と電場による力\(F_2\)がつり合っている時のホール電圧\(V_H\)の大きさは、

\begin{eqnarray}
V_H=vBd\tag{5}
\end{eqnarray}

であると説明しました。(5)式において、電流の大きさの式『\(I=envS\)』を用いると、物体中のキャリア(自由電子やホール)の数密度\(n{\mathrm{[1/m^3]}}\)を含んだ式に変形することができます。なお、数密度\(n{\mathrm{[1/m^3]}}\)とは、自由電子の単位体積(\(1m^3\))あたりの個数です。

『\(I=envS\)』の式において『\(S\)』は物体の表面積なので、『\(S=td{\mathrm{[m^2]}}\)』となります。ゆえに、電流\(I\)は次式となります。

\begin{eqnarray}
I=envS=envtd\tag{6}
\end{eqnarray}

上式を変形すると、次式となります。

\begin{eqnarray}
v=\frac{I}{entd}\tag{7}
\end{eqnarray}

(7)式を(5)式に代入すると、ホール電圧\(V_H\)の大きさは、次式となります。

\begin{eqnarray}
V_H=vBd=\frac{I}{entd}Bd=\frac{1}{en}\frac{IB}{t}{\mathrm{[V]}}\tag{8}
\end{eqnarray}

例えば、物体中のキャリア(自由電子やホール)の数密度\(n\)は(9)式において、ホール電圧\(V_H\)、磁束密度\(B\)、電流\(I\)、物体の厚さ\(t\)を測定して代入することで求めることができます。

今まで説明した内容をまとめると、ホール電圧\(V_H\)の大きさが分かると『物体中のキャリア(自由電子やホール)の数密度\(n\)』が分かり、ホール電圧\(V_H\)の向きが分かると『キャリアの種類』が分かるということになります。

そのため、ホール効果は、半導体の物性を調べる上で非常に重要となります。