『2端子法』と『4端子法』の違いを分かりやすく解説【抵抗計測】

この記事では『2端子法』と『4端子法』について

などを図を用いて分かりやすく説明しています。

『2端子法』と『4端子法』の違い

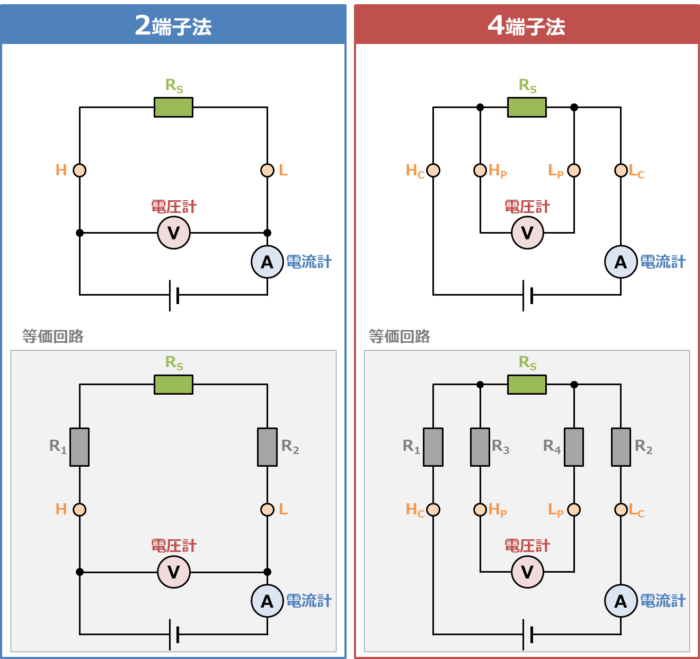
LCRメータなどで抵抗値を測定する方法には『2端子法』と『4端子法』があります。

上図の左側に2端子法の測定方法、右側に4端子法の測定方法を示しています。また、各測定方法の下段が等価回路になっています。

各等価回路において、抵抗\(R_S\)、\(R_1\)～\(R_4\)は下記を表しています。

後ほど詳しく説明しますが、先に2端子法と4端子法の要点を言うと、2端子法で抵抗\(R_S\)の抵抗値を測定する場合、抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)も一緒に測定してしまいます。

一方、4端子法で抵抗\(R_S\)の抵抗値を測定する場合、抵抗\(R_S\)の抵抗値のみを測定することができます。つまり、高精度の測定が4端子法では可能となります。

では実際に、2端子法と4端子法を用いて抵抗\(R_S\)を測定した時の誤差を求めています。

2端子法

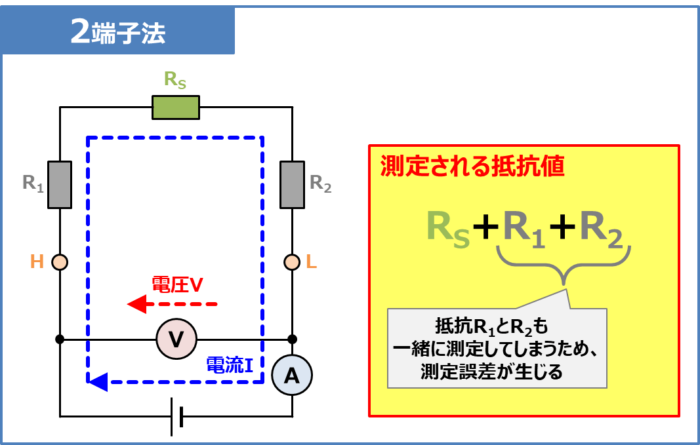
2端子法の場合、電流計で測定される電流\(I\)は\(R_1\)→\(R_S\)→\(R_2\)と流れます。そのため、電圧計で測定される電圧\(V\)は抵抗\(R_1\)・\(R_S\)・\(R_2\)にかかる電圧となり、次式で表されます。

\begin{eqnarray}
V=(R_1+R_S+R_2)I
\end{eqnarray}

以上より、抵抗\(R_S\)を2端子法で測定すると、測定される抵抗値\(R\)はオームの法則より次式となります。

\begin{eqnarray}
測定される抵抗値R&=&\frac{電圧計で測定される電圧V}{電流計で測定される電流I}\\
\\
&=&\frac{(R_1+R_S+R_2)I}{I}\\
\\
&=&R_1+R_S+R_2\\
\\
&=&R_S+R_1+R_2
\end{eqnarray}

上式より、2端子法の場合、抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)も一緒に測定してしまうため、それが測定誤差となってしまいます。これが2端子法のデメリットです。

『抵抗\(R_S\)の抵抗値』が大きく、抵抗\(R_1\)と\(R_2\)が無視できる場合には、2端子法でも測定誤差が小さくなるので問題はありません。

しかし、『抵抗\(R_S\)の抵抗値』が微小な場合には、2端子法での測定誤差が大きくなってしまいます。これは、抵抗\(R_1\)と\(R_2\)が抵抗\(R_S\)に対して相対的に大きくなるからです。

この問題を解決するための測定方法が4端子法になります。

4端子法

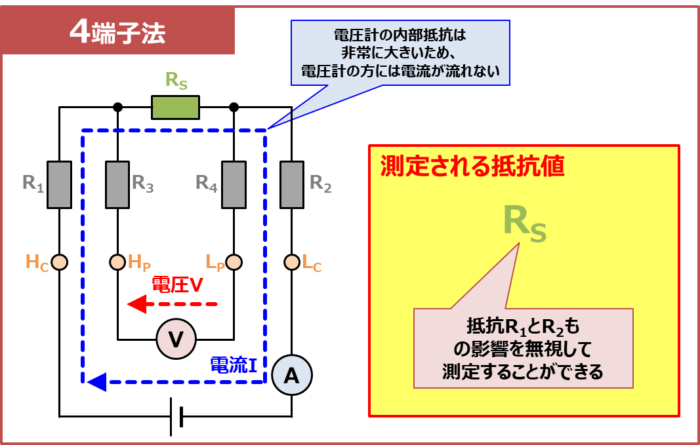
4端子法の場合、電圧計の内部抵抗は非常に大きいため、抵抗\(R_S\)に並列接続されている回路(電圧計・抵抗\(R_3\)・抵抗\(R_4\))にはほとんど電流が流れません。そこで、電流計で測定される電流\(I\)の全てが抵抗\(R_S\)に流れると仮定すると、電圧計で測定される電圧\(V\)は次式で表されます。

\begin{eqnarray}
V=R_SI
\end{eqnarray}

以上より、抵抗\(R_S\)を4端子法で測定すると、測定される抵抗値\(R\)はオームの法則より次式となります。

\begin{eqnarray}
測定される抵抗値R&=&\frac{電圧計で測定される電圧V}{電流計で測定される電流I}\\
\\
&=&\frac{R_SI}{I}\\
\\
&=&R_S
\end{eqnarray}

上式より、4端子法の場合、抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』、『リード線の配線抵抗』)の影響を無視して抵抗\(R_S\)を測定することができることが分かります。

このように、4端子法では『電流を流すリード線』と『電圧を測定するリード線』を分けることで、電圧計では抵抗\(R_S\)の電圧降下のみを測定することができます。そのため、4端子法では抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)による影響を受けず、『抵抗\(R_S\)の抵抗値』が微小な場合でも正確に測定することが可能となります。

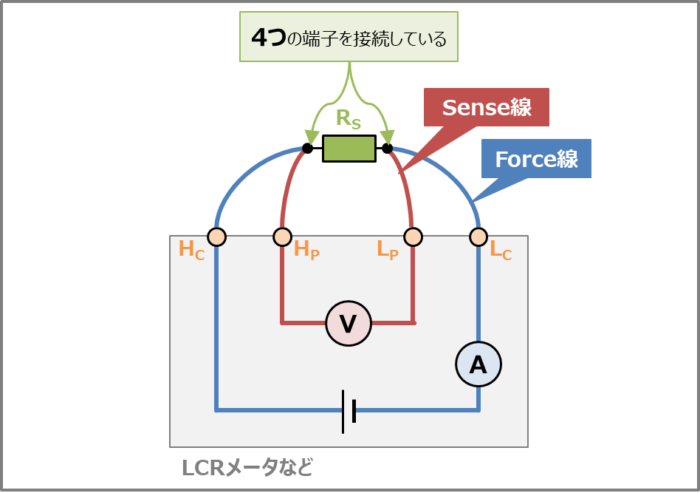
では次に、電圧計と電流計の内部抵抗を含んだ場合の誤差をキルヒホッフの法則を用いて計算してみます。

2端子法と4端子法での誤差をキルヒホッフの法則で計算する

2端子法と4端子法での誤差をキルヒホッフの法則を用いて計算します。ここでは、電圧計の内部抵抗\(R_V\)と電流計の内部抵抗\(R_A\)も考慮して計算します。

2端子法での誤差をキルヒホッフの法則で計算する

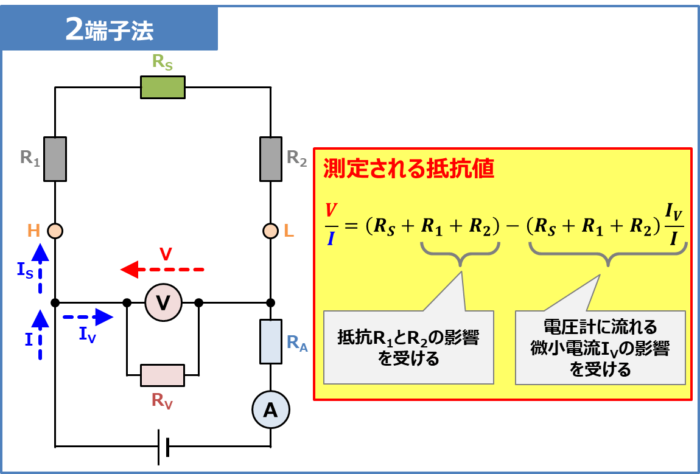
上図に2端子法の等価回路を示しています。抵抗\(R_S\)、\(R_1\)、\(R_2\)、\(R_V\)、\(R_A\)は下記を表しています。

電流計で測定される電流を\(I\)、電圧計に流れる電流を\(I_V\)、抵抗\(R_S\)に流れる電流を\(I_S\)とすると、キルヒホッフの電流則より次式が成り立ちます。

\begin{eqnarray}
I&=&I_V+I_S\\
\\
{\Leftrightarrow}I_S&=&I-I_V\tag{1-1}
\end{eqnarray}

電圧計で測定される電圧\(V\)はオームの法則より次式となります。

\begin{eqnarray}
V&=&R_VI_V\tag{1-2}
\end{eqnarray}

また、キルヒホッフの電圧則より次式が成り立ちます。

\begin{eqnarray}
V&=&R_VI_V\\
\\
&=&R_1I_S+R_SI_S+R_2I_S\\
\\
&=&(R_S+R_1+R_2)I_S\tag{1-3}
\end{eqnarray}

(1-1)式の\(I_S(=I-I_V)\)を(1-3)式に代入すると次式となります。

\begin{eqnarray}
V&=&(R_S+R_1+R_2)I_S\\
\\
&=&(R_S+R_1+R_2)(I-I_V)\tag{1-4}
\end{eqnarray}

(1-4)式の左辺と右辺を電流\(I\)で割ると次式となります。

\begin{eqnarray}
\frac{V}{I}&=&(R_S+R_1+R_2)(1-\frac{I_V}{I})\\
\\
&=&(R_S+R_1+R_2)-(R_S+R_1+R_2)\frac{I_V}{I}\tag{1-5}
\end{eqnarray}

以上より、測定対象の抵抗の抵抗値は\(R_S\)ですが、実際に測定される抵抗値はキルヒホッフの法則を用いると上式の値となります。

すなわち、抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)による影響と、電圧計に流れる微小電流\(I_V\)による影響を受けるため、本来の抵抗値\(R_S\)から誤差が生じます。

また、(1-3)式を\(I_S\)の式に直すと次式となります。

\begin{eqnarray}
V&=&R_VI_V\\
\\
&=&(R_S+R_1+R_2)I_S\\
\\
{\Leftrightarrow}I_S&=&\frac{R_V}{R_S+R_1+R_2}I_V\tag{1-6}
\end{eqnarray}

(1-6)式を(1-1)式に代入すると、電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)を求めることができ、次式となります。

\begin{eqnarray}
I&=&I_V+I_S\\
\\
&=&I_V+\frac{R_V}{R_S+R_1+R_2}I_V\\
\\
&=&\frac{R_S+R_1+R_2+R_V}{R_S+R_1+R_2}I_V\\
\\
{\Leftrightarrow}\frac{I_V}{I}&=&\frac{R_S+R_1+R_2}{R_S+R_1+R_2+R_V}\tag{1-7}
\end{eqnarray}

(1-7)式より電圧計の内部抵抗\(R_V\)が非常に大きいものを用いれば、電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)がゼロに近づくため、測定誤差が小さくなることが分かります。

しかし、2端子法では抵抗\(R_1\)と\(R_2\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)による影響が無くなることはありません。なぜなら、(1-5)式を見ると、抵抗\(R_1\)と\(R_2\)に電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)が掛けれれていない箇所があるからです。

4端子法での誤差をキルヒホッフの法則で計算する

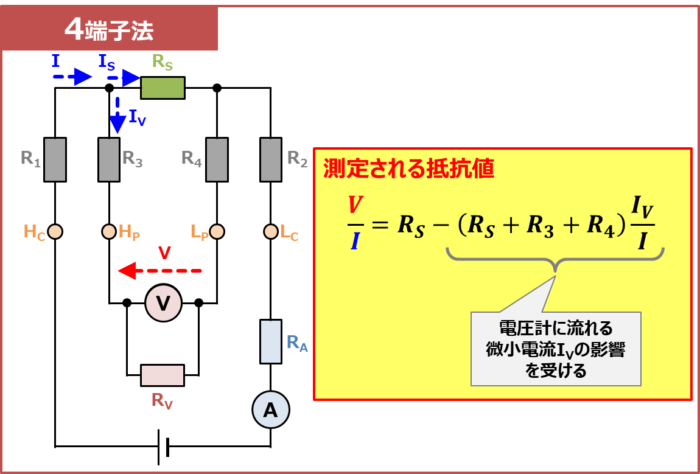
上図に4端子法の等価回路を示しています。抵抗\(R_S\)、\(R_1\)～\(R_4\)、\(R_V\)、\(R_A\)は下記を示しています。

電流計で測定される電流を\(I\)、電圧計に流れる電流を\(I_V\)、抵抗\(R_S\)に流れる電流を\(I_S\)とすると、キルヒホッフの電流則より次式が成り立ちます。

\begin{eqnarray}
I&=&I_V+I_S\tag{2-1}
\end{eqnarray}

電圧計で測定される電圧\(V\)はオームの法則より次式となります。

\begin{eqnarray}
V&=&R_VI_V\tag{2-2}
\end{eqnarray}

また、キルヒホッフの電圧則より次式が成り立ちます。

\begin{eqnarray}
R_SI_S&=&R_3I_V+R_VI_V+R_4I_V\\
\\
&=&R_3I_V+V+R_4I_V\\
\\
{\Leftrightarrow}V&=&R_SI_S-(R_3I_V+R_4I_V)\\
\\
&=&R_SI_S-(R_3+R_4)I_V\tag{2-3}
\end{eqnarray}

(2-1)式の\(I_S(=I-I_V)\)を(2-3)式に代入すると次式となります。

\begin{eqnarray}
R_SI_S&=&R_SI_S-(R_3+R_4)I_V\\
\\
&=&R_S(I-I_V)-(R_3+R_4)I_V\\
\\
&=&R_SI-(R_S+R_3+R_4)I_V\tag{2-4}
\end{eqnarray}

(2-4)式の左辺と右辺を電流\(I\)で割ると次式となります。

\begin{eqnarray}
\frac{V}{I}&=&R_S-(R_S+R_3+R_4)\frac{I_V}{I}\tag{2-5}
\end{eqnarray}

以上より、測定対象の抵抗の抵抗値は\(R_S\)ですが、実際に測定される抵抗値はキルヒホッフの法則を用いると上式の値となります。

すなわち、抵抗\(R_3\)と\(R_4\)(『測定対象の抵抗とリード線との接触抵抗』や『リード線の配線抵抗』)による影響と、電圧計に流れる微小電流\(I_V\)による影響を受けるため、本来の抵抗値\(R_S\)からの誤差が生じますが、電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)は非常に小さい値のため、誤差は小さくなります。

また、(2-3)式を\(I_S\)の式に直すと次式となります。

\begin{eqnarray}
R_SI_S&=&R_3I_V+R_VI_V+R_4I_V\\
\\
{\Leftrightarrow}I_S&=&\frac{R_3+R_4+R_V}{R_S}I_V\tag{2-6}
\end{eqnarray}

(2-6)式を(2-1)式に代入すると、電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)を求めることができ、次式となります。

\begin{eqnarray}
I&=&I_V+I_S\\
\\
&=&I_V+\frac{R_3+R_4+R_V}{R_S}I_V\\
\\
&=&\frac{R_S+R_3+R_4+R_V}{R_S}I_V\\
\\
{\Leftrightarrow}\frac{I_V}{I}&=&\frac{R_S}{R_S+R_3+R_4+R_V}\tag{2-7}
\end{eqnarray}

(2-7)式より電圧計の内部抵抗\(R_V\)が非常に大きいものを用いれば、電圧計に流れる電流\(I_V\)の割合\(\left(\displaystyle\frac{I_V}{I}\right)\)がゼロに近づくため、測定誤差が小さくなることが分かります。

まとめ

この記事では『2端子法』と『4端子法』について、以下の内容を説明しました。

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。

全記事一覧

また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。