『ボルテージフォロワ』を分かりやすく解説！【オペアンプ】

この記事ではボルテージフォロワについて

ボルテージフォロワの特徴
ボルテージフォロワと非反転増幅回路の関係
ボルテージフォロワの用途

を図を用いて説明しています。

ボルテージフォロワの特徴

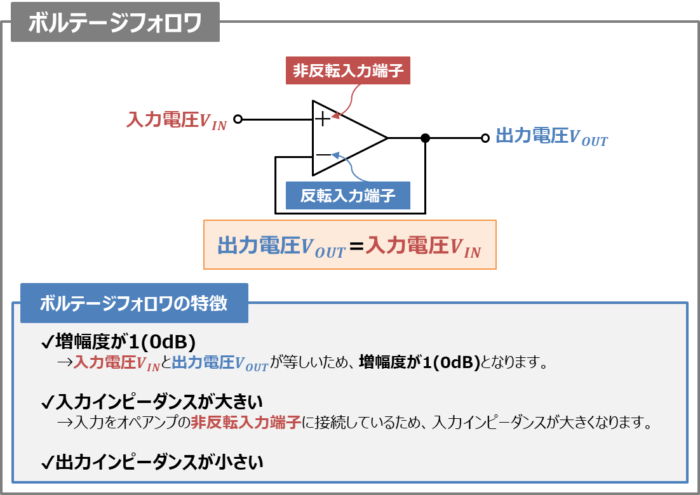
ボルテージフォロワはオペアンプを用いた回路の1つです。

ボルテージフォロワの回路図は上図のようになっています。入力を非反転入力端子(オペアンプの「＋」の箇所)に接続し、出力を反転入力端子(オペアンプの「－」の箇所)に接続したとてもシンプルな回路となっています。

動作もシンプルです。入力をそのまま出力しています。すなわち、ボルテージフォロワの入力電圧を\(V_{IN}\)、出力電圧を\(V_{OUT}\)としたとき、入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の関係式は以下のようになります。

ボルテージフォロワの式

\begin{eqnarray}
V_{OUT}=V_{IN}
\end{eqnarray}

また、ボルテージフォロワの特徴は下記となっています。

ボルテージフォロワの特徴

増幅度が1(0dB)

→入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)が等しいため、増幅度が1(0dB)となります。

入力インピーダンスが大きい

→入力をオペアンプの非反転入力端子(オペアンプの「＋」の箇所)に接続しているため、入力インピーダンスが大きくなります。

出力インピーダンスが小さい

ボルテージフォロワと非反転増幅回路の関係

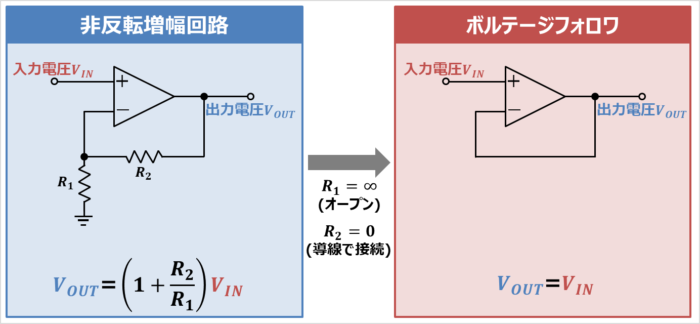
ボルテージフォロワは非反転増幅回路の一種です。具体的には、増幅度が1の非反転増幅回路となります。

非反転増幅回路の『入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の関係式』は以下の式となっています。

ボルテージフォロワの式

\begin{eqnarray}
V_{OUT}=\left(1+\frac{R_2}{R_1}\right)V_{IN}
\end{eqnarray}

上式において、『\(R_1=∞\)』、『\(R_2=0\)』となると、入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)が等しくなり、増幅度が1となります。『\(R_1=∞\)』とするためには\(R_1\)をオープン(無接続)、『\(R_2=0\)』とするためには\(R_2\)をショート(導線で接続)させます。すると、回路図もボルテージフォロワと同じになります。

オペアンプの非反転入力端子(オペアンプの「＋」の箇所)と反転入力端子(オペアンプの「－」の箇所)の電圧はイマジナリショート(仮想短絡)より、等しくなります。ボルテージフォロワは非反転入力端子は入力に、反転入力端子は出力に接続されているため、入力と出力が等しくなります。

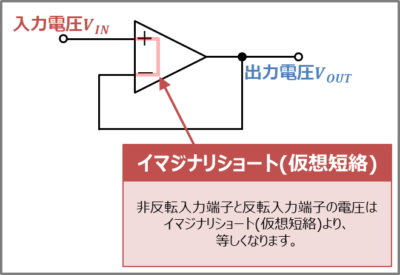
【補足】イマジナリショート(仮想短絡)とは？

オペアンプは、非反転入力端子(オペアンプの「＋」の箇所)と反転入力端子(オペアンプの「－」の箇所)の電位差が0Vになるように動作を行っています。そのため、非反転入力端子と反転増幅端子の電圧は等しくなります。このように、短絡(ショート)していないのに、常に2つの入力端子の電圧が同じになることからイマジナリショート(仮想短絡)と呼ばれています。イマジナリショート(仮想短絡)は、バーチャルショート、仮想接地とも呼ばれています。後日、イマジナリショートについて詳しく記事を書きます。

ボルテージフォロワの用途

ボルテージフォロワは入力と出力が等しいので、増幅度が1(=0dB)の回路となります。

『入力をそのまま出力する回路に何の意味があるの？どこに使われるの？』と思う方が多いと思います。

このボルテージフォロワは増幅用途ではなく、『インピーダンス変換』と『回路の分離』に用いられています。

次に各用途について詳しく説明していきます。

インピーダンス変換

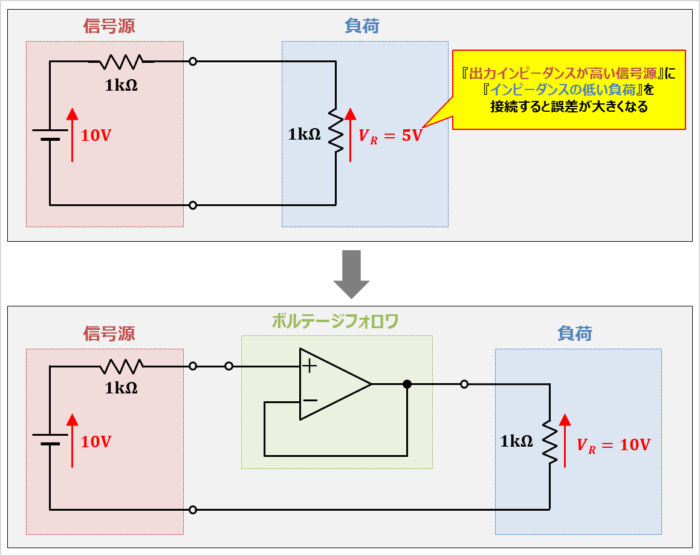
上図に示すように、出力インピーダンスが1kΩで10Vの電圧を出力している信号源があるとします。この信号源に1kΩの負荷を接続すると、負荷にかかる電圧\(V_R\)は

\begin{eqnarray}
V_R=\frac{1{\mathrm{kΩ}}}{1{\mathrm{kΩ}}+1{\mathrm{kΩ}}}×10{\mathrm{V}}=5{\mathrm{V}}
\end{eqnarray}

となり、10Vの電圧を負荷に印加することができません。この場合、負荷に10Vを印加したいのに5Vしか印加されていないため、50%程度の誤差が生じています。このように、『出力インピーダンスが高い信号源』に『インピーダンスの低い負荷』を接続すると誤差が大きくなります。

言い換えると、信号源の電圧を正しく負荷に印加するには、『信号源の出力インピーダンス』より『負荷のインピーダンス』の方が十分高いことが必要となります。

このような場合にボルテージフォロワを用いると解決することができます。

ボルテージフォロワは入力インピーダンスが非常に高い(100MΩ前後)という特徴を持っています。そのため、負荷の前段にボルテージフォロワを接続することで、負荷側のインピーダンスの影響を無視することができます。

このような使い方を一般にバッファを呼びます。

信号源に電流が流れることによって信号源の出力インピーダンスによる電圧降下が起こってしまいます。そのため、ボルテージフォロワを接続して、信号源に流れる電流をほぼゼロにし、信号源の出力インピーダンスによる電圧降下を生じさせないようにしているのです。

回路の分離

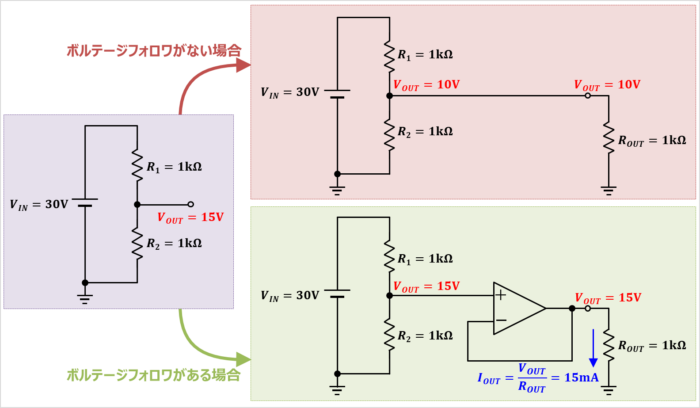
上図に示すように、入力電圧\(V_{IN}=30{\mathrm{V}}\)の直流電圧源を1kΩの2つの抵抗(\(R_1\),\(R_2\))で分圧している回路があるとします。この時、2つの抵抗の間を出力電圧\(V_{OUT}\)とした時、出力電圧\(V_{OUT}\)は以下の値となります。

\begin{eqnarray}
V_{OUT}=\frac{R_2}{R_1+R_2}×V_{IN}=\frac{1{\mathrm{kΩ}}}{1{\mathrm{kΩ}}+1{\mathrm{kΩ}}}×30{\mathrm{V}}=15{\mathrm{V}}
\end{eqnarray}

この出力に負荷をつなげたときにどのようになるでしょうか。例えば、1kΩの負荷\(R_{OUT}\)がつながると、下側の合成抵抗\(R_3\)は以下の値となります。

\begin{eqnarray}
R_3=\frac{1}{\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_{OUT}}}=\frac{1}{\displaystyle\frac{1}{1{\mathrm{kΩ}}}+\displaystyle\frac{1}{1{\mathrm{kΩ}}}}=0.5{\mathrm{kΩ}}
\end{eqnarray}

その結果、出力電圧\(V_{OUT}\)は以下の値となり、負荷\(R_{OUT}\)が接続されることによって出力電圧が変化してしまいます。

\begin{eqnarray}
V_{OUT}=\frac{R_3}{R_1+R_3}×V_{IN}=\frac{0.5{\mathrm{kΩ}}}{1{\mathrm{kΩ}}+0.5{\mathrm{kΩ}}}×30{\mathrm{V}}=10{\mathrm{V}}
\end{eqnarray}

このような場合に負荷の前段にボルテージフォロワを用いると、出力電圧の変化を解決することができます。

ボルテージフォロワは入力インピーダンスが非常に高い(100MΩ前後)という特徴を持っています。そのため、負荷の前段にボルテージフォロワを接続することで、分圧回路に影響を与えなくなります。その結果、出力電圧\(V_{OUT}\)は\(V_{OUT}=15{\mathrm{V}}\)となり、負荷の抵抗値の影響を無視することができます。

なお、負荷には以下の負荷電流が流れます。

\begin{eqnarray}
I_{OUT}=\frac{V_{OUT}}{R_{OUT}}=\frac{15{\mathrm{V}}}{1{\mathrm{kΩ}}}=15{\mathrm{mA}}
\end{eqnarray}

また、直流電圧源の入力電圧\(V_{IN}\)が変化すると、出力電圧\(V_{OUT}\)が変化しますが、負荷\(R_{OUT}\)が変化しても、出力電圧\(V_{OUT}\)は変化しません。

すなわち、電圧源と負荷の間にボルテージフォロワを接続すると、電圧源の変化は負荷に伝わりますが、負荷の変化は電圧源に影響を及ぼしません。これが、回路の分離となります。