この記事では平行往復導線の自己インダクタンスについて
- 『平行往復導線』の自己インダクタンスの公式
- 『平行往復導線』の自己インダクタンスの導出方法
などを図を用いて分かりやすく説明しています。
『平行往復導線』の自己インダクタンス
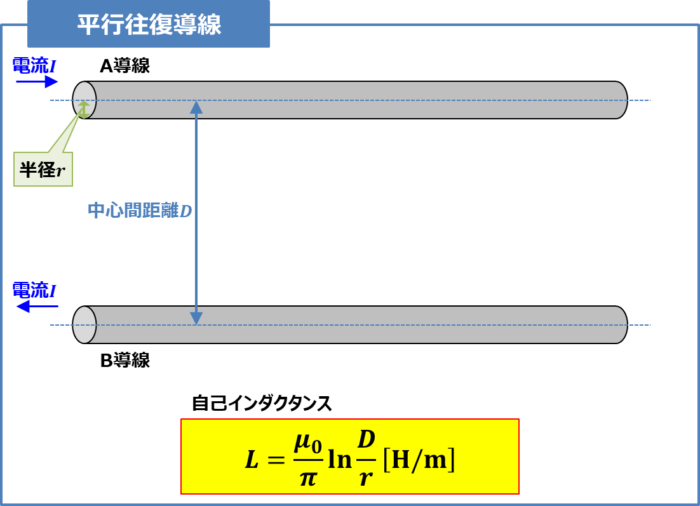
半径\(r{\mathrm{[m]}}\)の非常に長い2本の直流導体が中心間距離\(D{\mathrm{[m]}}\)離れて置かれており、往復導線となっている場合、導線の単位長さあたりの自己インダクタンス\(L{\mathrm{[H/m]}}\)は次式となります。
『平行往復導線』の自己インダクタンス
\begin{eqnarray}
L=\frac{{\mu}_0}{{\pi}}{\ln}\frac{D}{r}{\mathrm{[H/m]}}
\end{eqnarray}
この記事では上式の導出方法について説明します。
『平行往復導線』の自己インダクタンスの導出方法
自己インダクタンス\(L\)は以下の流れによって導出することができます。
自己インダクタンスの導出の流れ
- 磁界の強さ\(H\)を求める
- 磁束密度\(B\)を求める
- 磁束\({\phi}\)を求める
- 磁束鎖交数\({\psi}\)を求める
- 自己インダクタンス\(L\)を求める
step
1磁界の強さ\(H\)を求める
往復導線の単位長さあたりの自己インダクタンス\(L\)は『単位長さあたりの両導線間の面積を通る磁束鎖交数\({\psi}\)』を計算することによって求めることができます。
磁束鎖交数\({\psi}\)を求めるためには、『磁界の強さ\(H\)→磁束密度\(B\)→磁束\({\phi}\)』を求める必要があるので、順番に導出していきます。
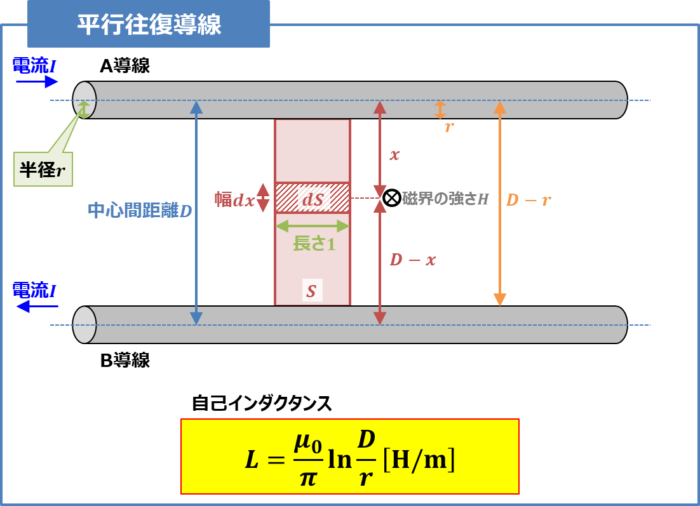
上図において、上側の導線をA導線、下側の導線をB導線とすると、A導線の中心から距離\(x{\mathrm{[m]}}\)離れた点に生じる磁界の強さ\(H\)は次式となります。
\begin{eqnarray}
H=\frac{I}{2{\pi}x}+\frac{I}{2{\pi}(D-x)}{\mathrm{[A/m]}}\tag{1}
\end{eqnarray}
(1)式において、第1項の\(\displaystyle\frac{I}{2{\pi}x}\)はA導線が作る磁界の強さ、第2項の\(\displaystyle\frac{I}{2{\pi}(D-x)}\)はB導線が作る磁界の強さとなります。
なお、磁界の向きはA導線とB導線を含む平面に垂直となります。
step
2磁束密度\(B\)を求める
磁界の強さ\(H\)と磁束密度\(B\)と真空の透磁率\({\mu}_0\)の関係は『\(B={\mu}_0H\)』なので、磁束密度\(B\)は次式となります。
\begin{eqnarray}
B&=&{\mu}_0H\\
&=&{\mu}_0×\left(\frac{I}{2{\pi}x}+\frac{I}{2{\pi}(D-x)}\right)\\
&=&\frac{{\mu}_0I}{2{\pi}x}+\frac{{\mu}_0I}{2{\pi}(D-x)}{\mathrm{[T]}}\tag{2}
\end{eqnarray}
step
3磁束\({\phi}\)を求める
A導線から距離\(x{\mathrm{[m]}}\)離れた近傍において、幅\(dx{\mathrm{[m]}}\)、長さ\(1{\mathrm{[m]}}\)の微小面積\(dS\)を考えると、その微小面積\(dS\)を通る磁束\(d{\phi}\)は次式となります。
\begin{eqnarray}
d{\phi}&=&B×dS\\
&=&\left(\frac{{\mu}_0I}{2{\pi}x}+\frac{{\mu}_0I}{2{\pi}(D-x)}\right)×(1×dx)\\
&=&\frac{{\mu}_0I}{2{\pi}}\left(\frac{1}{x}+\frac{1}{D-x}\right)dx\tag{3}
\end{eqnarray}
長さ\(1{\mathrm{[m]}}\)、両導線間の面積\(S\)を通る磁束\({\phi}\)は『\(x\)を\(r\)から\(D-r\)まで積分する』ことで求めることができ、次式となります。
\begin{eqnarray}
{\phi}&=&{\displaystyle\int}_r^{D-r}d{\phi}\\
&=&{\displaystyle\int}_r^{D-r}\frac{{\mu}_0I}{2{\pi}}\left(\frac{1}{x}+\frac{1}{D-x}\right)dx\\
&=&\frac{{\mu}_0I}{2{\pi}}{\displaystyle\int}_r^{D-r}\left(\frac{1}{x}+\frac{1}{D-x}\right)dx\\
&=&\frac{{\mu}_0I}{2{\pi}}\left[{\ln}x-{\ln}(D-x)\right]_r^{D-r}\\
&=&\frac{{\mu}_0I}{{\pi}}{\ln}\frac{D-r}{r}{\mathrm{[wb]}}\tag{4}
\end{eqnarray}
step
4磁束鎖交数\({\psi}\)を求める
磁束\({\phi}\)と磁束鎖交数\({\psi}\)の関係は『\({\psi}=N{\phi}\)』となります。今回、巻数\(N\)は\(1\)なので、磁束鎖交数\({\psi}\)は次式となります。
\begin{eqnarray}
{\psi}&=&N{\phi}\\
&=&1×{\phi}\\
&=&\frac{{\mu}_0I}{{\pi}}{\ln}\frac{D-r}{r}{\mathrm{[wb]}}\tag{5}
\end{eqnarray}
磁束鎖交数Ψと磁束Φの記号について
磁束鎖交数と磁束の記号は参考書やネットによって様々であり、磁束鎖交数の記号を\({\phi}\)(ファイ)や\({\psi}\)(プサイ,プシー)で表している場合もあります。
このサイトでは、
- 磁束鎖交数の記号:\({\psi}\)(プサイ,プシー)
- 磁束の記号;\({\phi}\)(ファイ)
で表示しています。
step
5自己インダクタンス\(L\)を求める
磁束鎖交数\({\psi}\)と自己インダクタンス\(L\)の関係は『\({\psi}=LI\)』なので、単位長さあたりの自己インダクタンス\(L\)は次式となります。
\begin{eqnarray}
L&=&\frac{{\psi}}{I}\\
&=&\frac{{\mu}_0}{{\pi}}{\ln}\frac{D-r}{r}\\
&=&4{\;}{\ln}\frac{D-r}{r}×10^{-7}{\mathrm{[H/m]}}\tag{6}
\end{eqnarray}
したがって、長さ\(l{\mathrm{[m]}}\)の自己インダクタンス\(L_l\)は次式となります。
\begin{eqnarray}
L_l&=&L×l\\
&=&\frac{{\mu}_0l}{{\pi}}{\ln}\frac{D-r}{r}\\
&=&4l{\;}{\ln}\frac{D-r}{r}×10^{-7}{\mathrm{[H]}}\tag{7}
\end{eqnarray}
ここで、中心間距離\(D{\mathrm{[m]}}\)が2本の直流導体の半径\(r{\mathrm{[m]}}\)より非常に大きいとすると(\(D{≫}r\))、(6)式と(7)式は次式となります。
- 単位長さあたりの自己インダクタンス\(L{\mathrm{[H/m]}}\)
- 長さ\(l{\mathrm{[m]}}\)の自己インダクタンス\(L_l{\mathrm{[H]}}\)
\begin{eqnarray}
L&=&\frac{{\mu}_0}{{\pi}}{\ln}\frac{D}{r}\\
&=&4{\;}{\ln}\frac{D}{r}×10^{-7}{\mathrm{[H/m]}}
\end{eqnarray}
\begin{eqnarray}
L_l&=&\frac{{\mu}_0l}{{\pi}}{\ln}\frac{D}{r}\\
&=&4l{\;}{\ln}\frac{D}{r}×10^{-7}{\mathrm{[H]}}
\end{eqnarray}
あわせて読みたい
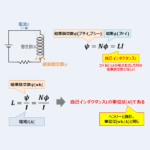
『\({\psi}=LI\)』の関係と自己インダクタンスについては以下の記事で説明していますので、参考にしてください。
-

【自己インダクタンスのまとめ】『単位』や『問題』などを解説!
続きを見る
まとめ
この記事では平行往復導線の自己インダクタンスついて、以下の内容を説明しました。
当記事のまとめ
- 『平行往復導線』の自己インダクタンスの公式
- 『平行往復導線』の自己インダクタンスの導出方法
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。