電気回路の勉強をしていると『開放』と『短絡』という言葉が出てきます。
普段は当たり前のように使用している言葉ですが、電気回路の勉強を初めたばかりの方は『開放』と『短絡』について分からないと思います。
この記事では『開放』と『短絡』の違いについて図や式を用いて分かりやすく説明します。お役に立てれば幸いです。
『開放』と『短絡』の違い
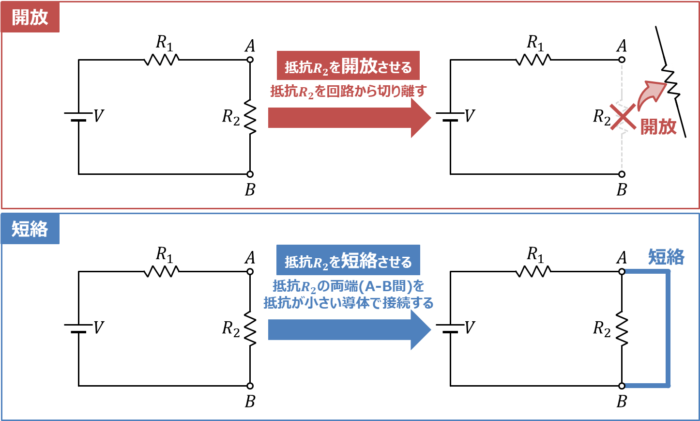
後ほど詳しく説明しますが、最初に『開放』と『短絡』の違いを説明します。
開放とは『回路の一部が途切れている状態』のことを指します。
上図の回路の場合、「抵抗R2を開放させる」ということは「抵抗R2を回路から切り離す」ということを意味しています。抵抗R2を切り離すと、回路が途切れた状態となります。
短絡とは『回路において電位差のある2点間を抵抗が小さい導体(電線など)で接続している状態』のことを指します。
上図の回路の場合、「抵抗R2を短絡させる」ということは「抵抗R2の両端(A-B間)を抵抗が小さい導体(電線など)で接続する」ということを意味しています。
では、次に各用語について順番に詳しく説明していきます。
開放とは
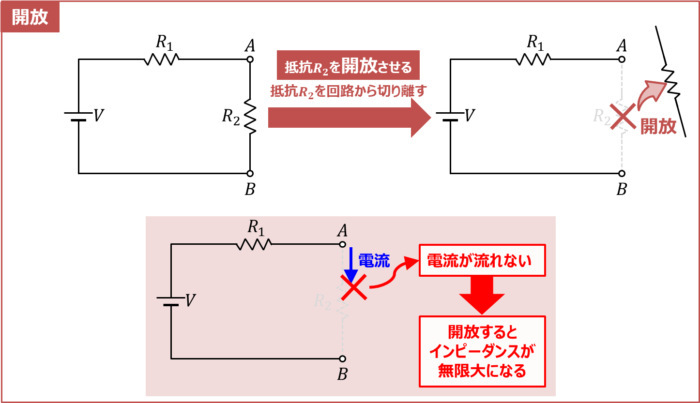
開放とは回路の一部が途切れている状態のことを指します。開放は『オープン』とも呼ばれています。
上図に電圧源V、抵抗R1、抵抗R2で構成されたシンプルな回路を示しています。この回路において、抵抗R2を開放させる」ということは「抵抗R2を回路から切り離す」ということを意味しています。
抵抗R2を切り離すと、回路が途切れた状態となります。この状態が開放(オープン)です。
また、電流の流れやすさをインピーダンスといいます。インピーダンスが大きいほど電流が流れにくくなるのですが、回路が途切れている部分には電流が流れません。そのため、開放すると「インピーダンスが無限大になる」と表現することもあります。
開放前後の電流と電圧の大きさの変化

抵抗R2を『開放する前の状態』と『開放した後の状態』で回路に流れる電流IとA-B間の電圧VABを計算してみましょう。
抵抗R2を『開放する前の状態』
オームの法則より、回路に流れる電流Iは以下の値となります。
\begin{eqnarray}
I=\frac{V}{R_1+R_2}
\end{eqnarray}
また、A-B間の電圧VABは以下の値となります。
\begin{eqnarray}
V_{AB}=R_2V=\frac{R_2}{R_1+R_2}V
\end{eqnarray}
抵抗R2を『開放した後の状態』
抵抗R2を開放すると、インピーダンスが無限大となります。そのため、オームの法則より、回路に流れる電流Iは以下の値となります。
\begin{eqnarray}
I=\frac{V}{R_1+R_2}=\frac{V}{R_1+{\infty}}=0
\end{eqnarray}
上図に示している回路図の場合、抵抗R2を開放すると、回路に流れる電流Iがゼロとなります。そのため、抵抗R1での電圧降下がないため、電圧源の電圧VとA-B間電圧VABは同じになります。式で表すと以下のようになります。
\begin{eqnarray}
V_{AB}=V
\end{eqnarray}
以上より、『開放すると電流が流れなくなる』&『開放した箇所の電圧が大きくなる』ことが分かります。
スイッチがOFFの状態も開放という
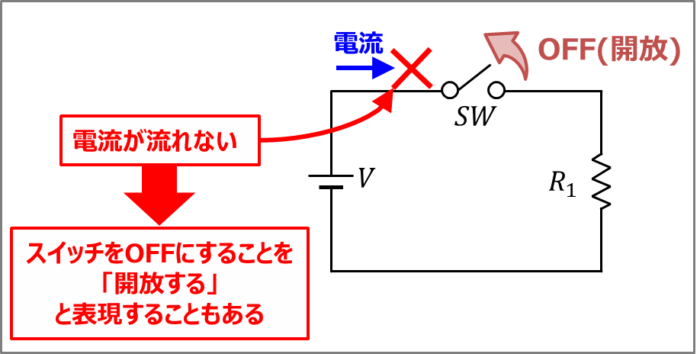
上図に電圧源V、スイッチSW、抵抗R1で構成されたシンプルな回路を示しています。スイッチSWをOFFにすると、回路の一部が途切れた状態となり、電流が流れなくなります。
そのため、スイッチをOFFにすることを「開放する」と表現することもあります。
短絡とは
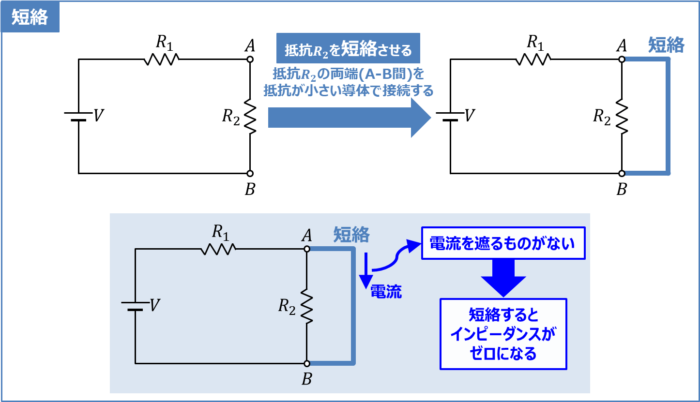
短絡とは、回路において電位差のある2点間を抵抗が小さい導体(電線など)で接続している状態のことを指します。短絡は『ショート』とも呼ばれています。
上図に電圧源V、抵抗R1、抵抗R2で構成されたシンプルな回路を示しています。この回路において、「抵抗R2を短絡させる」ということは「抵抗R2の両端(A-B間)を抵抗が小さい導体(電線など)で接続する」ということを意味しています。
短絡している部分では電流を遮るものがありません。そのため、短絡すると「インピーダンスがゼロになる」と表現することもあります。
短絡前後の電流と電圧の大きさの変化

抵抗R2を『短絡する前の状態』と『短絡した後の状態』で回路に流れる電流IとA-B間の電圧VABを計算してみましょう。
抵抗R2を『短絡する前の状態』
オームの法則より、回路に流れる電流Iは以下の値となります。
\begin{eqnarray}
I=\frac{V}{R_1+R_2}
\end{eqnarray}
また、A-B間の電圧VABは以下の値となります。
\begin{eqnarray}
V_{AB}=R_2V=\frac{R_2}{R_1+R_2}V
\end{eqnarray}
抵抗R2を『短絡した後の状態』
抵抗R2を短絡すると、抵抗R2の両端(A-B間)のインピーダンスがゼロとなります。そのため、オームの法則より、回路に流れる電流Iは以下の値となります。
\begin{eqnarray}
I=\frac{V}{R_1+R_2}=\frac{V}{R_1+0}=\frac{V}{R_1}
\end{eqnarray}
また、A-B間のインピーダンスRABがゼロなので、A-B間電圧VABはゼロとなります。式で表すと以下のようになります。
\begin{eqnarray}
V_{AB}=R_1V=0×I=0
\end{eqnarray}
以上より、『短絡すると電流が流れやすくなる』&『短絡した箇所は電圧がかからなくなる』ことが分かります。
短絡すると非常に大きな電流が流れるので注意
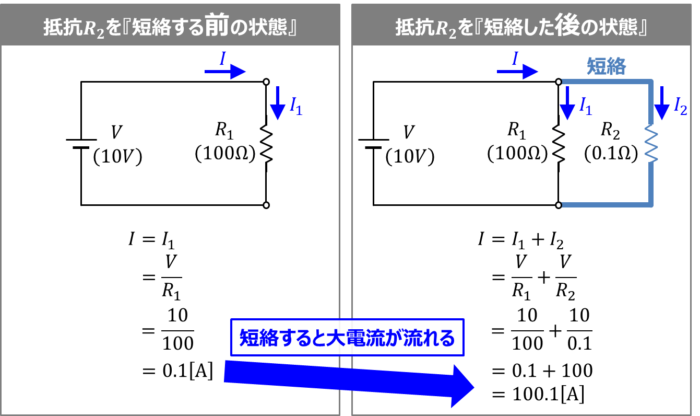
上図に電圧源V=10V、抵抗R1=100Ωで構成されたシンプルな回路を示しています。電流の大きさを決める抵抗が抵抗R1のみの場合を考えてみましょう。
抵抗R1を抵抗が小さい導体(抵抗値R2=0.1Ω)で『短絡する前の状態』と『短絡した後の状態』で回路に流れる電流Iを求めてみます。
抵抗が小さい導体(抵抗値R2=0.1Ω)で『短絡する前の状態』
オームの法則より、回路に流れる電流Iは抵抗R1に流れる電流I1と等しくなるため、以下の値となります。
\begin{eqnarray}
I=I_1=\frac{V}{R_1}=\frac{10}{100}=0.1{\mathrm{[A]}}
\end{eqnarray}
抵抗が小さい導体(抵抗値R2=0.1Ω)で『短絡した後の状態』
回路に流れる電流Iは抵抗R1に流れる電流I1と導体に流れる電流I2の合計になるため、以下の値となります。
\begin{eqnarray}
I=I_1+I_2=\frac{V}{R_1}+\frac{V}{R_2}=\frac{10}{100}+\frac{10}{0.1}=0.1+100=100.1{\mathrm{[A]}}
\end{eqnarray}
『短絡する前の状態』では回路に流れる電流Iは0.1A、『短絡した後の状態』では回路に流れる電流Iは100.1Aなので、回路を短絡すると非常に大きな電流が流れてしまうということが分かります。
なお、短絡時に流れる電流は『短絡電流』と呼ばれています。短絡電流が流れることによって、電線の被膜(電線を覆っている絶縁性の樹脂)が溶ける可能性があります。また、短絡時に火花が発生することで発火事故になるなど大きな問題を引き起こす可能性もあります。
まとめ
この記事では『開放』と『短絡』について、以下の内容を説明しました。
- 『開放』と『短絡』の違い
- 『開放』とは
- 『短絡』とは
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






